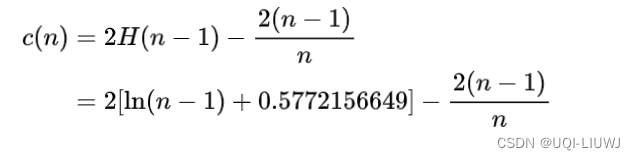1 异常类型
1.1 异常值outlier
给定输入时间序列,异常值是时间戳值其中观测值
与该时间序列的期望值
不同。
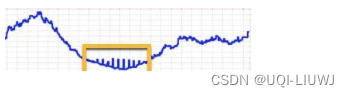
1.2 波动点(Change Point)
给定输入时间序列,波动点是指在某个时间t,其状态在这个时间序列上表现出与t前后的值不同的特性。
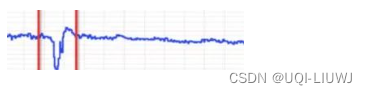
1.3 断层异常(Breakout)
时序系统中某一时刻的值比前一时刻的值陡增或者陡降很多,之后形态也发生了改变。

2 常见异常检测方法
2.1 基于统计
- 首先建立一个数据模型。异常是那些同模型不能完美拟合的对象
- eg,数据分布模型可以通过估计概率分布的参数来创建。如果一个对象不能很好地同该模型拟合,即如果它很可能不服从该分布,则它是一个异常
2.1.1 3σ法则
- 假如分布满足正态分布,那么 (μ−3σ,μ+3σ)区间内的概率为99.74。
- 所以可以认为,当数据分布区间超过这个区间时,即可认为是异常数据。

2.1.2 分位数异常检测
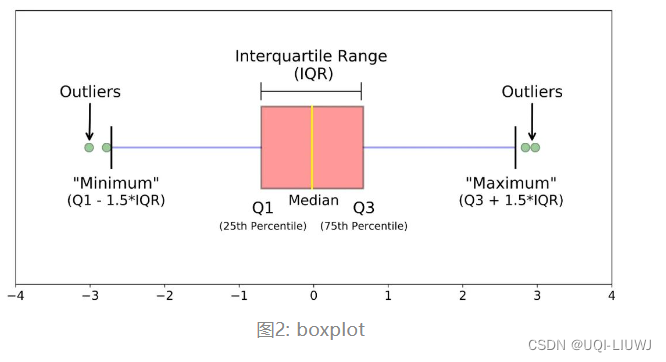
- IQR是第三四分位数减去第一四分位数,大于Q3+1.5*IQR之外的数和小于Q1-1.5*IQR的值被认为是异常值。
2.1.3 Grubbs测试
- 不断从样本中找出outlier的方法
- 这里的outlier,是指样本中偏离平均值过远的数据
-
算法流程
-
样本从小到大排序
-
求样本的mean和std
-
计算此时样本的min/max与mean的差距,距离更远的那个为可疑值
-
求可疑值的z-score (standard score),如果大于预先设定的Grubbs临界值,那么就是outlier;
-
对剩余序列不断做1~4步(每次检测一个异常点)
-
-
局限性:
-
它的判断机制是“逐一剔除”,所以每个异常值都要单独计算整个步骤,数据量大吃不消;
-
需假定数据服从正态分布或近正态分布。
-
2.2 基于预测
- 对于单条时序数据,根据其预测出来的时序曲线和真实的数据相比,求出每个点的残差
- 对残差序列建模,利用KSigma或者分位数等方法便可以进行异常检测

2.3 基于距离
2.3.1 k-最近邻
- 数据对象与最近的k个点的距离之和。
- 很明显,与k个最近点的距离之和越小,异常分越低;与k个最近点的距离之和越大,异常分越大。
- 设定一个距离的阈值,异常分高于这个阈值,对应的数据对象就是异常点。
2.4 基于密度的方法
2.4.1 Local Outlier Factor (LOF)
- 给每个数据点都分配一个依赖于邻域密度的离群因子 LOF,进而判断该数据点是否为离群点
- 好处在于可以量化每个数据点的异常程度(outlierness)
- 数据点p的局部相对密度(局部异常因子)为点p邻域内点的平均局部可达密度跟数据 点p的局部可达密度的比值(密度越小,越可能是异常点)
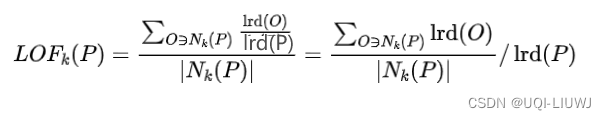
- 数据点P的局部可达密度=P最近邻的平均可达距离的倒数。距离越大,密度越小。
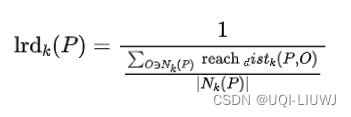
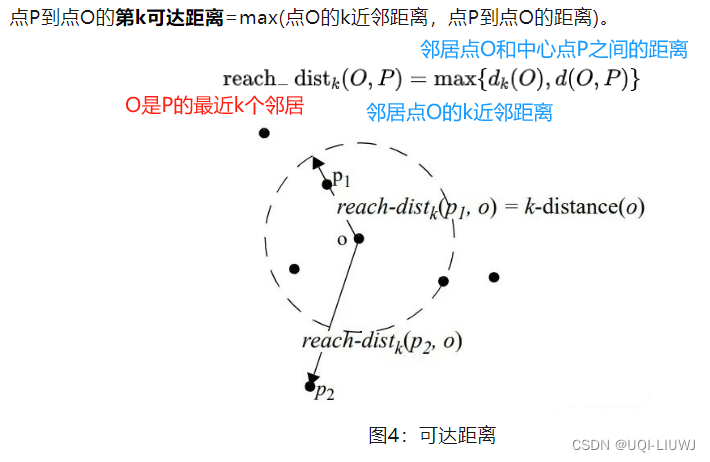
- 点O的k近邻距离=第k个最近的点跟点O之间的距离。
- 数据点P的局部可达密度=P最近邻的平均可达距离的倒数。距离越大,密度越小。
-
整体来说,LOF算法流程如下:
-
对于每个数据点,计算它与其他所有点的距离,并按从近到远排序;
-
对于每个数据点,找到它的K-Nearest-Neighbor,计算LOF得分。
-
2.5 基于聚类的方法
- 小于某个最小尺寸的所有簇视为异常
2.6 基于树的方法
2.6.1 孤立森林
- “孤立” (isolation) 指的是 “把异常点从所有样本中孤立出来”
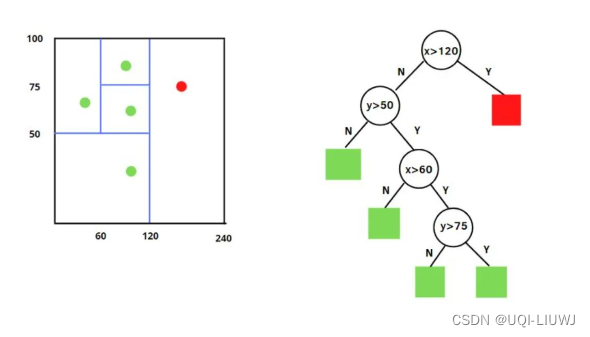
- 用一个随机超平面对一个数据空间进行切割,切一次可以生成两个子空间
- 接下来再继续随机选取超平面,来切割第一步得到的两个子空间
- 以此循环下去,直到每子空间里面只包含一个数据点为止
- ——>可以发现,那些密度很高的簇要被切很多次才会停止切割(每个点都单独存在于一个子空间内,才会停止切割);但那些分布稀疏的点,大都很早就停到一个子空间内了
- 孤立森林的算法思想:
- 异常样本更容易快速落入叶子结点
- 或者说,异常样本在决策树上,距离根节点更近
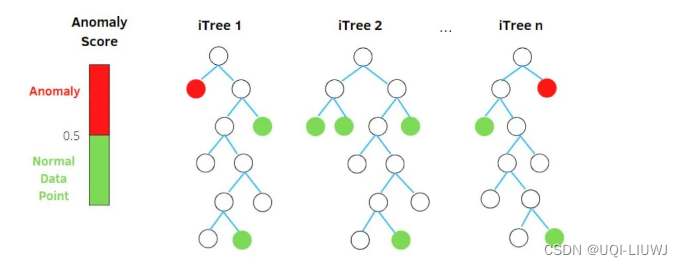
- 随机选择m个特征,通过在所选特征的最大值和最小值之间随机选择一个值来分割数据点。
- 观察值的划分递归地重复,直到所有的观察值被孤立。
- 获得 t 个孤立树后,单棵树的训练就结束了。接下来就可以用生成的孤立树来评估测试数据了,即计算异常分数 s。
- 对于每个样本 x,需要对其综合计算每棵树的结果(异常得分):
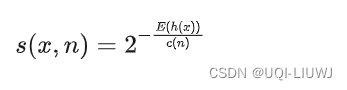
- E(h(x))——样本在这t棵孤立树上路径长度的均值
- c(n)——n个样本构建一个二叉搜索树BST中的末成功搜索平均路径长度
- 异常得分越大,平均路径长度越小,越容易是孤立点
- 对于每个样本 x,需要对其综合计算每棵树的结果(异常得分):
参考内容:【TS技术课堂】时间序列异常检测
时间序列异常检测综述