题目：

打印近似杨辉三角，行数n自选

百度找的杨辉三角，参考一下：

解析：

把它的全部元素左对齐，就可以看成近似杨辉三角的样子

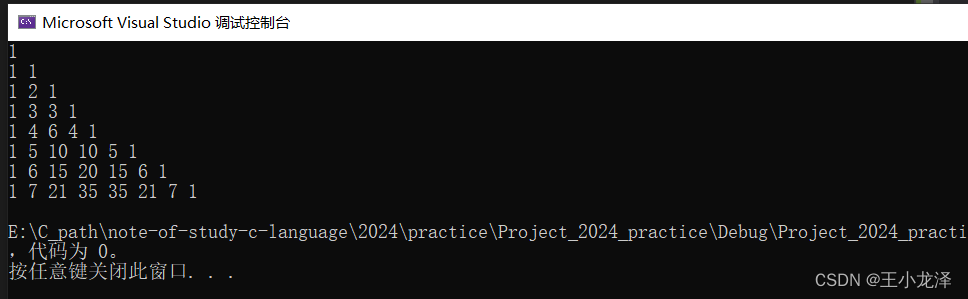
1

1  1

1  2  1

1  3  3  1

1  4  6  4  1

……

 每个数等于它上方两数之和

每行数字左右对称，由1开始逐渐变大

行数与列数相同，第n行有n列，首选二维数组，先给数组赋值，再打印数组

先搭元素为1的框架，每行第零列元素为1，每行末列元素为1

再根据每个数等于它上方两数之和，给其它元素赋值

逻辑：

先按规律给二维数组赋值，再打印所需数组元素

注意数组越界问题，N=n+2

参考代码：

// 打印杨辉三角，行数n自选
// 1// 1  1// 1  2  1// 1  3  3  1
// ……
#define n 7  // n:1~16
#define N n+2
#include<stdio.h>void init_arr(int arr[N][N])
{int i = 0;int j = 0;for (i = 1; i < N; i++){arr[i][1] = 1; // 每行第1列为1for (j = 2; j <=i; j++){arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];}}
}void print_arr(int arr[N][N])
{int i = 0;int j = 0;for (i = 1; i < N; i++){for (j = 1; j <= i; j++){printf("%d ", arr[i][j]);}printf("\n");}
}
int main()
{int arr[N][N] = { 0 };init_arr(arr);print_arr(arr);return 0;
}

运行结果：