🔗 运行环境:Matlab
🚩 撰写作者:左手の明天
🥇 精选专栏:《python》
🔥 推荐专栏:《算法研究》
🔐#### 防伪水印——左手の明天 ####🔐
💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗
💗今天分享matlab数学建模算法——模拟退火算法💗
📆 最近更新:2023 年 12 月 24 日,左手の明天的第 310 篇原创博客
📚 更新于专栏:matlab
🔐#### 防伪水印——左手の明天 ####🔐
目录
一、模拟退火算法
1 基本思想
2 基本步骤
二、算法流程
三、解决局部最优解
四、模拟退火算法在数学建模的应用
五、旅行商问题的matlab实现
1 旅行商问题
2 算法设计流程
(1)TSP问题的解空间和初始解
(2)新解的产生
(3)目标函数
(4)目标函数差
(5)Metropolis准则
3 matlab实现
六、MATLAB 模拟退火算法的示例代码
七、模拟退火算法优缺点
一、模拟退火算法
模拟退火算法(Simulated Annealing,SA)是一种模拟固体降温过程的最优化算法。其模拟的过程是首先将固体加温至某一温度,固体内部的粒子随温度上升慢慢变为无序的状态,内能增大,然后让其慢慢冷却,温度下降时,内部的粒子慢慢趋于有序,达到一种平衡态,最后达到常温时成为基态,此时内能减为最小。
模拟退火算法的基本原理分为三部分:初始解、解空间和目标函数。初始解是算法迭代的起点,试验表明,模拟退火算法是健壮的,即最终解的求得最优解并不十分依赖初始解的选取,从而可任意选择一个初始解。当然,如果初始解选择得当可以加快找到全局最优解。解空间一般是离散的可行解的集合。
1 基本思想
模拟退火算法的基本思想是将待求解的问题视为一个能量系统,系统的当前状态为解的状态,能量值为解的目标函数值,系统的状态转移依赖于Metropolis准则。

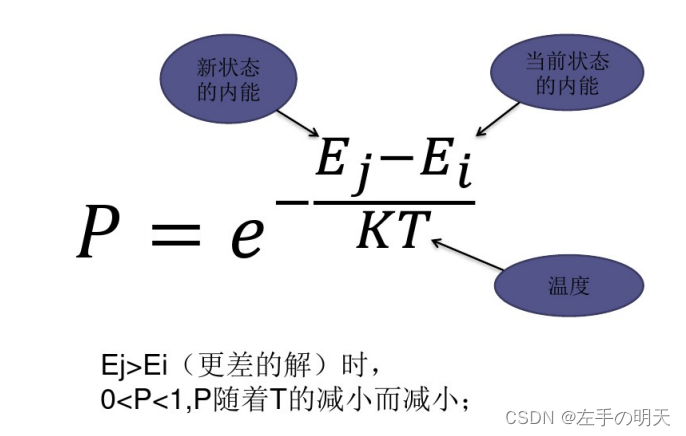
在模拟退火过程中,首先从某一初始解出发,将其视为系统的初始状态,然后通过随机选择不同的状态转移方式,不断迭代产生新的状态。在每一步转移中,根据目标函数值的差异和温度参数的大小,决定是否接受新状态作为当前状态。如果新状态的目标函数值更优,则一定概率上接受新状态;如果新状态的目标函数值更劣,则根据概率判断是否接受新状态。
模拟退火算法的精髓在于引入了温度参数,通过不断降低温度来引导系统从劣解逐步向最优解过渡。在这个过程中,通过Metropolis准则控制状态转移概率,使得算法在迭代过程中能够跳出局部最优解,向全局最优解靠近。
总的来说,模拟退火算法是一种基于概率的优化算法,通过模拟固体降温的过程,利用随机性和概率性寻找全局最优解,具有较好的鲁棒性和通用性。
2 基本步骤
模拟退火算法的基本步骤如下:
(1)初始化参数。包括初始温度、降温速率、终止温度和初始解等。
(2)产生新解。在当前解的邻域内产生一个新解。
(3)接受新解。计算当前解与新解之间的差异,如果新解更优,则接受它;否则,以一定的概率接受它。
(4)降温。根据设定的降温速率降低温度。
(5)终止判断。如果温度降低到终止温度以下,则停止搜索,输出最优解。
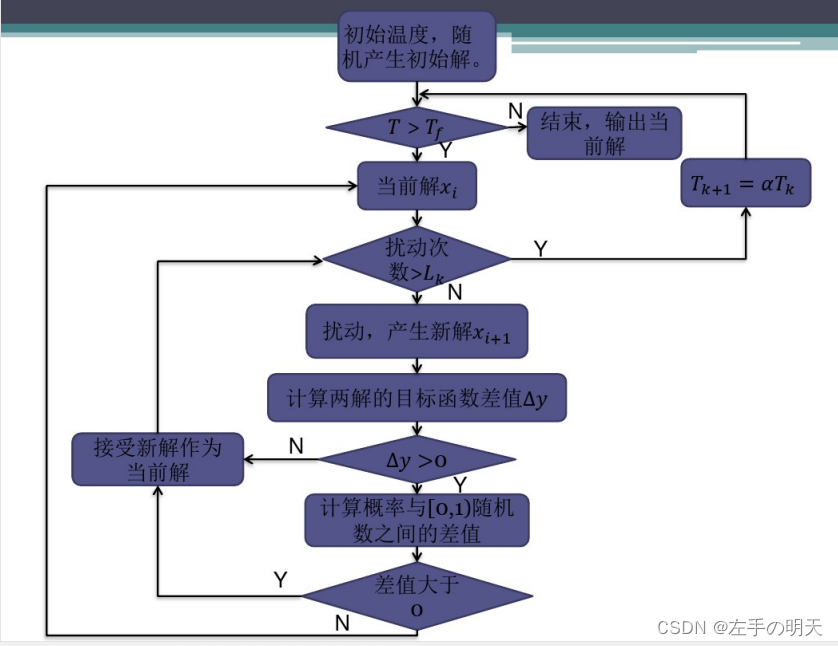
二、算法流程

三、解决局部最优解
模拟退火算法通过以下方式解决局部最优解的问题:
- 引入温度参数:模拟退火算法中的温度参数控制着算法的搜索过程。在高温状态下,算法更倾向于接受较差的解,这样可以探索更广阔的解空间;随着温度的降低,算法逐渐趋于保守,只接受更优的解。这种温度的变化过程有助于算法跳出局部最优解,向全局最优解过渡。
- Metropolis准则:模拟退火算法中的Metropolis准则是决定是否接受新状态的关键。当新状态比当前状态更优时,一定概率上接受新状态;当新状态更劣时,根据概率判断是否接受新状态。这样可以避免算法陷入局部最优解,而是通过概率的方式探索整个解空间。
- 随机性:模拟退火算法中的随机性使得算法在搜索过程中能够探索更多的解空间,而不是只停留在局部最优解附近。这种随机性有助于算法跳出局部最优解,向全局最优解靠近。
综上所述,模拟退火算法通过引入温度参数、Metropolis准则和随机性等方式,解决了局部最优解的问题。这种基于概率的优化算法能够跳出局部最优解,向全局最优解靠近,从而在各种优化问题中取得了较好的效果。
四、模拟退火算法在数学建模的应用
以下是模拟退火算法在数学建模竞赛中的一些应用场景:
- 旅行商问题(TSP):在这个经典问题中,模拟退火算法可以用来找到一条使得旅行商访问所有城市的总距离最短的路径。
- 背包问题:模拟退火算法可以用来解决背包问题,即在满足背包容量限制的前提下,找到一种物品组合使得背包中物品总价值最大。
- 图的着色问题:模拟退火算法可以用来解决图的最小着色问题,即给图的顶点分配最少的颜色,使得相邻的顶点颜色不同。
- 聚类问题:模拟退火算法可以用来解决数据聚类问题,即在给定数据集和聚类数量的前提下,找到一种聚类方式使得类内距离最小,类间距离最大。
- 车辆路径问题(VRP):模拟退火算法可以用来解决车辆路径问题,即在满足车辆容量和行驶距离限制的前提下,找到一种物品配送路径使得配送成本最小。
- 调度问题:模拟退火算法可以用来解决生产调度、车间调度等问题,目标是在满足生产约束的前提下,最小化生产时间、等待时间或者其他相关指标。
五、旅行商问题的matlab实现
1 旅行商问题
一名商人要到n个不同的城市去推销商品,每2个城市l和j之间的距离为d,如何选择一条路径使得商人每个城市走一遍后回到起点所走的路径最短。
例如:有52个城市,已知每个城市的坐标,求每个城市走一遍后回到起点,所走的路径最短。
2 算法设计流程
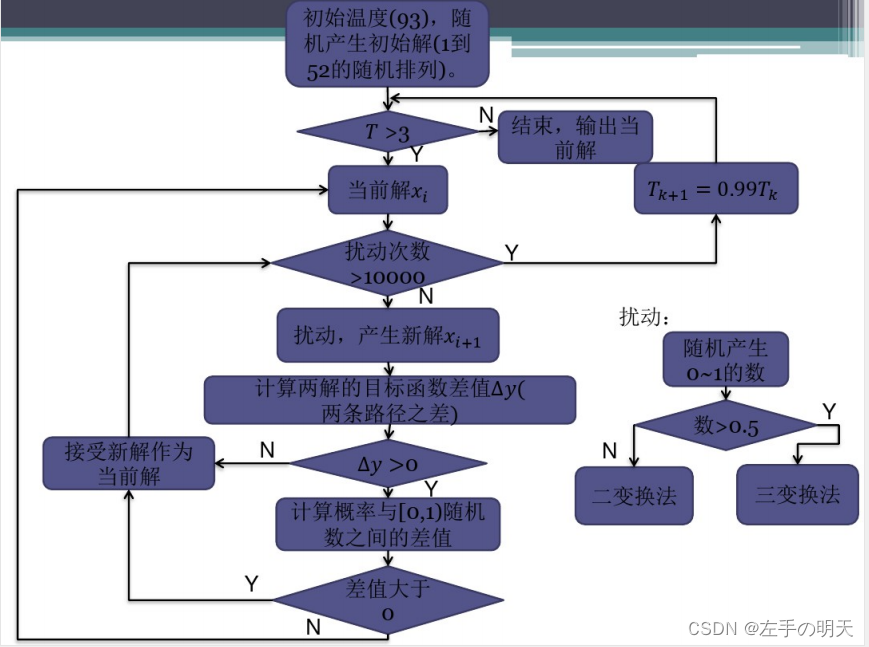
(1)TSP问题的解空间和初始解

(2)新解的产生
二变换法:任选序号u,v(设u<v<n),变换u,v之间的访问顺序
三变换法:任选序号u,v,w(设u<=v<w),将u,v之间的路径插到w之后访问
(3)目标函数

(4)目标函数差
计算变换前的解和变换后目标函数的差值:

(5)Metropolis准则
以新解与当前解的目标函数差定义接受概率,即
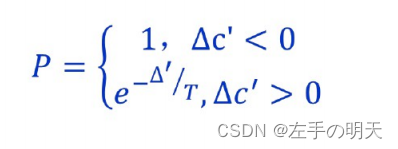
3 matlab实现
clear clca = 0.99; % 温度衰减函数的参数t0 = 97; tf = 3; t = t0;Markov_length = 10000; % Markov链长度coordinates = [
1 565.0 575.0; 2 25.0 185.0; 3 345.0 750.0;
4 945.0 685.0; 5 845.0 655.0; 6 880.0 660.0;
7 25.0 230.0; 8 525.0 1000.0; 9 580.0 1175.0;
10 650.0 1130.0; 11 1605.0 620.0; 12 1220.0 580.0;
13 1465.0 200.0; 14 1530.0 5.0; 15 845.0 680.0;
16 725.0 370.0; 17 145.0 665.0; 18 415.0 635.0;
19 510.0 875.0; 20 560.0 365.0; 21 300.0 465.0;
22 520.0 585.0; 23 480.0 415.0; 24 835.0 625.0;
25 975.0 580.0; 26 1215.0 245.0; 27 1320.0 315.0;
28 1250.0 400.0; 29 660.0 180.0; 30 410.0 250.0;
31 420.0 555.0; 32 575.0 665.0; 33 1150.0 1160.0;
34 700.0 580.0; 35 685.0 595.0; 36 685.0 610.0;
37 770.0 610.0; 38 795.0 645.0; 39 720.0 635.0;
40 760.0 650.0; 41 475.0 960.0; 42 95.0 260.0;
43 875.0 920.0; 44 700.0 500.0; 45 555.0 815.0;
46 830.0 485.0; 47 1170.0 65.0; 48 830.0 610.0;
49 605.0 625.0; 50 595.0 360.0; 51 1340.0 725.0;
52 1740.0 245.0;
];coordinates(:,1) = [];amount = size(coordinates,1); % 城市的数目% 通过向量化的方法计算距离矩阵dist_matrix = zeros(amount, amount);coor_x_tmp1 = coordinates(:,1) * ones(1,amount);coor_x_tmp2 = coor_x_tmp1';coor_y_tmp1 = coordinates(:,2) * ones(1,amount);coor_y_tmp2 = coor_y_tmp1';dist_matrix = sqrt((coor_x_tmp1-coor_x_tmp2).^2 + ...(coor_y_tmp1-coor_y_tmp2).^2);sol_new = 1:amount; % 产生初始解
% sol_new是每次产生的新解;sol_current是当前解;sol_best是冷却中的最好解;E_current = inf;E_best = inf; % E_current是当前解对应的回路距离;
% E_new是新解的回路距离;
% E_best是最优解的sol_current = sol_new; sol_best = sol_new; p = 1;while t>=tffor r=1:Markov_length % Markov链长度% 产生随机扰动if (rand < 0.5) % 随机决定是进行两交换还是三交换% 两交换ind1 = 0; ind2 = 0;while (ind1 == ind2)ind1 = ceil(rand.*amount);ind2 = ceil(rand.*amount);endtmp1 = sol_new(ind1);sol_new(ind1) = sol_new(ind2);sol_new(ind2) = tmp1;else% 三交换ind1 = 0; ind2 = 0; ind3 = 0;while (ind1 == ind2) || (ind1 == ind3) ...|| (ind2 == ind3) || (abs(ind1-ind2) == 1)ind1 = ceil(rand.*amount);ind2 = ceil(rand.*amount);ind3 = ceil(rand.*amount);endtmp1 = ind1;tmp2 = ind2;tmp3 = ind3;% 确保ind1 < ind2 < ind3if (ind1 < ind2) && (ind2 < ind3);elseif (ind1 < ind3) && (ind3 < ind2)ind2 = tmp3;ind3 = tmp2;elseif (ind2 < ind1) && (ind1 < ind3)ind1 = tmp2;ind2 = tmp1;elseif (ind2 < ind3) && (ind3 < ind1) ind1 = tmp2;ind2 = tmp3; ind3 = tmp1;elseif (ind3 < ind1) && (ind1 < ind2)ind1 = tmp3;ind2 = tmp1; ind3 = tmp2;elseif (ind3 < ind2) && (ind2 < ind1)ind1 = tmp3;ind2 = tmp2; ind3 = tmp1;endtmplist1 = sol_new((ind1+1):(ind2-1));sol_new((ind1+1):(ind1+ind3-ind2+1)) = ...sol_new((ind2):(ind3));sol_new((ind1+ind3-ind2+2):ind3) = ...tmplist1;end%检查是否满足约束% 计算目标函数值(即内能)E_new = 0;for i = 1 : (amount-1)E_new = E_new + ...dist_matrix(sol_new(i),sol_new(i+1));end% 再算上从最后一个城市到第一个城市的距离E_new = E_new + ...dist_matrix(sol_new(amount),sol_new(1));if E_new < E_currentE_current = E_new;sol_current = sol_new;if E_new < E_best
% 把冷却过程中最好的解保存下来E_best = E_new;sol_best = sol_new;endelse% 若新解的目标函数值小于当前解的,% 则仅以一定概率接受新解if rand < exp(-(E_new-E_current)./t)E_current = E_new;sol_current = sol_new;else sol_new = sol_current;endendendt=t.*a; % 控制参数t(温度)减少为原来的a倍enddisp('最优解为:')disp(sol_best)disp('最短距离:')disp(E_best)六、MATLAB 模拟退火算法的示例代码
以下是一个简单的 MATLAB 模拟退火算法的示例代码:
function [x_best, f_best] = simulated_annealing(f, lb, ub, init_temp, alpha, max_iter)
% SIMULATED_ANNEALING 模拟退火算法
% f: 目标函数
% lb: 变量的下界
% ub: 变量的上界
% init_temp: 初始温度
% alpha: 温度衰减系数
% max_iter: 最大迭代次数% 初始化
x = lb + (ub-lb).*rand(size(lb)); % 随机生成初始解
f_x = f(x); % 计算目标函数值
temp = init_temp; % 初始温度
x_best = x; % 最佳解
f_best = f_x; % 最佳目标函数值for iter = 1:max_iter% 生成新解x_new = x + randn(size(x)).*exp(-alpha.*temp); % 根据温度生成新解f_new = f(x_new); % 计算新解的目标函数值% 接受新解的准则if f_new < f_x || rand < exp(-alpha.*temp*(f_new-f_x))x = x_new; % 更新解f_x = f_new; % 更新目标函数值if f_x < f_best % 更新最佳解和最佳目标函数值x_best = x;f_best = f_x;endendtemp = max(temp - alpha, 0.01); % 温度衰减
end
end使用该函数的示例代码:
function y = f(x)
% 目标函数,这里选择简单的平方和函数 y = sum(x.^2)
y = sum(x.^2);
endlb = -10; % 变量的下界为 -10
ub = 10; % 变量的上界为 10
init_temp = 1000; % 初始温度为 1000
alpha = 0.95; % 温度衰减系数为 0.95
max_iter = 1000; % 最大迭代次数为 1000[x_best, f_best] = simulated_annealing(@f, lb, ub, init_temp, alpha, max_iter);
fprintf('最佳解:%f\n', x_best);
fprintf('最佳目标函数值:%f\n', f_best);七、模拟退火算法优缺点
模拟退火算法的优点包括:
- 通用性和简单性:模拟退火算法的实现比较简单,通用性强,适合解决各种不同类型的问题,尤其是一维和多维的优化问题。
- 概率保证性:模拟退火算法具有概率意义上的全局最优解,即对于一般的问题,它最终都能收敛到全局最优解,而不仅仅是局部最优解。
- 鲁棒性强:模拟退火算法对初始解的依赖性不强,因此对问题的敏感度较低,具有较强的鲁棒性。
- 能够有效避免局部最优解:通过引入随机因素,模拟退火算法能够跳出局部最优解,向全局最优解靠近。
然而,模拟退火算法也存在一些缺点:
- 计算量大:模拟退火算法需要进行大量的迭代和计算,尤其在问题规模较大时,计算量会显著增加,导致算法的运行时间较长。
- 对参数敏感:模拟退火算法的参数选择对其性能影响较大,如果参数选择不当,可能会导致算法性能不佳。
- 对某些问题收敛速度慢:对于一些复杂的问题,模拟退火算法可能需要较长时间才能收敛到全局最优解。
- 参数降温过程复杂:模拟退火算法中的降温过程需要精心设计,如果降温过程不合理,可能会导致算法性能不佳。
综上所述,模拟退火算法在解决各种优化问题时具有一定的优势和适用性,但也存在一些需要改进的方面。在实际应用中,需要根据具体问题选择合适的算法参数和实现方式,以获得最佳的优化效果。