创建时间:2024-02-04
最后编辑时间:2024-02-05
作者:Geeker_LStar
你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~
我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加油~!
⭐(●’◡’●) ⭐
那就让我们开始吧!
上两篇文章中,我详细讲了支持向量机(SVM)算法的原理,并用一个实例实现了它。在这一篇和下一篇中,我将分别讲解 & 实现朴素贝叶斯算法(分类器)。
上两篇传送门:
【初中生讲机器学习】3. 支持向量机(SVM)一万字详解!超全超详细超易懂!
【初中生讲机器学习】4. 支持向量机算法怎么用?一个实例带你看懂!
文章目录
- 一、五花八门的概率
- 先验概率
- 联合概率
- 条件概率
- 全概率公式
- 后验概率
- 二、贝叶斯公式
- 三、朴素贝叶斯算法
- 数学原理
- 分类
- 优缺点
一、五花八门的概率
嗯…概率论向来是一个令人头大的东西()可偏偏想要真正理解贝叶斯公式和朴素贝叶斯算法,概率是个绕不开的东西,并且它们的种类很多,有些又比较相似,还是很值得好好讲一下的。
以贝叶斯公式为出发,我们需要了解先验概率、联合概率、条件概率和后验概率。
先验概率
先验概率是对于某个独立事件,根据以往经验和分析得到的它可能发生/不发生概率。先验概率可记作 P ( C ) P(C) P(C)。
比如,你寒假前 25 天中有 5 天晚于 8:00 起床,那么你第 26 天晚于 8:00 起床的先验概率就是 20%。
联合概率
联合概率是两个或多个事件同时发生的概率,如果这些事件彼此独立,那么它们的联合概率等于它们之中每一个单独发生的概率的乘积(乘法原理)。但是如果彼此不独立,就不能这么用了,比如 “条件概率” 中讲到的小狗的例子。
联合概率可记作 P ( A ∩ B ) P(A∩B) P(A∩B) 或 P ( A , B ) P(A, B) P(A,B) 或 P ( A B ) P(AB) P(AB),如果 A、B 彼此独立,则 P ( A B ) = P ( A ) × P ( B ) P(AB) = P(A)×P(B) P(AB)=P(A)×P(B)。
从几何上看,联合概率就是下图中的交集部分。
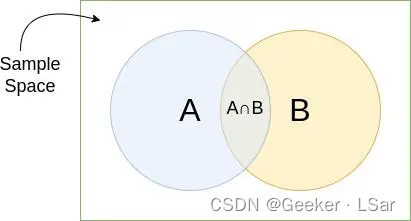
(先透露一句,朴素贝叶斯算法的 “朴素” 就和 “联合概率” and “彼此独立” 有关噢~)
比如,现在有两个均匀的骰子,一个蓝色一个红色,那么【投出蓝色的骰子且 6 点朝上】的概率就等于【投出蓝骰子的概率】×【6 点朝上的概率】,即 1 2 × 1 6 = 1 12 \frac{1}{2}×\frac{1}{6} = \frac{1}{12} 21×61=121。
条件概率
条件概率是指事件 A 在另外一个事件 B 已经发生的条件下的发生概率。
条件概率可记作 P ( A ∣ B ) P(A|B) P(A∣B),即 “在 B 条件下 A 发生的概率”,它等于 【B 发生且 A 发生的概率”】÷【B 发生的概率】,即 P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)。
从几何上来看,条件概率就是下图中的蓝色部分:
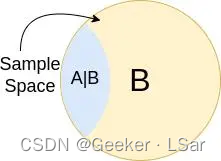
比如这道题:一种小狗由出生活到 5 岁的概率为 0.8,活到 10 岁的概率为0.4,问现年 5 岁的这种小狗活到 10 岁的概率是多少?
这很明显是个条件概率问题,即 “在活到 5 岁的条件下活到 10 岁的概率是多少”,由条件概率公式可得, P ( 10 岁 ∣ 5 岁 ) = P ( 活到 10 岁 ) P ( 活到 5 岁 ) = 0.4 0.8 = 0.5 P(10岁|5岁) = \frac{P(活到10岁)}{P(活到 5 岁)} = \frac{0.4}{0.8} = 0.5 P(10岁∣5岁)=P(活到5岁)P(活到10岁)=0.80.4=0.5,即这只小狗活到 10 岁的概率是 50%。
注意,由条件概率的定义可知, P ( A ∣ B ) ≠ P ( B ∣ A ) P(A|B) ≠ P(B|A) P(A∣B)=P(B∣A)。
另外,条件概率和联合概率一定要分清楚噢。一般情况下,条件概率是大于联合概率的,可以这么理解:联合概率中,事件 B 是未发生的,而在条件概率中,事件 B 已经发生,即 B 发生的概率是 1。或者去看这个例子:联合概率和条件概率到底有什么区别?
对之所以强调这个,就是因为我对着条件概率和联合概率的公式想了半天,这俩到底有啥不一样呢,后来终于搞懂了((
全概率公式
全概率公式的应用条件是:事件 B 1 、 B 2 、 B 3 … B k B_{1}、B_{2}、B_{3}…B_{k} B1、B2、B3…Bk 构成一个完备事件组且全部 P ( B i ) > 0 P(B_{i})>0 P(Bi)>0。简单来讲就是如果这 k k k 种情况能够覆盖全部情况(比如性别 “男” 和 “女”),那就能用全概率公式。
举个例子,一个人喜欢粉色的概率是多少?的答案等于 “这个人是男生且喜欢粉色的概率” 加上 “这个人是女生且喜欢粉色的概率”,比如 50 % ∗ 10 % + 50 % ∗ 80 % = 45 % 50\%*10\% + 50\%*80\% = 45\% 50%∗10%+50%∗80%=45%。这当中 “男生” 和 “女生” 就构成完备事件组,所用的公式就是全概率公式。
用数学语言表达一下,在上面所说的前提条件下有:
P ( A ) = ∑ i = 1 k P ( A ∣ B i ) × P ( B i ) P(A) = \sum\limits_{i=1}^{k}P(A|B_{i})×P(B_{i}) P(A)=i=1∑kP(A∣Bi)×P(Bi)
这就是全概率公式。
后验概率
对于后验概率的解释,比较好理解的是这一种:某件事已经发生,计算这件事发生的原因是由某个因素引起的概率。也就是说,后验概率是 “由果及因” 的。再换一种说法,如果条件概率是 P ( A ∣ B ) P(A|B) P(A∣B),即 “在 B 发生的条件下 A 发生的概率”,那么对应的后验概率就是 P ( B ∣ A ) P(B|A) P(B∣A),即 “在 A 发生的情况下,B 发生的概率是多少”。
举一个比较贴近人工智能的例子,我们现在已知 “如果这封邮件是垃圾邮件,那么邮件中出现某单词的概率是多少”,但是对于分类垃圾邮件的模型来说,更重要的肯定是 “如果这个单词出现了,那么这封邮件有多大概率是垃圾邮件”。这个 “更重要的” 就是后验概率。
很明显,后验概率都被称为 “后验” 了,那我们一开始肯定是不知道的,它是需要我们去求的。
所以,怎么求?
ok,这时候就要请我们大名鼎鼎的贝叶斯公式出场了!
二、贝叶斯公式
实不相瞒,贝叶斯公式是我最喜欢的公式之一,甚至有段时间我的 qq 个签都是它。
先用一句话概括一下贝叶斯公式在做什么:利用先验概率和条件概率计算出后验概率。
ok,那我们来推导一下,并且简单说一下贝叶斯公式通常用在什么地方。
其实贝叶斯公式的推导很简单。
我们要求 P ( B ∣ A ) P(B|A) P(B∣A),根据条件概率公式易得 P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A) = \frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB),又由 P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB) 变形可得 P ( A B ) = P ( A ∣ B ) × P ( B ) P(AB) = P(A|B)×P(B) P(AB)=P(A∣B)×P(B)。带回原式得到:
P ( B ∣ A ) = P ( A ∣ B ) P ( B ) P ( A ) P(B|A) = \frac{P(A|B)P(B)}{P(A)} P(B∣A)=P(A)P(A∣B)P(B)
yes!这就是贝叶斯公式~~它告诉我们一种【执果索因】的方法。这种方法在人工智能领域有广泛的应用。
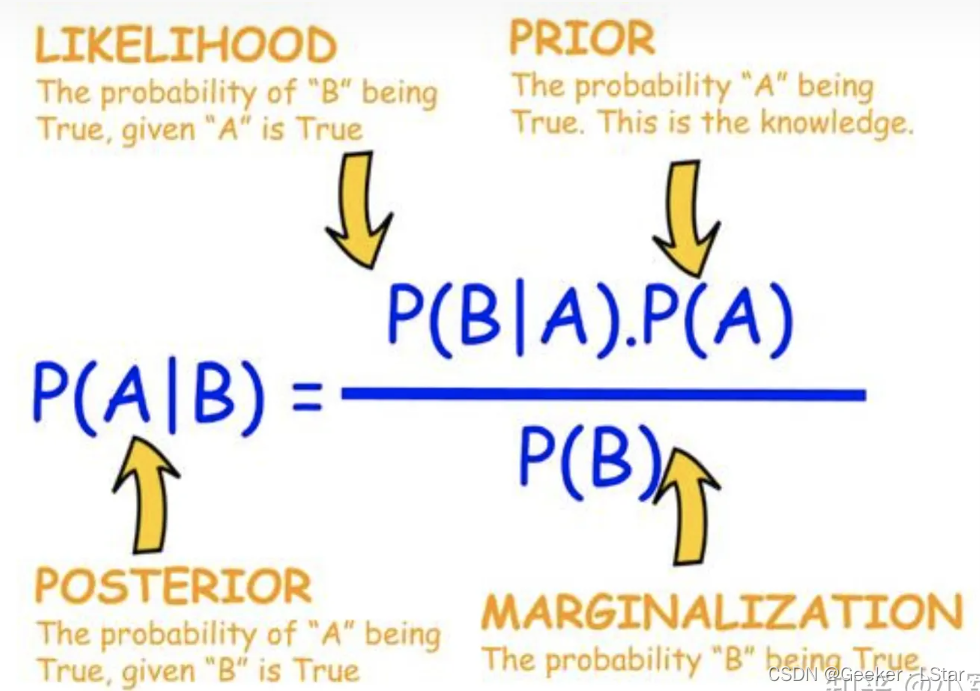
在贝叶斯公式众多的应用中,朴素贝叶斯算法是非常有名的一个。
三、朴素贝叶斯算法
和 SVM 不同,朴素贝叶斯算法是一种多分类算法,它广泛用于垃圾邮件过滤和文本分类当中。我们从贝叶斯公式出发,了解一下它的数学原理。
数学原理
来看一个例子:现在有一堆具有 m m m 个特征的样本和 k k k 个不同的分类 ( c 1 、 c 2 、 . . . 、 c k ) (c_{1}、c_{2}、...、c_{k}) (c1、c2、...、ck),某样本 X = [ x 1 、 x 2 、 . . . 、 x m ] X = [x_{1}、x_{2}、...、x_{m}] X=[x1、x2、...、xm],如何判断它属于这 K K K 个分类中的哪一个?
嗯,涉及到条件概率,这明显可以用贝叶斯公式解决,即:
P ( 类别 ∣ 特征 ) = P ( 特征 ∣ 类别 ) P ( 类别 ) P ( 特征 ) P(类别|特征) = \frac{P(特征|类别)P(类别)}{P(特征)} P(类别∣特征)=P(特征)P(特征∣类别)P(类别)
用语言表达就是:一个具有这些特征的样本属于某个分类的概率,等于【它具有这些特征且属于这个类别的概率】除以【它具有这个特征的概率】。——你别说,其实这逻辑还挺好理解的。
先来看分母, P ( 特征 ∣ 类别 ) × P ( 类别 ) P(特征|类别)×P(类别) P(特征∣类别)×P(类别)。
P ( 类别 ) P(类别) P(类别) 是先验概率,可以理解为:在不知道任何特征的情况下,这个样本属于某一类别的概率。比如,在 1000 组已知数据中(不考虑特征),属于 A 类别的有 800 个,属于 B 类别的有 150 个,属于 C 类别的有 50 个。那么,在给出一个新样本时(不考虑特征),它属于不同类别的概率就是 A 80%,B 15%,C 5%。
P ( 特征 ∣ 类别 ) P(特征|类别) P(特征∣类别) 是条件概率。朴素贝叶斯算法的 “朴素”,正是针对它而言的。
在日常生活中,一件事情或一个东西的各个特征之间或多或少都有一些关联(比如特征 “性别” 和特征 “喜欢的颜色”),几个特征彼此独立的情况是很少见的。BUT,特征之间彼此关联会极大地增加计算难度,而且其实我们也不知道某些特征之间的关联度到底有多少,这就很难办。
所以,为了解决这个问题,朴素贝叶斯算法假定, 所有特征之间是彼此独立的。 换言之,一个特征的改变并不会影响另一个特征的表现。
ok,这样的话我们就可以改写 P ( 特征 ∣ 类别 ) P(特征|类别) P(特征∣类别) 了。因为各个特征之间是彼此独立的,符合之前提到的那个联合概率计算公式的使用条件,即:
P ( 特征 ∣ 类别 ) = P ( 特征 1 ∣ 类别 ) × P ( 特征 2 ∣ 类别 ) . . . × P ( 特征 m ∣ 类别 ) P(特征|类别) = P(特征 1|类别)×P(特征 2|类别) ... ×P(特征 m|类别) P(特征∣类别)=P(特征1∣类别)×P(特征2∣类别)...×P(特征m∣类别)
这个公式挺好理解的,并不反直觉。写成数学表达式就是:
其中 Π \Pi Π 表示求积符号,连乘,类似于 Σ \Sigma Σ。
P ( 特征 ∣ 类别 ) = ∏ i = 1 m P ( 特征 i ∣ 类别 ) P(特征|类别) = \prod\limits_{i=1}^{m} P(特征 i|类别) P(特征∣类别)=i=1∏mP(特征i∣类别)
于是分子我们已经解决掉了,就是下面这个公式:
P ( 类别 ) × ∏ i = 1 m P ( 特征 i ∣ 类别 ) P(类别) × \prod\limits_{i=1}^{m} P(特征 i|类别) P(类别)×i=1∏mP(特征i∣类别)
接下来来看分母,分母只有一项 P ( 特征 ) P(特征) P(特征)。
根据上文讲过的全概率公式, P ( 特征 ) = P ( 特征 ∣ 类别 1 ) P ( 类别 1 ) + . . . + P ( 特征 ∣ 类别 k ) P ( 类别 k ) P(特征) = P(特征|类别 1)P(类别 1) +...+P(特征|类别 k)P(类别 k) P(特征)=P(特征∣类别1)P(类别1)+...+P(特征∣类别k)P(类别k),再加上刚刚讲过的,把 P ( 特征 ∣ 类别 ) P(特征|类别) P(特征∣类别) 用联合概率表示,最终的公式也就是:
P ( 特征 ) = ∑ j = 1 k P ( 类别 j ) × ∏ i = 1 m P ( 特征 i ∣ 类别 j ) P(特征) = \sum\limits_{j=1}^{k}P(类别 j)×\prod\limits_{i=1}^{m}P(特征 i|类别 j) P(特征)=j=1∑kP(类别j)×i=1∏mP(特征i∣类别j)
ok!我们现在已经顺利地将公式改写完成了!计算后验概率 P ( 类别 ∣ 特征 ) P(类别|特征) P(类别∣特征) 的公式如下:
P ( 类别 ∣ 特征 ) = P ( 类别 ) × ∏ i = 1 m P ( 特征 i ∣ 类别 ) ∑ j = 1 k P ( 类别 j ) × ∏ i = 1 m P ( 特征 i ∣ 类别 j ) P(类别|特征) = \frac{P(类别) × \prod\limits_{i=1}^{m} P(特征 i|类别)}{\sum\limits_{j=1}^{k}P(类别 j)×\prod\limits_{i=1}^{m}P(特征 i|类别 j)} P(类别∣特征)=j=1∑kP(类别j)×i=1∏mP(特征i∣类别j)P(类别)×i=1∏mP(特征i∣类别)
完美,这真是一个美妙的公式!
so,朴素贝叶斯公式要干什么呢?没错,它就是要根据上面这个公式求出一个已知特征的样本被分到不同类别的概率,其中概率最大的类别就是这个样本最终被分到的类别。
综上,朴素贝叶斯分类器可以表示为:
f ( x ) = a r g m a x P ( 类别 ∣ 特征 ) = a r g m a x P ( 类别 ) × ∏ i = 1 m P ( 特征 i ∣ 类别 ) ∑ j = 1 k P ( 类别 j ) × ∏ i = 1 m P ( 特征 i ∣ 类别 j ) f(x) = argmax P(类别|特征) = argmax \frac{P(类别)×\prod\limits_{i=1}^{m} P(特征 i|类别)}{\sum\limits_{j=1}^{k}P(类别 j)×\prod\limits_{i=1}^{m}P(特征 i|类别 j)} f(x)=argmaxP(类别∣特征)=argmaxj=1∑kP(类别j)×i=1∏mP(特征i∣类别j)P(类别)×i=1∏mP(特征i∣类别)
不难发现,对于同一个样本,分母总是一样的,因为分母就是 P ( 特征 ) P(特征) P(特征)(同一个样本的特征肯定是一样的)。把分母去掉后,朴素贝叶斯分类器最终表示为:
f ( x ) = a r g m a x P ( 类别 ) × ∏ i = 1 m P ( 特征 i ∣ 类别 ) f(x) = argmax P(类别) × \prod\limits_{i=1}^{m} P(特征 i|类别) f(x)=argmaxP(类别)×i=1∏mP(特征i∣类别)
这就是朴素贝叶斯分类器的计算原理!其实最后真正用于计算的就是 P ( 特征,类别 ) P(特征,类别) P(特征,类别),也就是联合概率!
只能说,妙哉。
emmm but,现在有另一个小问题。在这个公式中,如果其中一项比如 P ( 特征 2 ∣ 类别 ) P(特征 2|类别) P(特征2∣类别) 为 0,会导致整个式子都变成 0,这显然不合理。
为了避免这样的情况,我们可以使用拉普拉斯平滑,这是一种常用的平滑方法,通过避免零概率问题来提高分类器的准确率。
拉普拉斯平滑简单来说就是在分子分母上同时加一个不为 0 的数,在样本量很大的时候,这种操作一般对结果造不成什么影响。
比如,上文公式中的 P ( 类别 ) = 已知数据中被分到该类别的样本数 D y 样本总数 D P(类别) = \frac{已知数据中被分到该类别的样本数 D_{y}}{样本总数 D} P(类别)=样本总数D已知数据中被分到该类别的样本数Dy,运用拉普拉斯平滑,变为 D y + 1 D + N \frac{D_{y}+1}{D+N} D+NDy+1,其中 N N N 为总类别数。
类似的, P ( 特征 i ∣ 类别 ) P(特征 i|类别) P(特征i∣类别) 用拉普拉斯平滑可以表示为 D y , 特征 i + 1 D y + N i \frac{D_{y, 特征 i}+1}{D_{y}+N_{i}} Dy+NiDy,特征i+1, N i N_{i} Ni 表示特征 i i i 可能的取值数。
当然,分子上不一定要加 1,可以加任意数 x x x,但是分母需要对应的加上 μ x μx μx,其中 μ μ μ 对应分子可能的种类数。
经过这么一番操作,朴素贝叶斯算法的准确率就更高了。
分类
和 SVM 一样,朴素贝叶斯算法也分为几种,每种负责处理不同类型的问题。
- 高斯模型
高斯模型负责处理连续型数据,比如人的身高。
一些连续型数据虽然可以转化为离散型数据(如身高在 150-160 之间用 1 代表),但是这样必然会导致精度不足,使用高斯模型可以避免这个问题。
对于离散型数据,可以使用多项式模型或伯努利模型。
- 多项式模型
多项式模型的使用最为广泛。比如统计某文档中的单词,如果直接以单词出现的频次计算,可以使用多项式模型。 - 伯努利模型
伯努利模型的适用情况非常鲜明——当数据可以用布尔类型表示的时候,即全为 1 或 0,全为 true or false。还是统计单词的例子,如果按照单词是否出现(1、0)来统计,可以使用伯努利模型。
优缺点
以下是朴素贝叶斯算法的优缺点:
- 优点:
- 以贝叶斯公式为基础,具有稳定的分类效率
- 算法逻辑简单,计算开销小,适合增量式训练,即使在数据量超出内存时也能分批次进行。
- 能够处理多分类任务。
- 对缺失数据不敏感:当数据中有缺失值时,朴素贝叶斯算法可能比其它算法表现更好。
- 缺点:
- 依赖 “所有特征彼此独立” 的假设,但这种假设在实际情况中不太可能成立。
- 基于先验概率,如果先验概率偏差较大,对模型的分类效果影响大。
- 对输入数据的表达形式敏感:离散、连续、极大极小值等,若输入数据的表达形式与假设不符,对模型分类效果影响较大。
以上,我们对朴素贝叶斯算法已经有了一个比较详细的了解啦!!!
ok!!!!!以上就是关于朴素贝叶斯算法的详细讲解!!
嘿嘿真的非常开心你能够看到这里!!一起加油!
如果有任何 bug 欢迎评论区拷打我!!
这篇文章从概率开始,详细地讲了贝叶斯公式和朴素贝叶斯算法,希望对你有所帮助!⭐
——Geeker_LStar
![[C++]继承(续)](https://img-blog.csdnimg.cn/direct/362d3f06ef344ae4be6a0042dead03a1.png)