本文摘要

本文叙述了对股票市场高频数据分析一个简单方法，即已实现波动率的计算和后续的相关研究。
采用上证综指2019年至2021年3年间实时交易价格的每分钟数据，在已实现方差法下计算了各抽样频率下上证综指日已实现波动率的数值(Realized Volatility，以下简称RV)，分析了上证综指在不同抽样频率下计算得到的RV之间的统计特征与关联。

研究背景

波动率的种类多种多样，如历史波动率、实际波动率，隐含波动率等等，在诸多的形形色色的波动率种类中，有一种波动率独树一帜，其以可以准确描绘股市微观结构，充分反映股市波动信息而备受关注，即已实现波动率(Realized Volatility)，其由Merton(1980)基于日内高频数据提出这一全新的概念。已实现波动率是由日内高频数据计算得出的，在充分利用了日内交易信息的同时，包含了日内收益率变化的全部信息，因此在理论上可以使波动率的估计更加准确。

已实现波动率的计算

什么是已实现波动率

已实现波动率衡量的是股票价格在一天内波动的剧烈情况

计算原理

本文的计算RV的方法如下：对于第$t$个交易日，整个交易时间段记为[0,1]，将其分成$n=1/\Delta$($\Delta$为采样频率)个子区间，RV 被定义为该日所有高频收益率的平方和：
$R{V}_t={\sum }_{i=1}^{1/\Delta }{r}_{t,i}^2$
其中$r_{t,i}$是第$t$天第$i$个交易间隔内的对数收益率，按照以下公式计算：
$r_{,i}=ln{P}_{t,i}-ln{P}_{t,i-1}$
式中，$P_{t,i}$为上证指数在$t$日$i$时刻的收盘价，$P_{t,i-1}$为上证指数在$t$日$i$时刻的前一个时刻的收盘价，$t$取样本中交易日。

代码实现

首先要导入使用的相关包

# -*- coding: utf-8 -*-
"""
Created on Thu Apr 21 19:59:23 2022
@author: Tang
@e-mail: tang20200924@163.com
"""import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import math

读入原始高频数据数据（本文使用的高频数据原始数据见作者上传的下载文件包）

#读入excel文件
filepath1 = r"C:\Users\admin\Desktop\上证综指\2019.xlsx"
df1 = pd.read_excel(filepath1)  
filepath2 = r"C:\Users\admin\Desktop\上证综指\2020.xlsx"
df2 = pd.read_excel(filepath2)  
filepath3 = r"C:\Users\admin\Desktop\上证综指\2021.xlsx"
df3 = pd.read_excel(filepath3)  

将读到的三个数据文件整合到一起，同时由于上证综合指数高频数据不是一般股票交易数据，其交易时间从9点到下午3点半之间都有，而且是不规则的，这里还需要对9点半和下午3点后的数据去除，中午休市的时候价格不变动，因此不影响计算结果。
去除方法是引入“时间戳”。

#合并3年数据
df=pd.concat([df1,df2,df3])#改写列名
new_col = ['date', 'time' ,'close']
df.columns = new_col#引入时间数据
df['time'] = pd.to_datetime(df['time'])
#清洗数据
df=df[(df['time'] >=pd.to_datetime('09:30:00')) & (df['time'] <= pd.to_datetime('15:00:00'))]

可以看到，在生成df数据集里，有20余万条数据，包含730个交易日，为了计算每天的数值，是个非常繁琐的过程，我们这里采用groups语句来处理。

#按日期分割
groups = df.groupby(df.date)

这个语句的作用是将df数据集按照天数分割成了730个小数据集储存在groups里，后面我们用循环语句调用即可：

"""计算RV_1min"""
RV_1min = []
for i,group in groups:group["close_lag"] = group["close"].shift(1)group["ln_clo"] = group["close"].apply(np.log) group["ln_clo_lag"] = group["close_lag"].apply(np.log) group["r"]=group["ln_clo"]-group["ln_clo_lag"]group["r^2"]=group["r"]*group["r"]rv = group['r^2'].sum()  RV_1min.append(rv)

这里计算的是以一分钟抽样频率计算的已实现波动率，同理修改参数我们也可以计算5分钟抽样频率的，一般认为1分钟抽样频率过高，5分钟或10分钟的抽样频率可以很好的平衡微观结构噪声和保持信息的不丢失。

"""计算RV_5min """ 
RV_5min = []
#计算RV_5min    
for i,group in groups:#获取抽取序列a=[]for i in range(0,len(group),5):#每隔5行取数据a.append(i) group=group.iloc[a] group["close_lag"] = group["close"].shift(1)group["ln_clo"] = group["close"].apply(np.log) group["ln_clo_lag"] = group["close_lag"].apply(np.log) group["r"]=group["ln_clo"]-group["ln_clo_lag"]group["r^2"]=group["r"]*group["r"]rv = group['r^2'].sum()  RV_5min.append(rv)    

剩下10分钟和30分钟的代码同样，不再展示。接下来将生成的结果汇总保存，已备后文分析。

"""生成最终数据"""
date=df[["date"]]#提取日期
date.drop_duplicates(subset=None, keep='first', inplace=True)#删除重复日期 
date=date.reset_index(drop=True)#重置索引以拼接#将list转换为dataframe以绘图  
RV_1 = pd.DataFrame([RV_1min],index=["RV_1min"])
RV_5 = pd.DataFrame([RV_5min],index=["RV_5min"])
RV_10 = pd.DataFrame([RV_10min],index=["RV_10min"])
RV_30 = pd.DataFrame([RV_30min],index=["RV_30min"])#转置
RV_1_2 = RV_1.T
RV_5_2 = RV_5.T
RV_10_2 = RV_10.T
RV_30_2 = RV_30.T#生成最终RV数据集
RV_SZ=pd.concat([date,RV_1_2,RV_5_2,RV_10_2,RV_30_2],axis=1)   

保存数据

"""保存数据
writer = pd.ExcelWriter(r"C:\Users\admin\Desktop\上证RV.xlsx")
RV_SZ.to_excel(writer, "sheet1")
writer.save()
"""

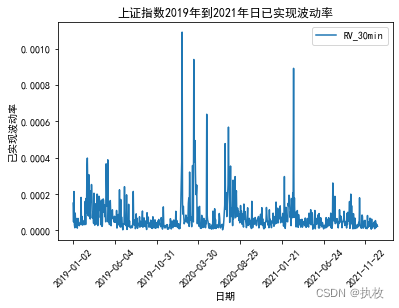
我们来绘图看下结果

"""绘图"""
plt.rcParams['font.sans-serif'] = ['simhei'] #字体为黑体
plt.rcParams['axes.unicode_minus'] = False #正常显示负号 #时序图的绘制
RV_SZ.plot("date","RV_30min",kind = 'line')#这是绘图函数
plt.xticks(rotation=45) #坐标角度旋转
plt.xlabel('日期') #横、纵坐标以及标题命名
plt.ylabel('已实现波动率')
plt.title('上证指数2019年到2021年日已实现波动率',loc='center')

接下来的几篇文章将对RV进行分析，包括统计性描述，ARIMA模型，EGARCH模型等等。