方式一
npm install axios
在$NODE_PATH/node_modules/axios/dist路径下即可找到axios.js。

方式二
1、百度搜索 GitHub 官网:https://github.com/
2、搜索 axios
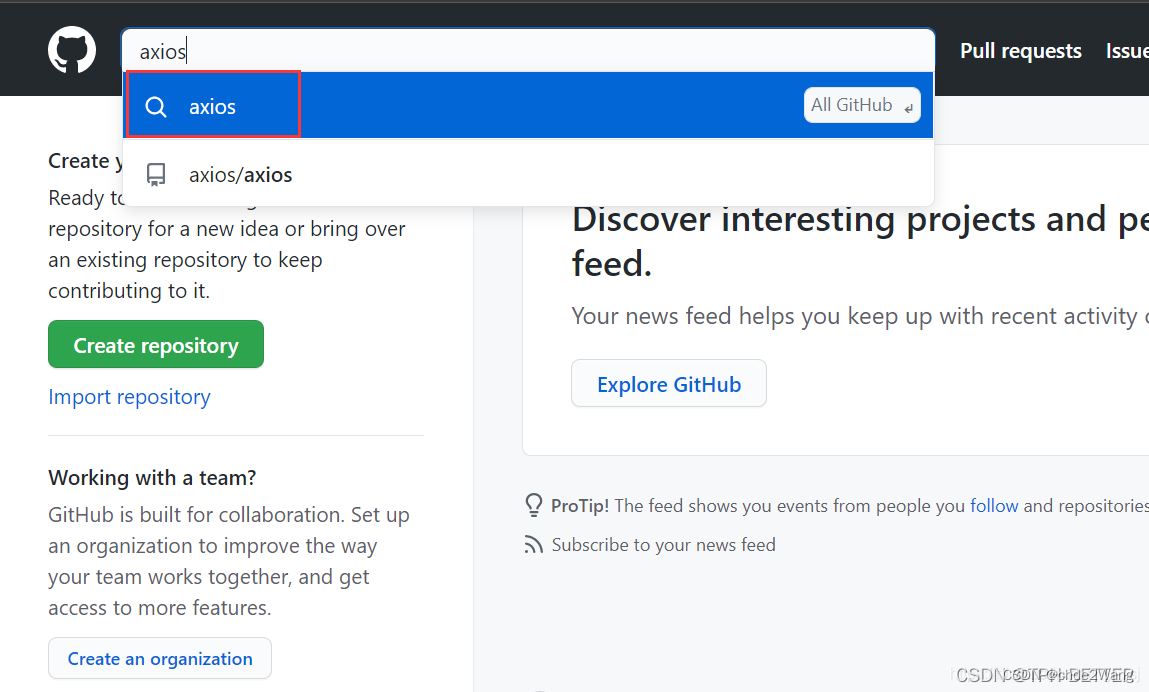
3、点击 axios/axios
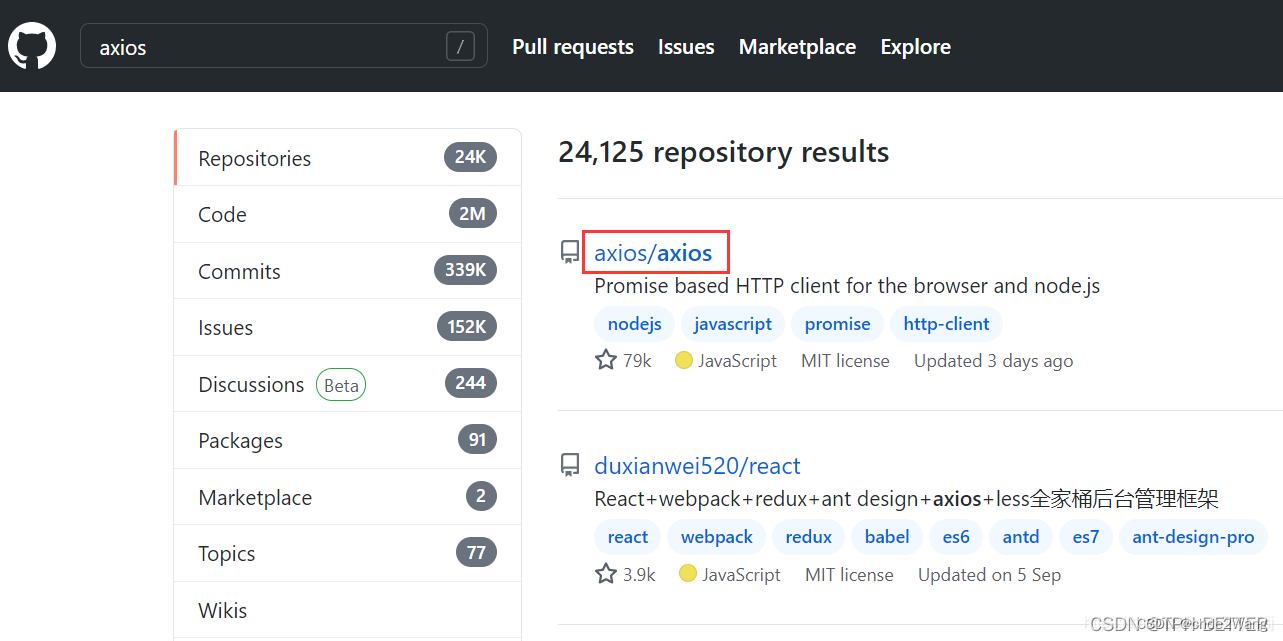
4、下载到本地
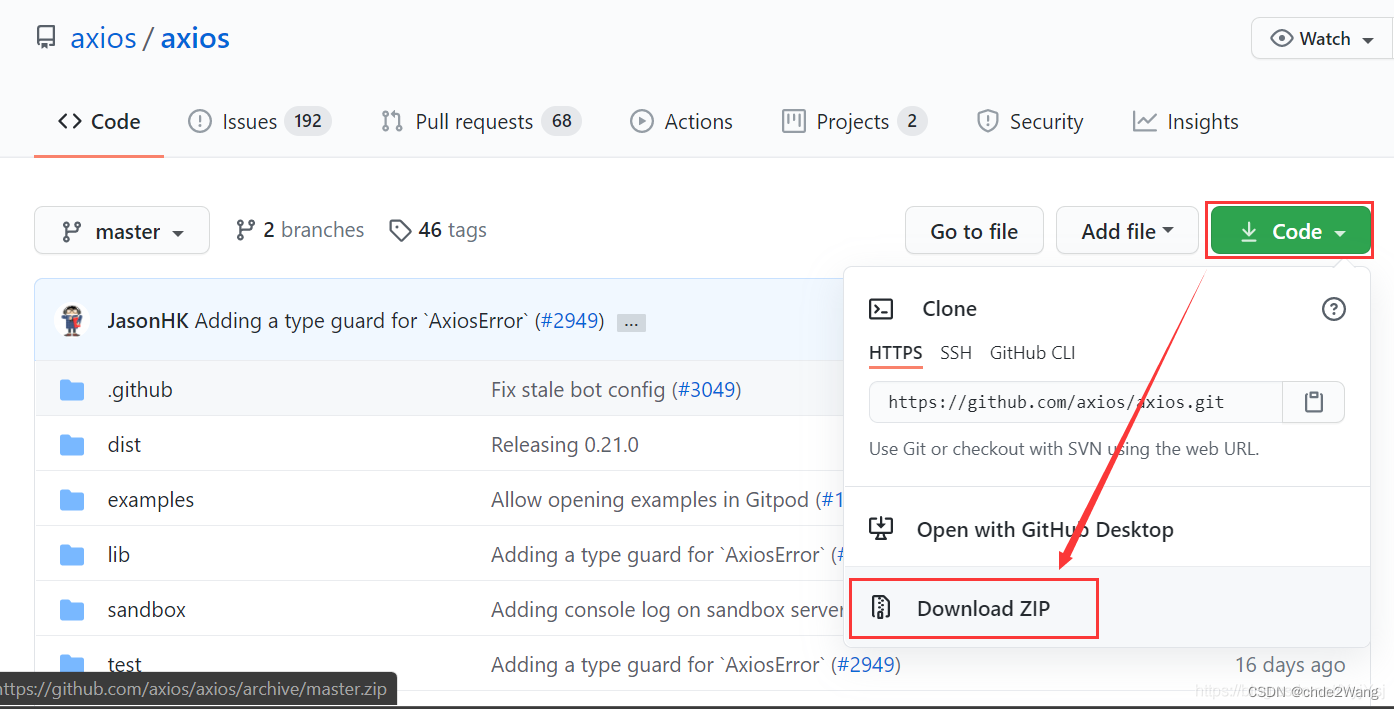
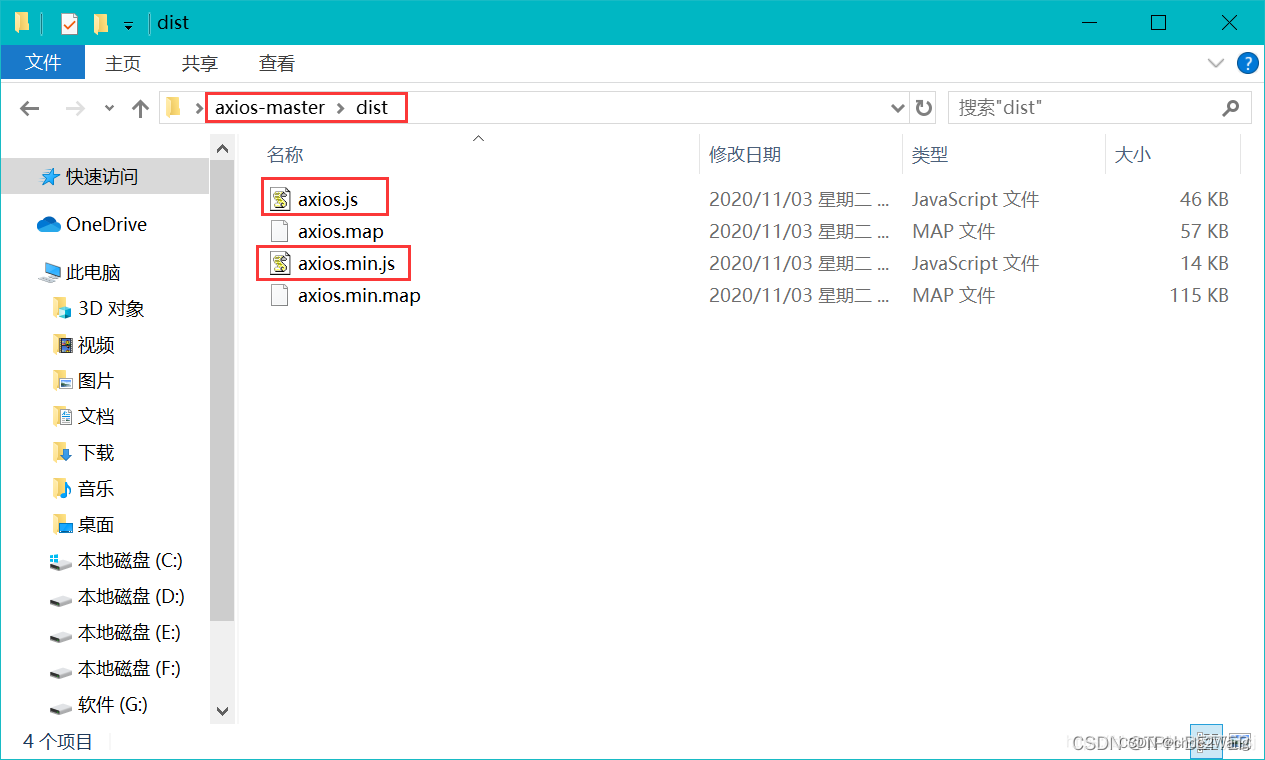
5、解压,进入到 dist 文件夹**
参考:https://blog.csdn.net/weixin_46055693/article/details/122961451?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-122961451-blog-123159813.235v43pc_blog_bottom_relevance_base5&spm=1001.2101.3001.4242.1&utm_relevant_index=3