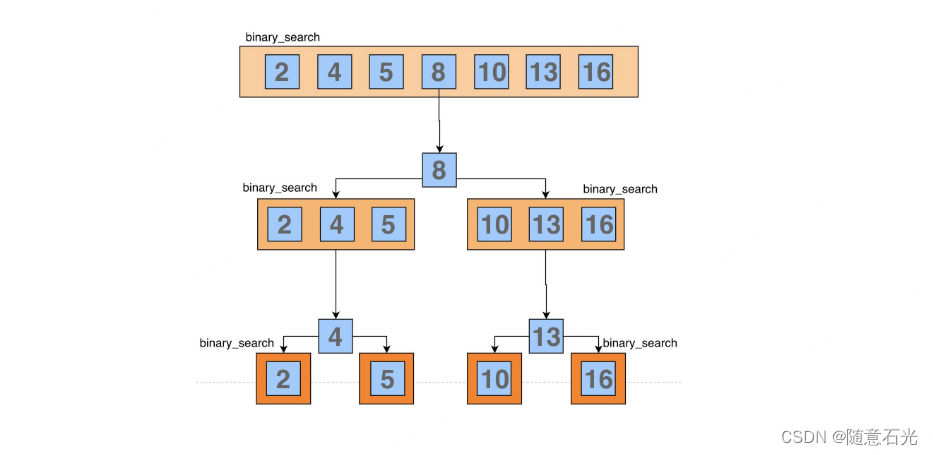
前缀和
题目
输入一个长度为 n的整数序列。
接下来再输入 m个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n和 m。
第二行包含 n个整数,表示整数数列。
接下来 m行,每行包含两个整数 l和 r,表示一个询问的区间范围。
输出格式
共 m行,每行输出一个询问的结果。
求解
可以先用一个数组sum存储从0到i位置的前缀子列和。
sum[i] = sum[i-1]+a[i]
对于从第 l 个数到第 r 个数的和,可写作sum[r] - sum[l-1]
#include <iostream>using namespace std;int n, m;
int q[100010];
int sum[100010];void addsum(int q[], int n){int i =0;sum[0] = 0;for(i =1; i<=n ;i++){sum[i] = sum[i-1] + q[i-1];}
}int main(){cin>>n>>m;int i ;int start, end;for(i =0 ;i<n;i++){cin>>q[i];}addsum(q, n);for( i =0; i<m; i++){cin>>start>>end;cout<<sum[end] - sum[start-1]<<endl;}return 0;}
子矩阵的和
输入一个 n行 m列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n行,每行包含 m个整数,表示整数矩阵。
接下来 q行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q行,每行输出一个询问的结果。
思路:
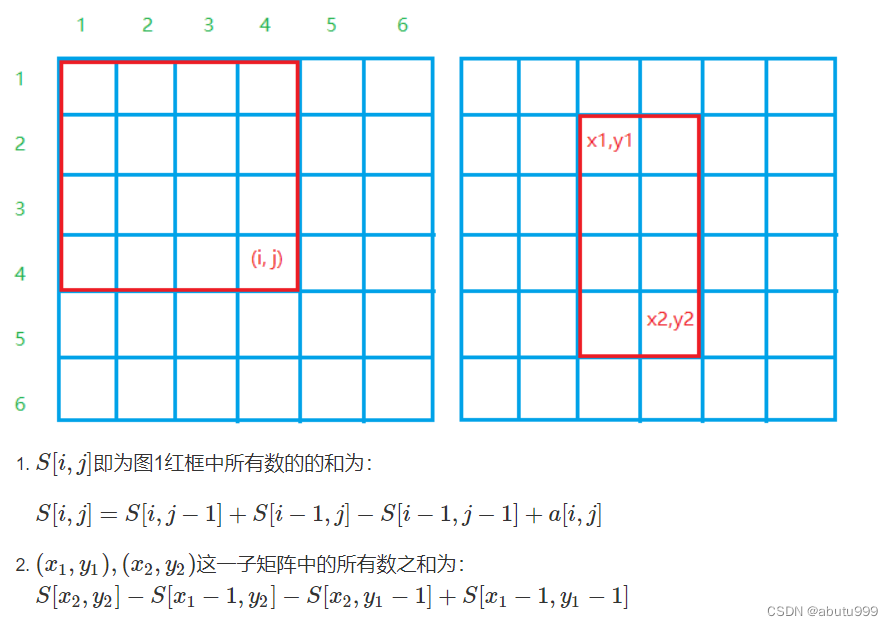
#include <iostream>using namespace std;int n, m;
int q[1001][1001];
int qu;
int s[1001][1001];int main(){cin>>n>>m;cin>>qu;int i,j;for(i =0 ; i< n;i++){for(j =0 ; j< m; j++){cin>>q[i][j];}}s[1][1] = q[0][0];for(i =1 ; i<= n;i++){for(j =1 ; j<= m; j++){s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + q[i-1][j-1];//cout<<s[i][j]<<endl;}}int x1,y1,x2,y2;for( i =0 ; i<qu ;i++){cin>>x1>>y1>>x2>>y2;//cout<<s[x2][y2]<<" "<< s[x1-1][y2]<<" "<<s[x2][y1-1] <<" "<<s[x1-1][y1-1]<<endl;cout<<s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]<<endl;}}
差分
输入一个长度为 n的整数序列。
接下来输入 m个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r]之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n和 m。
第二行包含 n个整数,表示整数序列。
接下来 m行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n个整数,表示最终序列。
思路:
对原数组a构造差分数组b

试想 对从位置l开始到r的数组统统加c,直接循环需要(r-l+1)次
如果我们对其差分数组进行操作
b[l]+c后, 其原数组从i开始往后的所有数组都+c
b[r+1]+c后, 其原数组从r+1开始往后的所有数组都-c
所以。我们可以直接转换为
b[l]+= c;
b[r+1]-=c;
#include <iostream>using namespace std;int n;
int m;
int q[100001];
int b[100001];int main(){cin>>n>>m;int i ;for(i=1; i<=n; i++){cin>>q[i];}for(i=1; i<=n ;i ++){b[i] = q[i] - q[i-1];}int l, r,c;for(i =0; i<m ;i++){cin>>l>>r>>c;b[l]+= c;b[r+1]-=c;}for(i=1; i<=n; i++){q[i] = q[i-1] + b[i];cout<<q[i]<<" ";}}