✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty‘s blog

前言

在上一章节中我们讲解了数据结构中的顺序表，知道了顺序表的空间是连续存储的，这与数组非常类似，为我们随机访问数据提供了便利的条件。但是同时当插入数据时可能存在移动数据与扩容的情况，这大大增加我们的时间与空间成本。为了解决这个问题，就要学习我们今天要讲解的链表。

1. 什么是链表

链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。与顺序表不同，链表的存储数据在内存是随机分布的。

2. 链表的分类

链表的种类多种多样，其中最常见的有八种，它们大致可以分为三类：

2.1 单向或者双向

2.2 带不带头节点

2.3 循环不循环

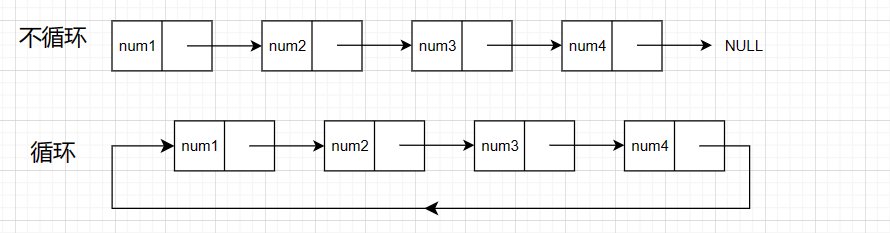
本专栏将选择其中两种常见链表进行讲解，那就是无头单向非循环链表与与带头双向循环链表，这两种优点主要有：

• 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
• 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带来很多优势，实现反而简单了，后面我们代码实现了就知道了。

3. 单链表的功能

单链表的主要功能有以下几个：

1. 打印单链表中的数据。
2. 对单链表进行头插(开头插入数据)。
3. 对单链表进行头删(开头删除数据)。
4. 对单链表进行尾插(末尾插入数据)。
5. 对单链表进行尾删(末尾删除数据)。
6. 对单链表进行查找数据。
7. 对单链表数据进行修改。
8. 任意位置的删除和插入数据。
9. 销毁单链表。

4. 单链表的定义

单链表的结点定义方式与我们以往定义的方式都不同，它是一个结构体中包含两个成员。一个是存储数值，一个存放下一个结点的地址。

typedef int SLTDataType;
typedef struct SListNode
{SLTDataType data;struct SListNode* next;
}SListNode;

实际内存存储结构：

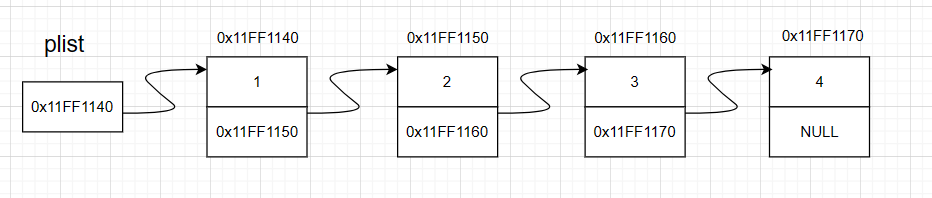
5. 单链表功能实现

5.1 打印单链表

打印链表需要对函数传参指向链表的指针，首先为了保证链表不为空(NULL)，需要对其进行断言。

(1) 代码实现

void PrintSList(SListNode* plist)
{SListNode* cur = plist;while (cur){printf("%d->", cur->data);cur = cur->next;}printf("NULL\n");
}

(2) 复杂度分析

• 时间复杂度：因为需要遍历整个链表，显然时间复杂度为O(N)。
• 空间复杂度：打印链表不需要格外的空间，所以空间复杂度为O(1).

5.2 单链表头插

(1) 创建结点

单链表每次插入都需要插入一个节点，所以我们最好写一个创建节点的函数方便后续调用。

SListNode* SListCreatNode(SLTDataType x)
{SListNode* newnode = (SListNode*)malloc(sizeof(SListNode));if (newnode == NULL){perror("malloc fail:");return;}newnode->data = x;newnode->next = NULL;return newnode;
}

(2) 头插代码实现

单链表的头插与顺序表头插最大的不同就是单链表传参需要二级指针。因为头插数据需要改变一级指针plist的指向，而形参的改变无法影响实参，所以需要二级指针才能改变一级指针plist的指向。

void SListPushFront(SListNode** plist, SLTDataType x)
{assert(plist);SListNode* newnode = SListCreatNode(x);newnode->next = *plist;*plist = newnode;
}

(3) 复杂度分析

• 时间复杂度：不需要额外时间的消耗，时间复杂度为O(1)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

5.3 单链表头删

头删与头插类似，都可能需要改变plist的指向，所以也需要二级指针。并且也需要防止链表为空的情况发生。

(1) 代码实现

void SListPopFront(SListNode** plist)
{assert(plist);assert(*plist);SListNode* cur = (*plist)->next;free(*plist);*plist = cur;
}

(2) 复杂度分析

• 时间复杂度：不需要额外时间的消耗，时间复杂度为O(1)。
• 空间复杂度：不需要格外的空间消耗，空间复杂度为O(1)。

5.4 单链表尾插

当链表为空时，单链表尾插就会变成单链表头插，也需要改变plist的指向。其余情况即可通过循环寻找尾节点。

(1) 代码实现

void SListPushBack(SListNode** plist, SLTDataType x )
{assert(plist);if (*plist== NULL){*plist = SListCreatNode(x);}else{SListNode* ptail = *plist;while (ptail->next){ptail = ptail->next;}ptail->next = SListCreatNode(x);}
}

(2) 复杂度分析

• 时间复杂度：需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

5.5 单链表尾删

与单链表尾插类似，当链表只有一个头结点时需要将plist置为空，所以也需要二级指针。并且也需要防止链表为空的情况发生。

(1) 代码实现

void SListPopBack(SListNode** plist)
{assert(plist);assert(*plist);//防止链表为空if ((*plist)->next == NULL){free(*plist);*plist = NULL;}else{SListNode* ptail = *plist;while (ptail->next->next){ptail = ptail->next;}free(ptail->next);ptail->next = NULL;}	
}

(2) 复杂度分析

• 时间复杂度：需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：不需要格外的空间消耗，空间复杂度为O(1)。

5.6 单链表的查找

如果找到就返回这个节点的地址，否则就返回空指针NULL

(1) 代码实现

SListNode* SListSearch(SListNode* plist, SLTDataType x)
{assert(plist);SListNode* cur = plist;while (cur){if (cur->data == x){return cur;}cur = cur->next;}return NULL;
}

(2) 时间复杂度

• 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：不需要格外的空间消耗，空间复杂度为O(1)。

5.6 单链表的修改

单链表的修改可以与查找配套使用。

(1) 代码实现

void SListModify(SListNode*plist, SListNode* pos, SLTDataType x)
{assert(plist);assert(pos);SListNode* cur = plist;while (cur){if (cur == pos){cur->data = x;break;}cur = cur->next;}
}

(2) 复杂度分析

• 时间复杂度：可能需要遍历整个链表，时间复杂度为O(N)。
• 空间复杂度：不需要格外的空间消耗，空间复杂度为O(1)。

5.7 单链表任意位置的插入

(1) 代码实现

某个位置之前插入，当链表为空或者在头节点插入时使用头插。

void SListInsertF(SListNode** plist, SListNode* pos, SLTDataType x)
{assert(plist);assert(pos);if (*plist == pos || *plist == NULL){SListPushFront(plist, x);//头插}else{SListNode* newnode = SListCreatNode(x);SListNode* prev = *plist;while (prev->next != pos){prev = prev->next;}newnode->next = pos;prev->next = newnode;}
}

某个位置之后插入，当链表为空或者在尾节点插入时使用尾插。

void SListInsertB(SListNode** plist, SListNode* pos, SLTDataType x)
{assert(plist);assert(pos);if (*plist == NULL||pos->next==NULL){SListPushBack(plist, x);//尾插}else{SListNode* tmp = pos->next;SListNode* newnode = SListCreatNode(x);pos->next = newnode;newnode->next = tmp;}
}

(2) 复杂度分析

• 时间复杂度：无论向前插入还是向后插入都可能需要遍历整个链表，所以时间复杂度为O(N)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

5.8 任意位置的删除

任意位置的删除需要提前保存好前一个节点与后一个节点的位置。

(1) 代码实现

void SListErase(SListNode** plist, SListNode* pos)
{assert(plist);assert(*plist);assert(pos);if (*plist == pos){SListPopFront(plist);//头删}SListNode* prev = *plist;while (prev->next!=pos){prev = prev->next;}SListNode* tmp = pos->next;prev->next = tmp;free(pos);pos = NULL;
}

(2) 复杂度分析

• 时间复杂度：可能需要遍历整个链表，所以时间复杂度为O(N)。
• 空间复杂度：固定创造一个节点，空间复杂度为O(1)。

5.9 销毁链表

销毁链表需要依次遍历释放节点。

(1) 代码实现

void SListDestroy(SListNode** plist)
{assert(plist);assert(*plist);SListNode* cur = *plist;while (cur){SListNode* tmp = cur->next;free(cur);cur =tmp;}*plist = NULL;//防止野指针
}

(2) 复杂度分析

• 时间复杂度：需要遍历整个链表，所以时间复杂度为O(N)。
• 空间复杂度：不需要格外的空间消耗，空间复杂度为O(1)。