数据结构——堆的应用堆排序详解

💞💞 前言

hello hello~ ，这里是大耳朵土土垚~💖💖 ，欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹

💥个人主页：大耳朵土土垚的博客
💥 所属专栏：数据结构学习笔记
💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~
有问题可以写在评论区或者私信我哦~

在土土的上篇博客二叉树堆的介绍与实现中，我们发现测试代码是升序；今天我们就来分析堆的重要应用——**堆排序**🎉🎉。

#include"Heap.h"
int main()
{Heap hp;HeapInit(&hp);int a[] = { 65,100,70,32,50,60 };for (int i = 0; i < 6; i++){HeapPush(&hp, a[i]);}while (!HeapEmpty(&hp)){int top = HeapTop(&hp);printf("%d\n", top);HeapPop(&hp);}HeapDestroy(&hp);return 0;
}

在这里插入图片描述
详情可在土土的博客数据结构——lesson7二叉树堆的介绍与实现中查看🥳🥳

一、堆排序（基础版）

既然是堆排序，那我们首先肯定得有一个堆，这里土土就可以偷个懒将上篇博客中实现的堆代码copy一下🥰🥰

堆的实现

#include"Heap.h"
//堆的初始化
void HeapInit(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
// 堆的销毁
void HeapDestroy(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
//交换函数
void Swap(HPDataType* a,HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}//堆向下调整算法
void AdjustDown(HPDataType* a, int n,int parent)
{//找到较小的孩子节点int child = parent * 2 + 1;//向下调整while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}elsebreak;}
}//向上调整
void AdjustUp(HPDataType* a,int child)
{//找到双亲节点int parent = (child - 1) / 2;//向上调整while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);//判断容量if (hp->size == hp->capacity)//容量满了扩容{int newcapacity = hp->capacity == 0 ? 0 : 2 * hp->capacity;HPDataType* new = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (new == NULL){perror("realloc fail");return;}hp->a = new;hp->capacity = newcapacity;}//尾插hp->a[hp->size] = x;hp->size++;//向上调整算法AdjustUp(hp->a,hp->size-1);
}
// 堆的删除，删除堆顶元素
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//向下调整算法AdjustDown(hp->a, hp->size, 0);}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}

当然在使用这些函数时要记得先声明一下，这里我们都放到一个头文件Heap.h中

Heap.h

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int HPDataType;
//构建一个结构体封装堆
typedef struct Heap
{HPDataType* a;//数组顺序表int size;//堆元素个数int capacity;//数组空间
}Heap;
//以下是实现堆的函数
// 堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestroy(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

使用时只需包含该头文件即可
#include"Heap.h"

堆排序

给定一个数组a[ ] = {7,8,3,5,1,9,5,4},我们需要利用上面的堆来将它进行排序

🤩🤩思路：
①我们首先需要将数组中的元素插入堆中（利用HeapPush函数），
💫前面我们已经学习过堆插入函数，它里面利用堆向上调整算法会自动将插入的数据调整为一个堆（我们实现的是小堆）；
②然后我们需要获取堆顶元素（也就是小堆中最小的元素），利用HeapTop函数即可；
③获取最小元素后我们就需要获取次小元素，先利用堆的删除函数（HeapPop函数)，将堆顶元素（也就是小堆中最小的元素）删除；
💞删除函数中堆向下调整算法又会将剩余元素调整为小堆，此时堆顶元素就是删除一个元素后最小的元素；
④将删除后的元素重新拷贝回数组a中；
⑤循环②③两步直到全部排序成功。

代码实现如下：

#include"Heap.h"
void HeapSort(int* a,int size)
{
Heap hp;
HeapInit(&hp);
//将a中元素插入堆中
for (int i = 0; i < size; i++)
{
HeapPush(&hp, a[i]);
}
//获取堆顶（最小）元素并删除
int i = 0;
while (i < size)
{
a[i++] = HeapTop(&hp);
HeapPop(&hp);
}
HeapDestroy(&hp);
}
int main()
{
int a[] = { 7,8,3,5,1,9,5,4 };
int size = sizeof(a) / sizeof(int);
HeapSort(a,size);
return 0;
}

🥳🥳结果如下：
排序前：
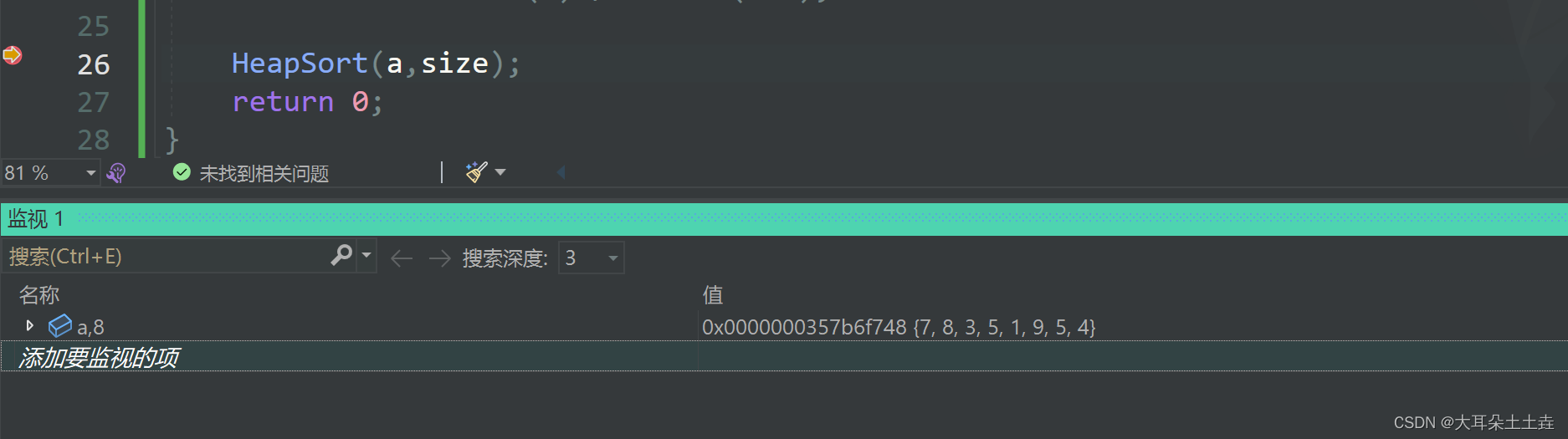
在这里插入图片描述
排序后：

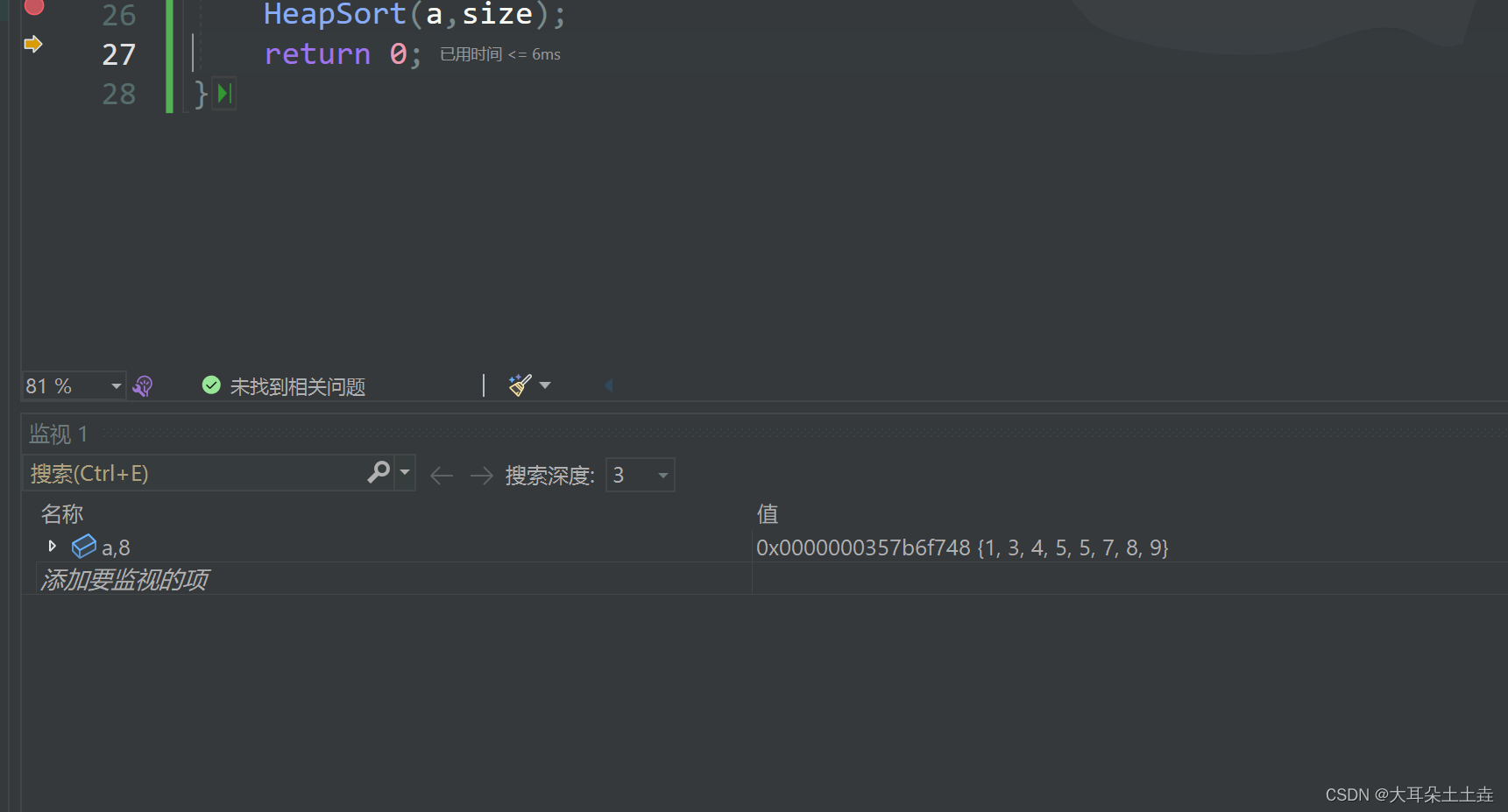
💥💥上述堆排序的实现尽管能够实现排序，但是…我们发现如果没有提前实现堆或者准备好堆的代码，我们是没办法实现的，而且我们需要来回拷贝数据，空间复杂度较大。
🥰🥰这里就需要介绍下面简便版堆排序啦~

二、堆排序（简便版）

在土土的数据结构学习笔记数据结构——lesson7二叉树堆的介绍与实现中，详细介绍了堆向上调整算法与堆向下调整算法，接下来我们就可以利用这两个函数来实现堆以及堆的排序🥳🥳

（1）利用堆向上调整算法实现堆

//向上调整算法
void AdjustUp(HPDataType* a,int child)
{//找到双亲节点int parent = (child - 1) / 2;//向上调整while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}

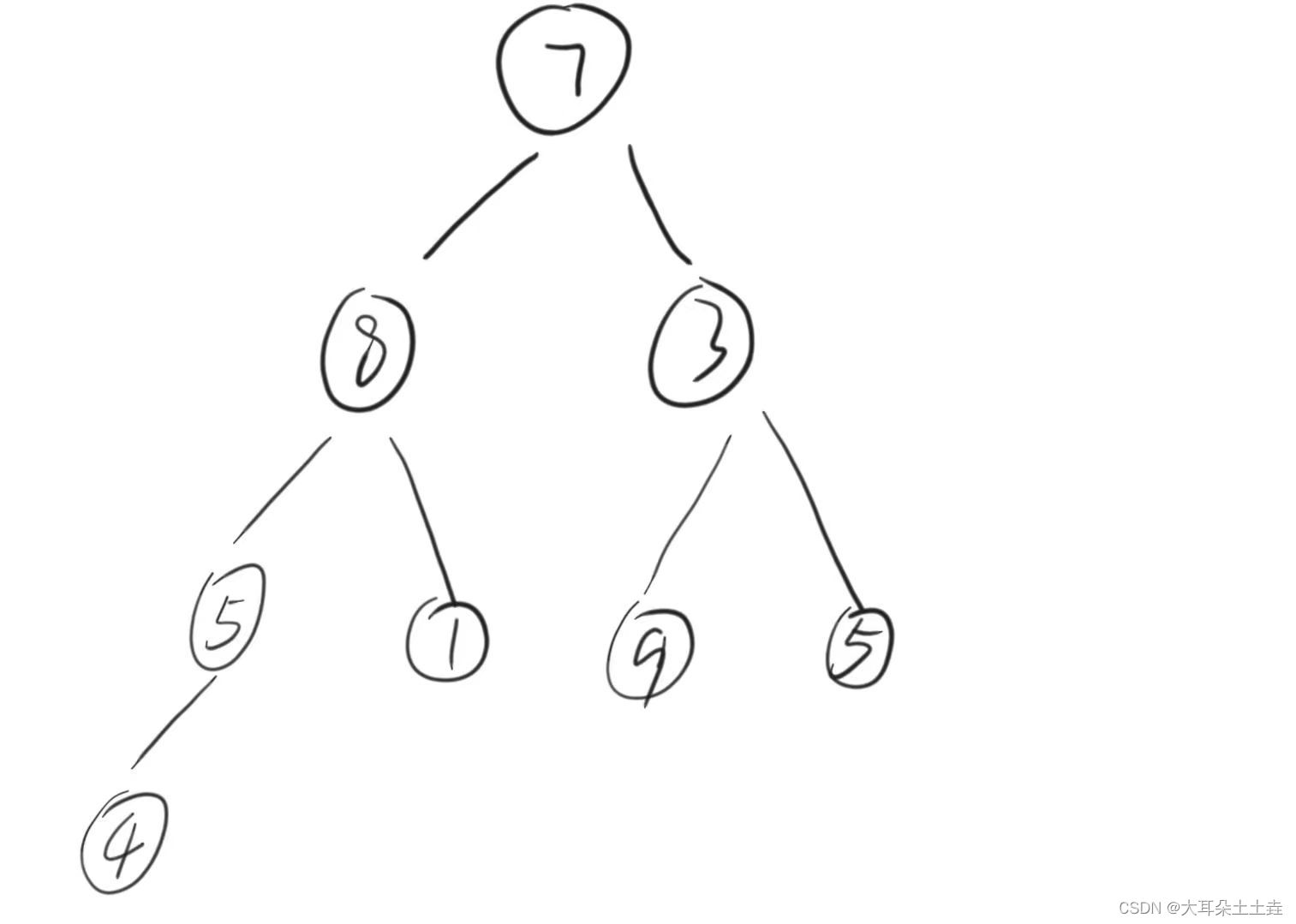
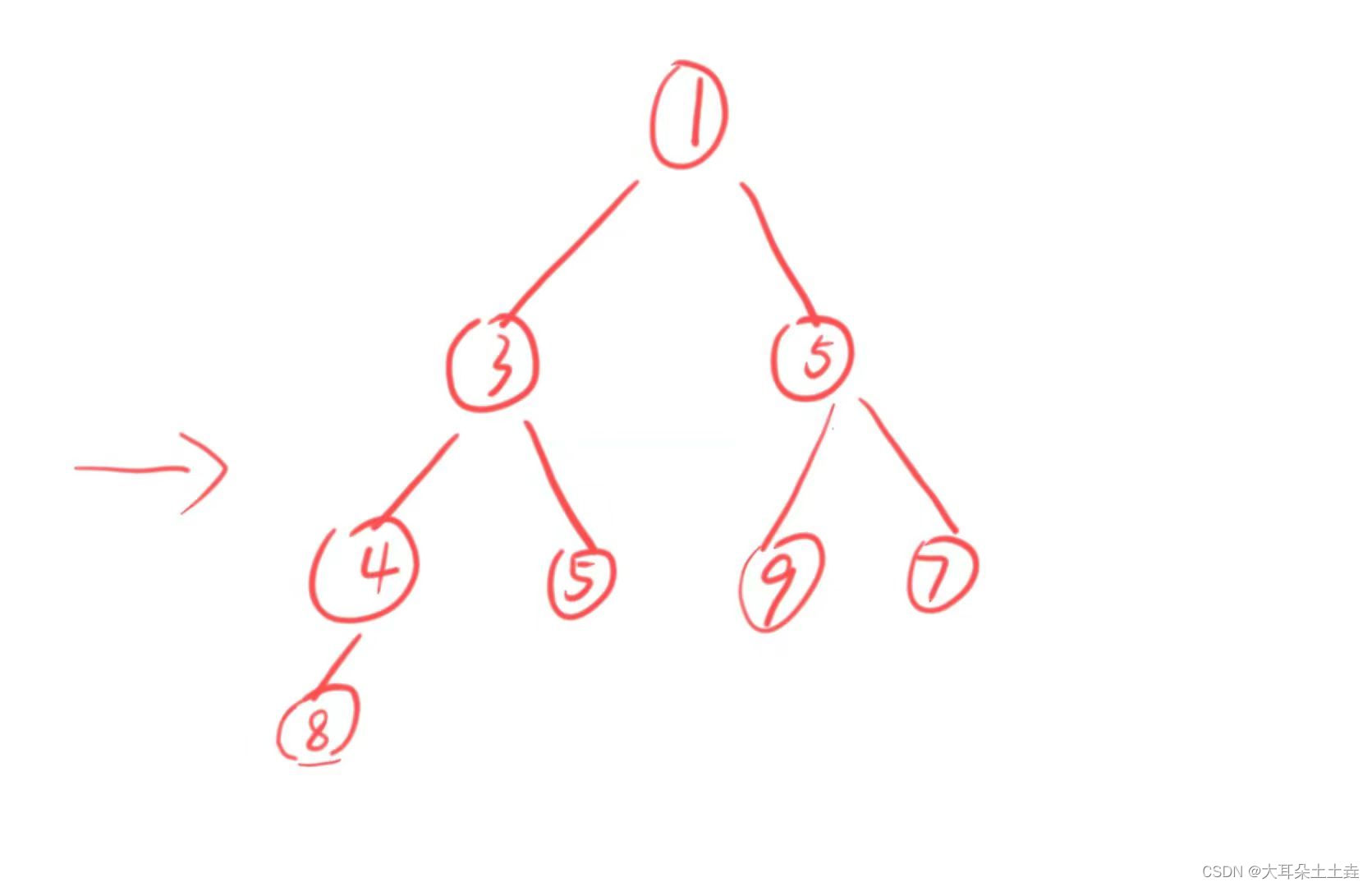
数组a[ ] = {7,8,3,5,1,9,5,4}，我们可以看成一个二叉树：

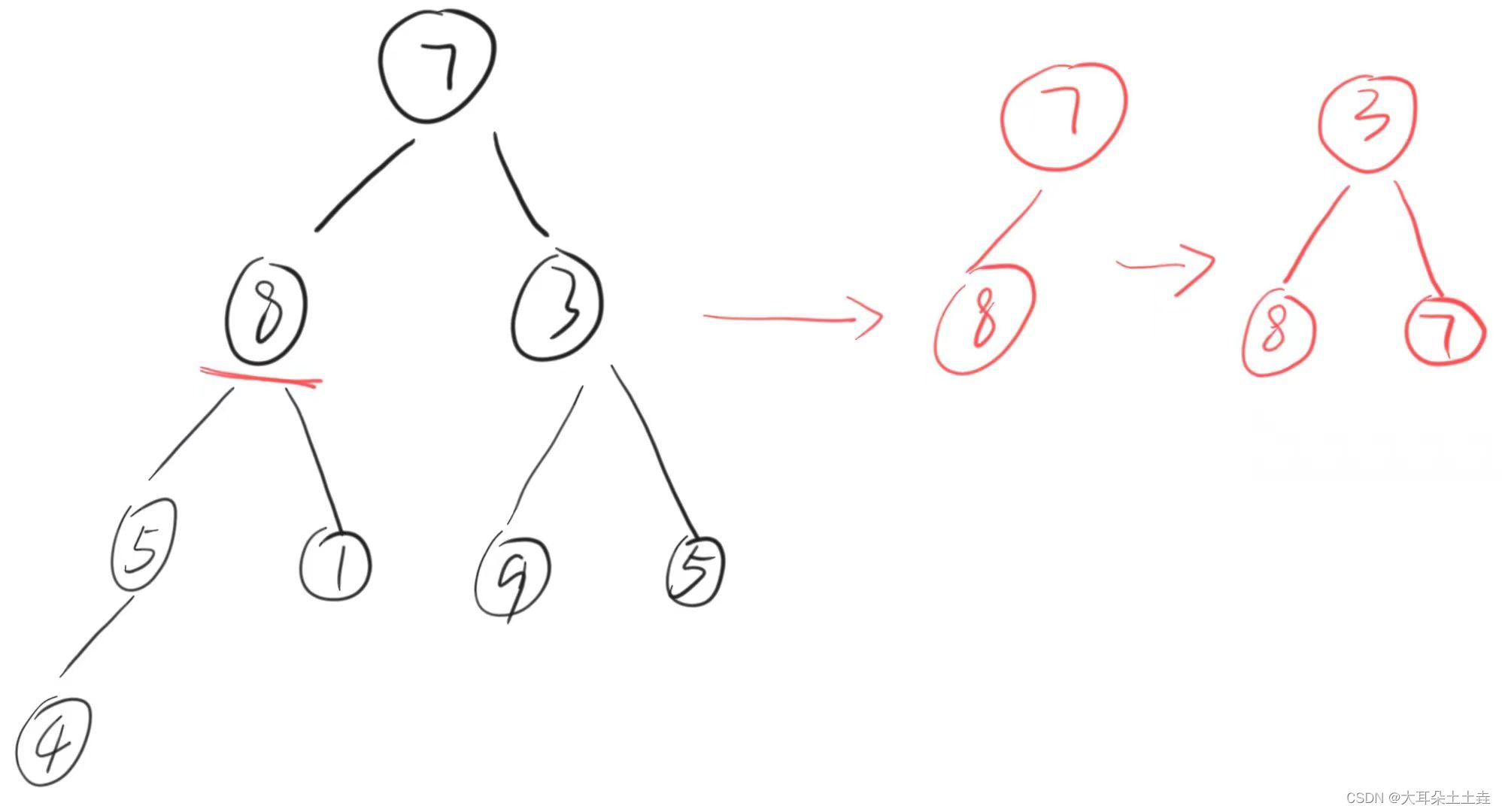
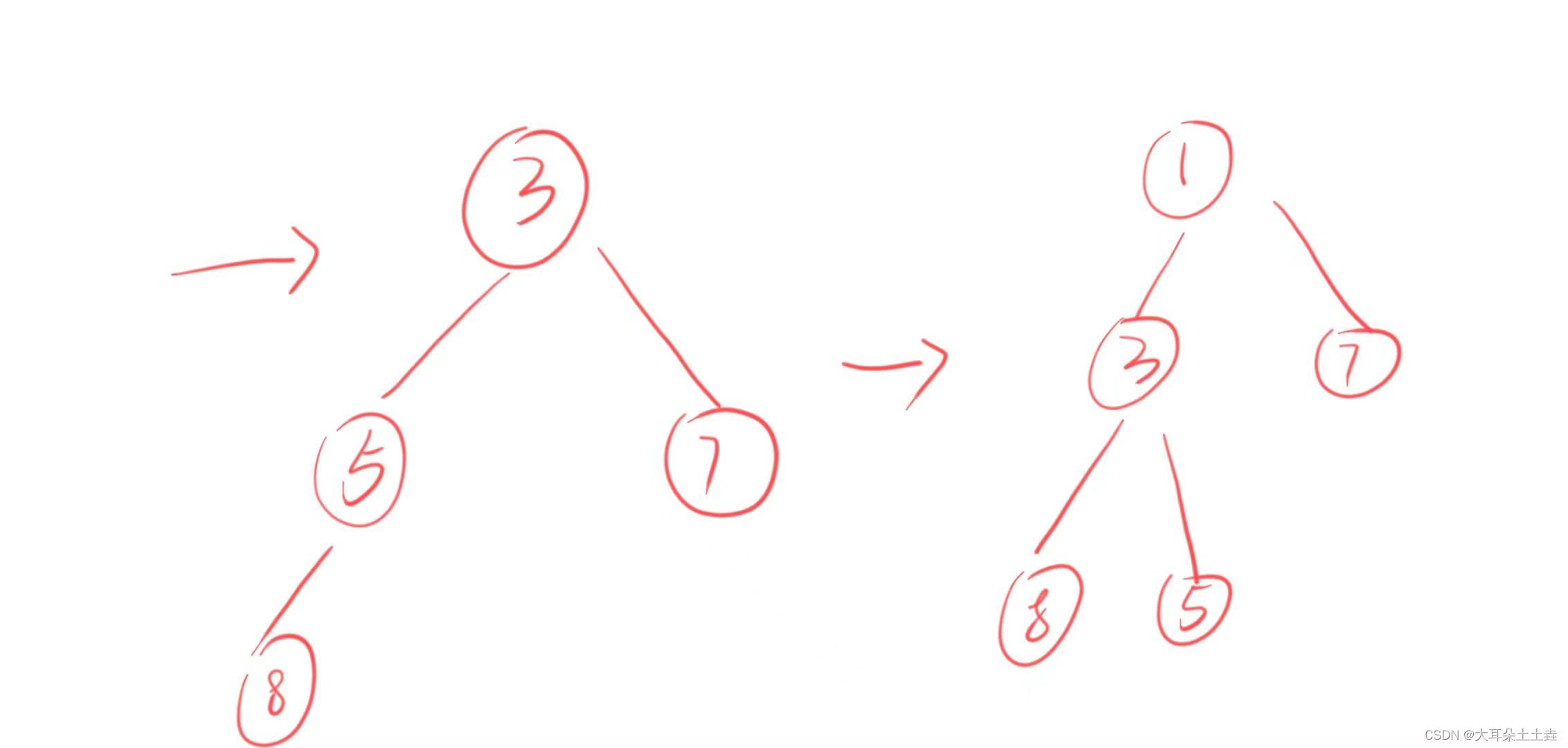
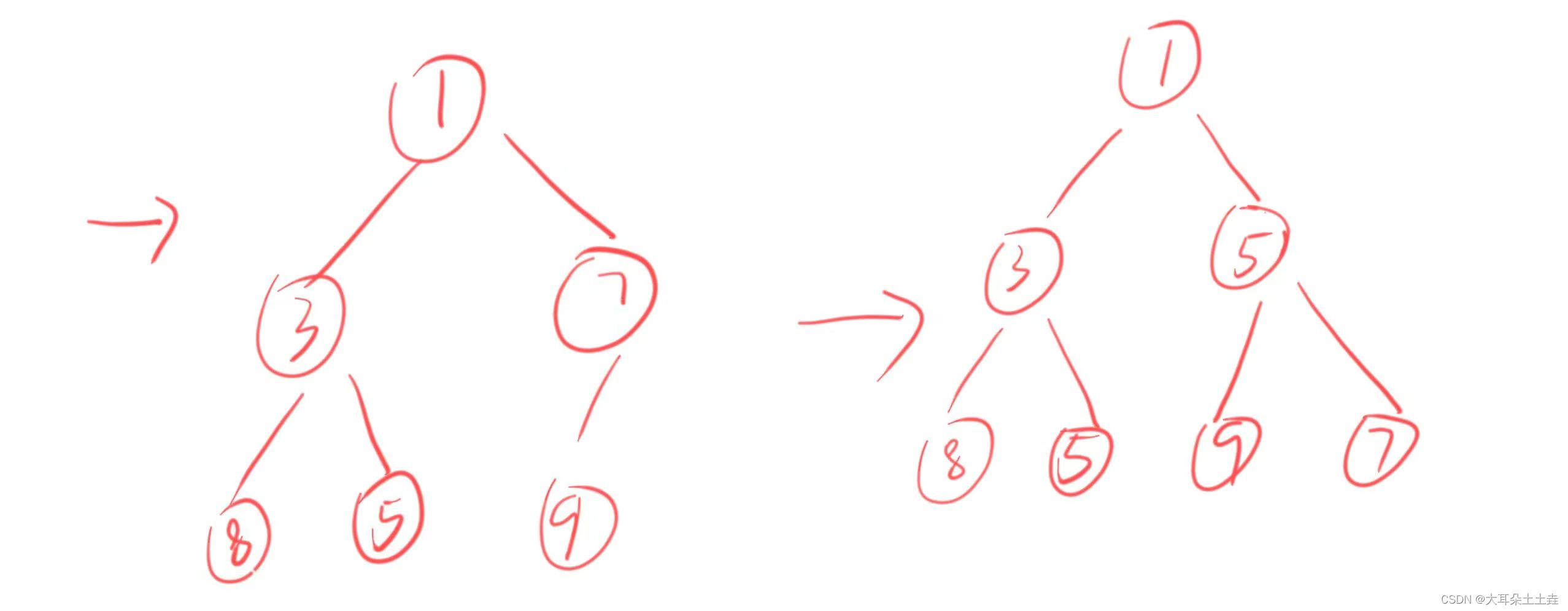
只需要从第二个数8开始每次读取一个数据都向上调整为堆，那么读完整个数组就可以得到一个堆啦~🥰🥰

//从第二个数据开始向上调整建堆
for (int i = 1; i < size; i++)
{AdjustUp(a, i);
}

🤩🤩之前基础版排序是又开辟了一个空间来存放a中的数据，排成堆后又每次选取最小的元素拷贝回a中，不仅麻烦而且会增加空间的使用；
所以简便版排序便直接将a看成一个二叉树利用向上调整算法直接成堆，不需要开辟额外的空间。

（2）利用堆向下调整算法排序

那我们应该怎么将堆中的元素排序呢？
🥳🥳这就要利用堆向下调整算法了

思路🥳🥳

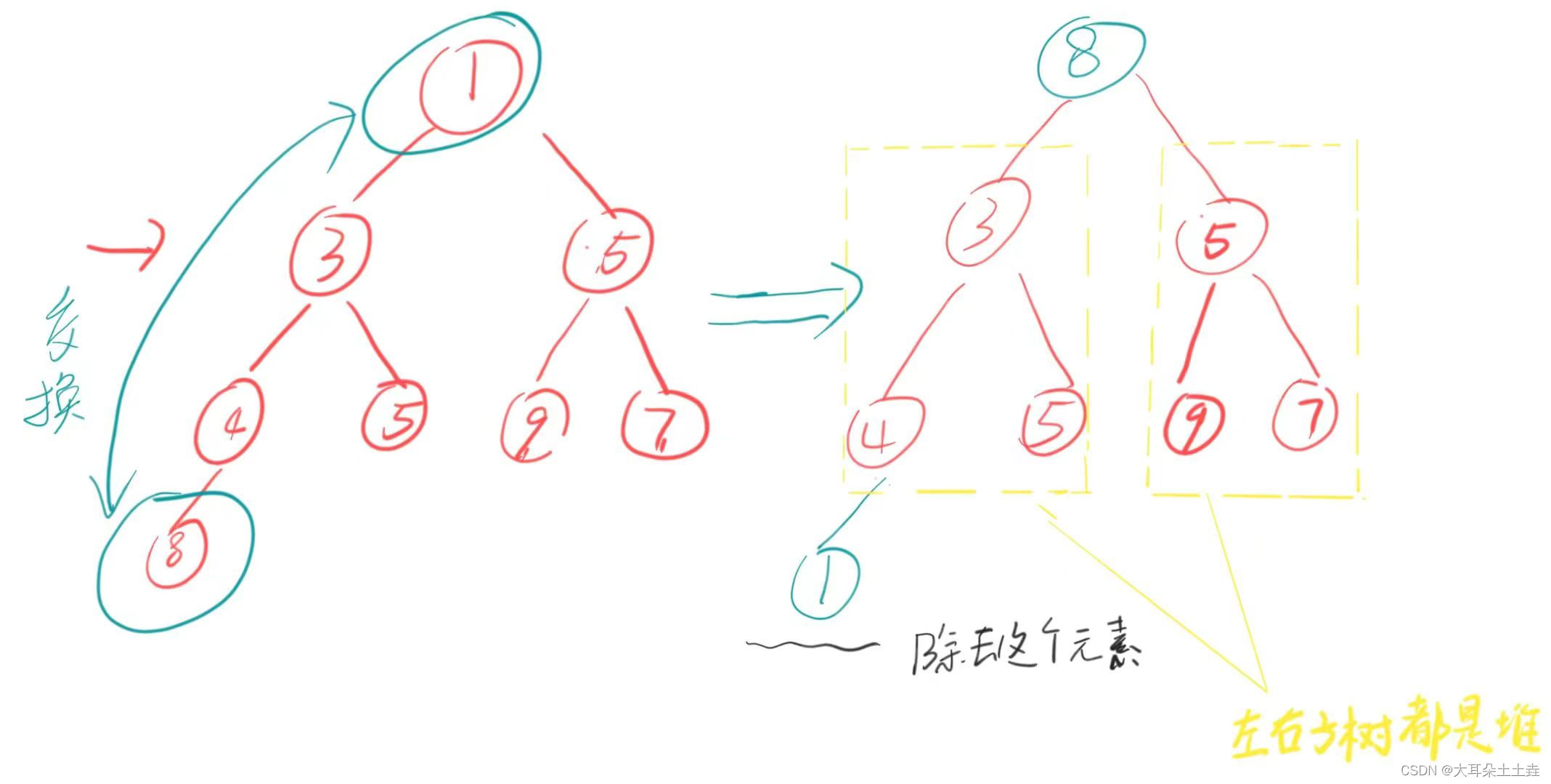
①交换首尾元素，将堆中最小的元素（首元素）换到尾部；
②将交换后的尾部元素忽略，剩余元素利用堆向下调整算法（除头外左右子树都是堆）调整为堆；

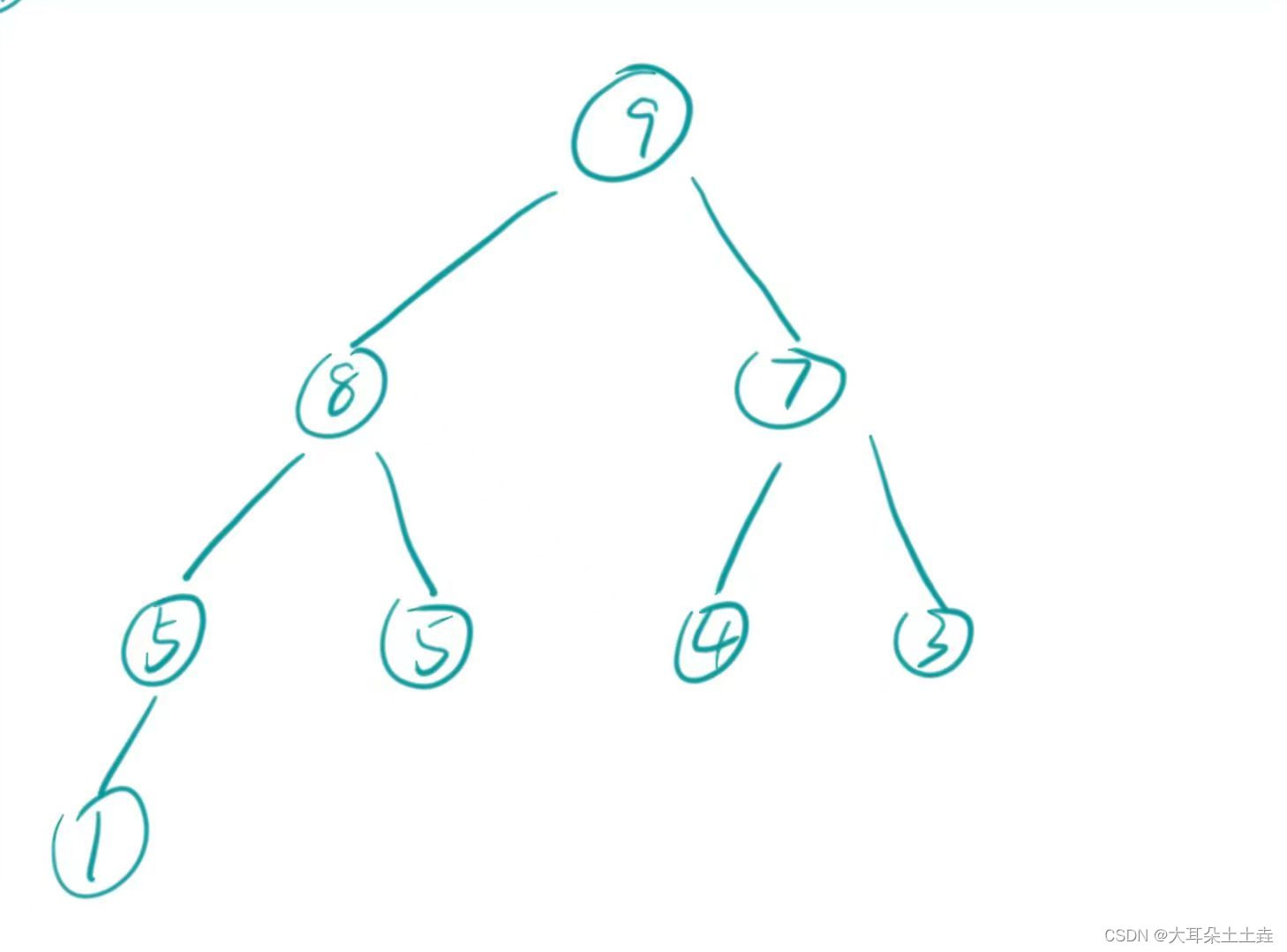
③重复②直到全部排完，得到降序数组：

代码如下：

//排序
int end = size-1;//堆底元素下标
while (end)
{Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;
}

🤩🤩Swap函数在这里：

//交换函数
void Swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}

（3）完整实现🥳🥳

void HeapSort(int* a,int size)
{//从第二个数据开始向上调整建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}//排序int end = size-1;//堆底元素下标while (end){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}}
int main()
{int a[] = { 7,8,3,5,1,9,5,4 };HeapSort(a, 8);return 0;
}

结果如下：
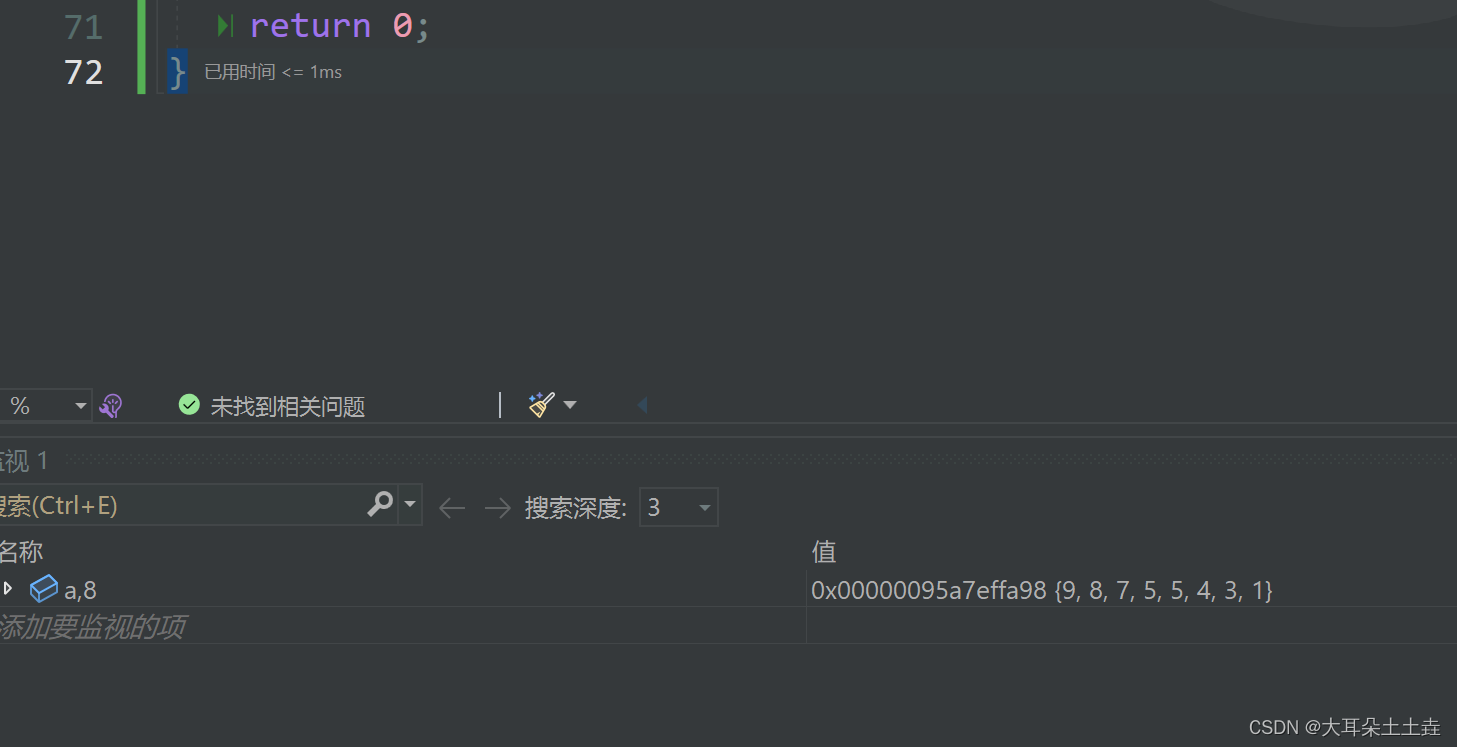
在这里插入图片描述