week29 Beyond Dropout

摘要

本文主要讨论Dropout方法及其改进。本文简要介绍了泛化理论。其次本文展示了题为Beyond Dropout: Feature Map Distortion to Regularize Deep Neural Networks的论文主要内容。该文研究了与深度神经网络中间层相关的经验Rademacher复杂度，在此基础上提出了一种特征失真的方法。实验表明，与传统的dropout方法相比，该方法能够更加有效的训练神经网络。

Abstract

This article mainly talks about the Dropout method and its improvements. This article briefly introduces the theory of generalization. Secondly, this paper presents the main content of the paper titled Beyond Dropout: Feature Map Distortion to Regularize Deep Neural Networks. This paper studies the empirical Rademacher complexity associated with the middle layer of deep neural networks and proposes a feature distortion method on this basis. Experiments show that compared with the traditional dropout method, the proposed method can train the neural network more effectively.

一、泛化理论

泛化理论关注预期风险与经验风险之间的关系。考虑 $L-layer$ 神经网络 $f^L\in F$，以及从真值分布 $Q\in X\times Y$ 采样的标记数据集 $\mathcal{D}=\{(x_i,y_i){\}}_{i=1}^N$，其中$ x_i ∈ X, y_i ∈ Y$。权重矩阵为 $K^l\in {\mathbb{R}}^{d^l\times d^{l-1}}$，其中 $d^l$ 为第 l 层特征图的维度，第 l 层激活函数 $\phi$ 前后对应的输出特征为 $o^l\in {\mathbb{R}}^{d^l},f^l\in {\mathbb{R}}^{d^l}$ 。忽略偏差，有 $f^{l+1}(x_i)=\phi (o^{l+1}(x_i))=\phi (K^{l+1}{f}^l(x_i))$。为了简单起见，进一步将使用$K^{:l}$表示 { K 1 ， ⋅ ⋅ ⋅ ⋅ ， K l } \{K^1，····，K^l\} {K1，⋅⋅⋅⋅，Kl}。

以图像分类任务为例，总体上的预期风险 $R(f^L)$ 和训练集上的经验风险 $\hat{R}(f^L)$可表示为：
$$R(f^L)={\mathbb{E}}_{(x,y)\sim Q}[l(f^l(x,K^{:L}),y)]\text{\hspace{1em}(1)}$$

$$\hat{R}(f^L)=\frac{1}{N}\sum _{(x_i,y_i)\in \mathcal{D}}l(f^L(x_i,K^{:L}),y_i)\text{\hspace{1em}(2)}$$

其中$l(\cdot )$​表示0-1损失。

ERC的正式定义如下： 对于给定的由分布Q生成的具有N个实例$\mathcal{D}=\{(x_i,y_i)\}$的训练数据集，网络函数类$f^L$的经验Rademacher复杂度定义为：
$$\sim R_D(f^L)=\frac{1}{N}{\mathbb{E}}_{\sigma }|su{p}_{k,K^{:L}}\sum _{i=1}^N{\sigma }_i{f}^L(x)|$$
其中 Rademacher 变量 $\sigma ={\sigma }_1,\cdot \cdot \cdot ,{\sigma }_N$, ${\sigma }_i$ 是 {-1,+1} 中的独立均匀随机变量，$f^L(x_i,K^{:L})[k]$ 是$f^L(x_i，K^{:L})$​ 中的第 k 个元素。

使用经验 Rademacher 复杂度和 MaDiarmid 不等式，预期风险 R(fL) 的上限可以通过定理 1 得出

定理1：给定固定的 $\rho >0$，对于任何 $\delta >0$，对于所有 $f^L\in F$，概率至少为 $1-\delta$
$$R(f^L)\le \hat{R}(f^L)+\frac{2(d^L{)}^2}{\rho }{\hat{R}}_D(f^L)+(1+\frac{2(d^L{)}^2}{\rho }\sqrt{\frac{\ln \frac{1}{\theta }}{2N}})\text{\hspace{1em}(4)}$$
其中 $d^L$​ 表示网络的输出维度。

根据定理 1，预期风险和经验风险之间的差距可以借助特定神经网络和数据集上的经验 Rademacher 复杂度 R∼ D(f) 来限制。直接计算 ERC 是很困难的，因此 ERC 的上限或近似值通常在训练阶段使用，以获得具有更好泛化能力的模型。通过减少与 ERC 相关的正则化项，获得了具有更好泛化能力的模型。

二、文献阅读

1. 题目

题目：Beyond Dropout: Feature Map Distortion to Regularize Deep Neural Networks

作者：Yehui Tang, Yunhe Wang, Yixing Xu, Boxin Shi, Chao Xu, Chunjing Xu, Chang Xu

链接：https://arxiv.org/abs/2002.11022

发表：AAAI2020

2. abstract

基于 dropout 的方法在训练阶段禁用输出特征图中的某些元素，以减少神经元的共同适应。尽管这些方法可以增强所得模型的泛化能力，但传统的二元 dropout 并不是最佳解决方案。因此，该文研究了与深度神经网络中间层相关的经验Rademacher复杂度，并提出了一种特征失真方法（Disout）来解决上述问题。

Dropout based methods disable some elements in the output feature maps during the training phase for reducing the co-adaptation of neurons. Although the generalization ability of the resulting models can be enhanced by these approaches, the conventional binary dropout is not the optimal solution. Therefore, this paper investigate the empirical Rademacher complexity related to intermediate layers of deep neural networks and propose a feature distortion method (Disout) for addressing the aforementioned problem.

3. 网络架构

该文的目标不是固定扰动值，而是通过降低网络的ERC来学习特征图的失真。一般来说，对输入数据$x_i$的第l层的输出特征$f^l(x_i)$进行的干扰操作可以表示为
$${\hat{f}}^l(x_i)=f^l(x_i)-m_i^l\circ {ϵ}_i^l\text{\hspace{1em}(6)}$$
其中${ϵ}_i^l\in {\mathbb{R}}^{d^l}$是作用于特征图$f^l(x_i)$的失真。相较于原始的dropout方法，上式自动学习是根据ERC推导的失真形式。由于ERC在最后一层上计算的，故在神经网络上直接使用ERC是困难的。在训练阶段很难追踪神经网络的中间特征。故需要考虑任意层的输出特征来重新表征${\tilde{R}}_D(f^L)$，从而有以下定理

$\mathbf{Theorem}2$ 令${\mathcal{K}}^l[k,:]$表示参数矩阵${\mathcal{K}}^l$的k行，而$||\cdot |{|}_p$是向量的p范数。假定$||K^l[k,:]|{|}_p\le B^l$,则输出的ERC可以由中间特征的ERC限制:
$$\begin{gathered} {\tilde{R}}_D(f^L)\le 2{\tilde{R}}_D(o^L)\le 2B^L{\tilde{R}}_D(f^{L-1})\le \dots \\ \le 2^{L-t}{\tilde{R}}_D(f^t)\prod _{l=t+1}^L{B}^l\le 2^{L-t+1}{\tilde{R}}_D(o^t)\prod _{l=t+1}^L{B}^l\text{\hspace{1em}(7)} \end{gathered}$$
其中$o^l,f^l$分别是激活函数之前和之后的特征映射。

上述理论展示了网络${\tilde{R}}_D(f^L)$的ERC由第t层的输出特征${\tilde{R}}_D(f^t)$或${\tilde{R}}_D(o^t)$的ERC确定上界。故降低${\tilde{R}}_D(f^t)$或${\tilde{R}}_D(o^t)$可以降低${\tilde{R}}_D(f^L)$。$f^t$是网络任意中间层t的特征图，且失真也能应用于中间特征。故${\tilde{R}}_D(f^t)$或${\tilde{R}}_D(o^t)$可以作为失真操作的根据。

3.1 特征图失真

本节说明通过在第l层的特征图上应用失真来降低$f^l(x_i)$的ERC。通过该操作，后续层中所有ERC都会受到影响，满足$l<t\le L$的${\tilde{R}}_D(o^t)$可以影响第l层的失真${ϵ}_i$。距离输出层越近的层，整个网络的ERC上限越紧，且能更有效地减少${\tilde{R}}_D(f^L)$。但若$t\le l$，${\tilde{R}}_D(o^t)$和$ϵ$之间的关系更加复杂，且很难使用${\tilde{R}}_D(o^t)$影响${ϵ}_l$。故使用第l+1层${\tilde{R}}_D(o^{l+})$的ERC来引导第l层。即通过优化${ϵ}_l$来降低${\tilde{R}}_D(o^{l+1})$，从而有下式
$$g^l(x)=\sum _{i=1}^N{\sigma }_i{\hat{f}}^l(x_i)\text{\hspace{1em}(8)}$$
令$g^l(x)\in {\mathbb{R}}^{d^l}$与特征图$f^l(x_i)$维度相同，则${\tilde{R}}_D(o^{l+1})$如下式
$${\tilde{R}}_D(o^{l+1})=\frac{1}{N}{\mathbb{E}}_{ϵ}{\text{sup}}_{k,{\mathcal{K}}^{:l+1}}|<{\mathcal{K}}^{l+1}[k,:{]}^T,g^l(x)>|\text{\hspace{1em}(9)}$$
其中${\mathcal{K}}^{l+1}[k,:]\in {\mathbb{R}}^{1\times d^l}$表示参数矩阵${\mathcal{K}}^{l+1}$第k行， K : l + 1 = { K 1 , K 2 , ⋯ , K l + 1 } \mathcal K^{:l+1}=\{\mathcal K^1, \mathcal K^2,\cdots, \mathcal K^{l+1}\} K:l+1={K1,K2,⋯,Kl+1}。理想情况下，${ϵ}^l$将减少下一层${\tilde{R}}_D(o^{l+1})$ERC的同时保持表示能力。

在训练阶段，考虑一个具有 $\overline{N}$ 样本的小批量$\overline{x}=x_1,x_2,\cdot \cdot \cdot x_{\overline{N}}$，第 l 层的掩模和畸变为 $m^l=m_1^l,m_2^l,\dots ,m_{\overline{N}}^l$ 和 ${\epsilon }^l={\epsilon }_1^l,{\epsilon }_2^l,\dots ,{\epsilon }_{\overline{N}}^l$。以分类问题为例，通过最小化交叉熵损失来更新网络的权重。基于当前更新的权值${\mathcal{K}}^l$和Rademacher变量$\overline{\sigma }={\sigma }_1,{\sigma }_2,\dots ,{\sigma }_{\overline{N}}$，通过求解优化问题得到优化后的扰动${\widehat{ϵ}}^l$：
$${\widehat{ϵ}}^l=\arg \underset{{ϵ}^l}{\min }\mathcal{T}(\overline{x},{ϵ}^l),l=1,2,\dots ,L\text{\hspace{1em}(10)}$$
其中
$$\mathcal{T}(\overline{x},{ϵ}^l)=\frac{1}{N}[su{p}_k|<{\mathcal{K}}^{l+1}[k,:{]}^T,g^l>|+\frac{\lambda }{2}\sum _{i=1}^{\overline{N}}||{ϵ}_i^l|{|}_2^2]\text{\hspace{1em}(11)}$$
其中$||\cdot |{|}_2$表示l2范数，$\lambda$是平衡目标函数和失真强度的超参数

3.2 失真优化

4. 文献解读

4.1 Introduction

由于深度网络通常会过度参数化以在训练集上获得更高的性能，因此一个重要的问题是避免过度拟合。经验风险应该接近预期风险。为此，首先提出了传统的二元dropout方法，该方法通过在训练阶段随机丢弃部分神经元来减少神经元的共同适应。该操作可以被视为模型集成技术或数据增强方法，它显着增强了测试集上所得网络的性能。现有的 dropout 变体为最小化预期风险和经验风险之间的差距做出了巨大的努力，但它们都遵循禁用神经网络中任意层的部分输出的一般思想。

本文提出了一种根据特征图上的失真增强深度神经网络泛化能力的新方法。给定深度神经网络的泛化误差界是根据其中间层的Rademacher复杂度建立的。在特征图上引入失真以降低相关Rademacher复杂度，这有利于提高神经网络的泛化能力。基准图像数据集的实验结果表明，使用所提出的特征失真方法训练的深度网络比使用最先进的方法生成的深度网络表现更好。

4.2 创新点

1. 对dropout方法及其改进方法进行了研究
2. 使用Rademacher复杂度作为依据设计新方法，从而提高了神经网络的泛化能力

4.3 实验过程

在本节中，在几个基准数据集上进行实验，以验证所提出的特征图失真方法的有效性。该方法在 FC 层和卷积层上实现，并分别使用传统 CNN 和现代 CNN（例如 ResNet）进行验证。为了为不同层设置统一的超参数γ，将γ乘以每一层中特征图的标准差，并交替更新失真和权重以提高效率。失真概率（dropout 和 dropblock 的丢弃概率）从 0 线性增加到指定的失真概率 p（Ghiasi、Lin 和 Le 2018^[2]）。

4.3.1 全连接层实验

数据集：在 CIFAR-10 和 CIFAR100 数据集上的传统 CNN 上进行了实验。将所提出的方法与多种最先进的 dropout 变体进行比较。CIFAR-10和CIFAR-100数据集均包含60000张尺寸为32×32的自然图像。其中50000张图像用于训练，10000张图像用于测试。图像分别分为10类和100类。 20%的训练数据被视为验证集。数据增强方法不用于公平比较。

实施细节：传统的 CNN 具有三个卷积层，分别具有 96、128 和 256 个滤波器。每层由步幅为 1 的 5 × 5 卷积运算组成，后跟步幅为 2 的 3 × 3 最大池运算。然后将特征发送到两个全连接层，每个层有 2048 个隐藏单元。调整每个 FC 层上的失真方法。畸变概率 p 从 {0,4, 0.5, 0.6} 中选择，步长 γ 设置为 5。模型训练 500 个 epoch，批量大小为 128。学习率初始化为 0.01，衰减系数为10 在 200、300 和 400 epoch。使用不同的随机种子运行方法 5 次，并汇总平均准确度和标准差。

比较方法：使用一般的没有额外正则化操作的CNN模型作为基础模型。此外，将该文中的方法与广泛使用的dropout方法和几个最先进的变体进行比较，包括Vardrop、Sparse Vardrop、RDdrop

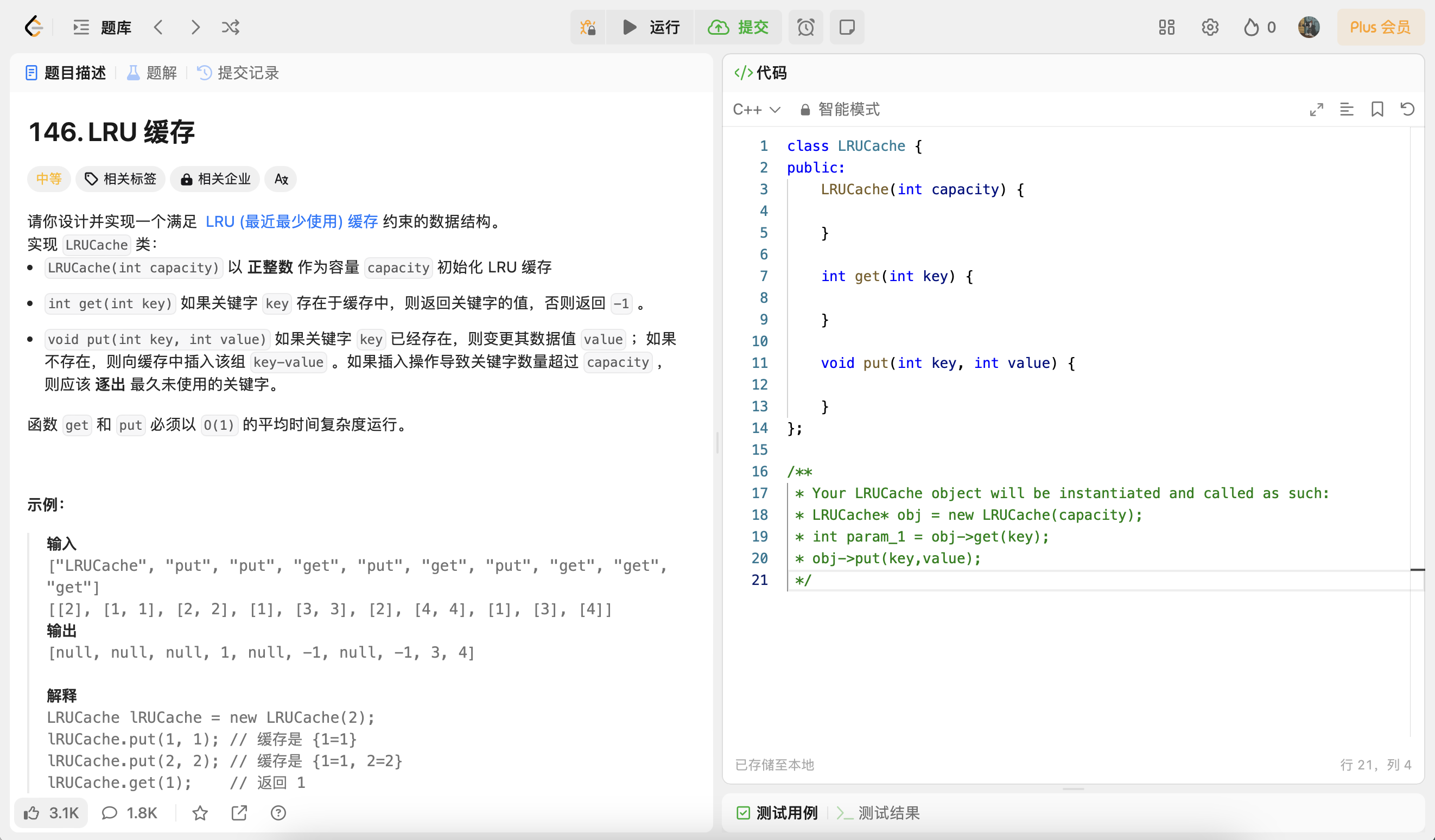
结果：下表总结了 CIFAR-10 和 CIFAR-100 上的测试精度。在该方法的帮助下训练的 CNN 达到了 85.24% 的准确率，这使得最先进的 RDdrop 方法在 CIFAR-10 和 CIFAR-100 数据集上的性能分别提高了 2.13% 和 1.58%。

4.3.2 卷积网络上的实验

将所提出的方法应用于卷积层，并在 CIFAR-10 和 CIFAR-100 数据集上进行了多次实验

实现细节：广泛使用的 ResNet-56包含三组块，被用作基线模型。 使用DropBlock 方法作为本文方法的比较对象。二者都是在最后一组块大小=6 中的每个卷积层之后实现的，并且失真概率（DropBlock 的丢弃概率）p $\in$​ {0.01, 0.02, …, 0.1}。根据经验，步长γ设置为30。训练期间进行标准数据增强，包括随机裁剪、水平翻转和旋转（±15度以内）。网络训练了 200 个 epoch，批量大小设置为 128，权重衰减设置为 5e-4。初始学习率设置为 0.1，并在 60、120 和 160 epoch 时衰减 5 倍。使用不同的随机种子将所有方法重复 5 次，并报告带有标准差的平均准确度。

结果：CIFAR-10和CIFAR-100数据集上的结果如下表。所提出的方法优于DropBlock方法，性能分别提高了0.32%和0.63%。

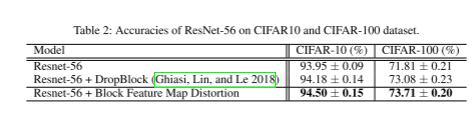
训练曲线： CIFAR-100数据集上的训练曲线如下图所示。实线和虚线分别表示测试阶段和训练阶段，红线和蓝线表示提出的特征图失真方法和基线模型。当训练收敛时，基线ResNet-56陷入过拟合问题，取得了较高的训练精度但较低的测试精度，而所提出的特征图失真方法克服了这一问题并实现了较高的测试精度，这表明模型泛化能力的提高。

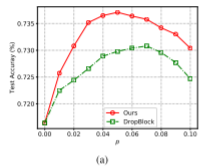
特征图失真（红色）与Dropblock（绿色）在不同失真概率p下在CIFAR-100数据机上的测试精度如下图所示。增大p可以增强正则化效率，将p设置在适当的范围内可提高测试精度。

此外，该文还在ImageNet上进行了实验，同样取得了较好的效果。

4.4 结论

基于 Dropout 的方法已成功运用增强深度神经网络的泛化能力。然而，消除神经网络中的一些单元可以被视为一种启发式方法，用于最小化所得网络的预期风险和经验风险之间的差距，这在实践中并不是最佳方法。该文建议通过利用 Rademacher 复杂度将扭曲嵌入到给定深度神经网络的特征图上。大量的实验结果表明，特征失真技术可以轻松嵌入到主流深度网络中，以在基准数据集上获得比传统方法更好的性能。

小结

本周主要学习了dropout相关技术。首先，简要学习了泛化理论。其次，本周阅读了一篇改进dropout技术的论文，该文引入特征图失真以降低相关Rademacher复杂度，这有利于提高神经网络的泛化能力。

下周将继续阅读环境领域的人工智能相关论文，并继续学习接下来可能使用的数学工具。

参考文献

[1] Yehui Tang, Yunhe Wang, Yixing Xu, Boxin Shi, Chao Xu, Chunjing Xu, Chang Xu: Beyond Dropout: Feature Map Distortion to Regularize Deep Neural Networks.[J].arXiv:2002.11022

[2] Ghiasi, G.; Lin, T.-Y.; and Le, Q. V. 2018. Dropblock: A regularization method for convolutional networks. In Advances in Neural Information Processing Systems, 10727–10737.