LC打怪录数组array

数组（Array）

definition: 一种线性表数据结构。它使用一组连续的内存空间，来存储一组具有相同类型的数据。

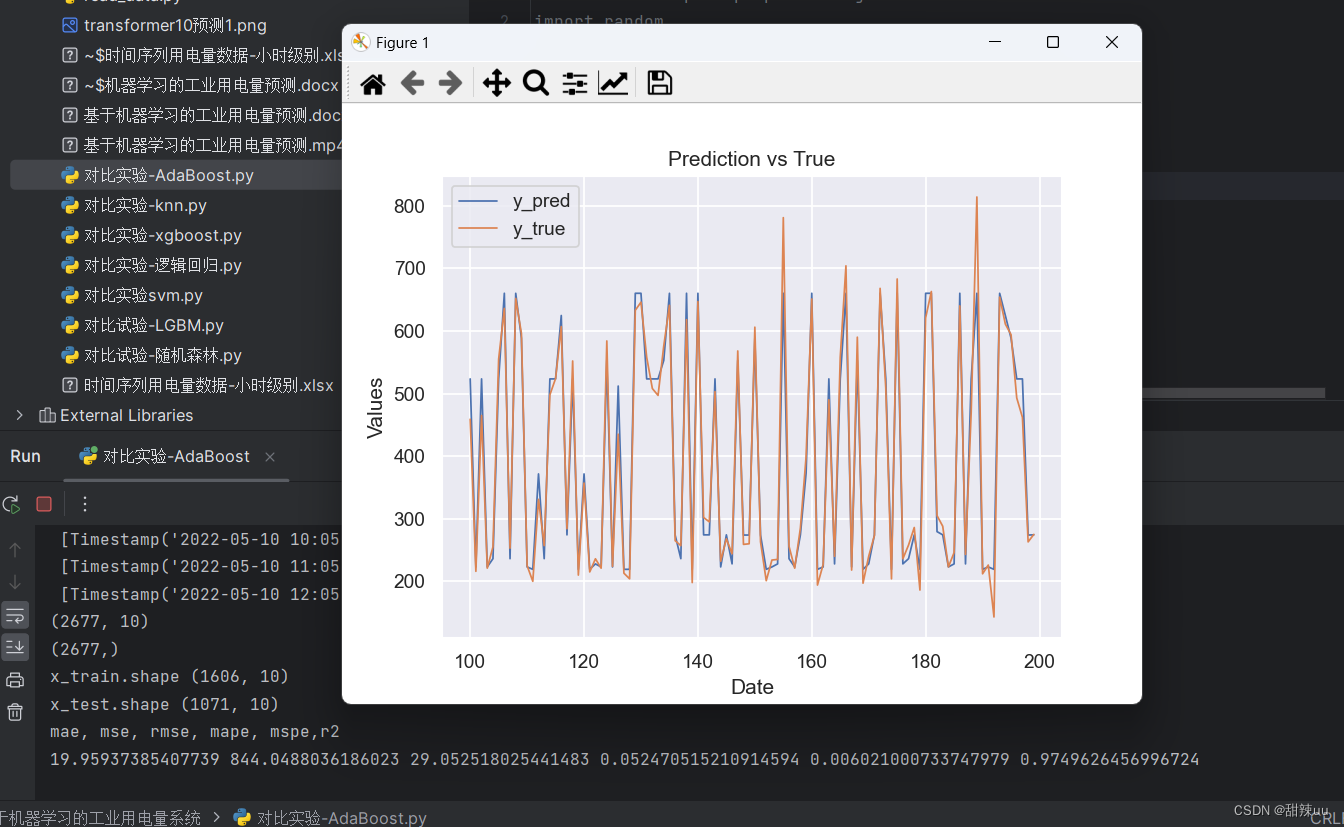
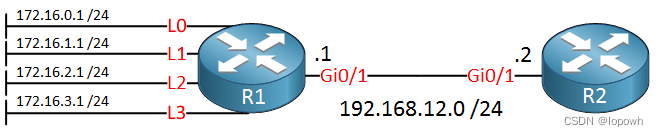
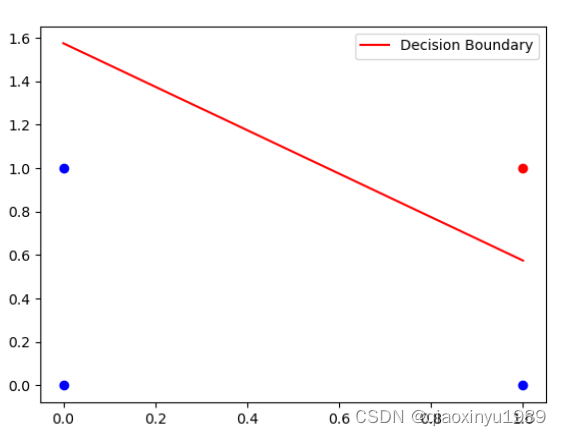
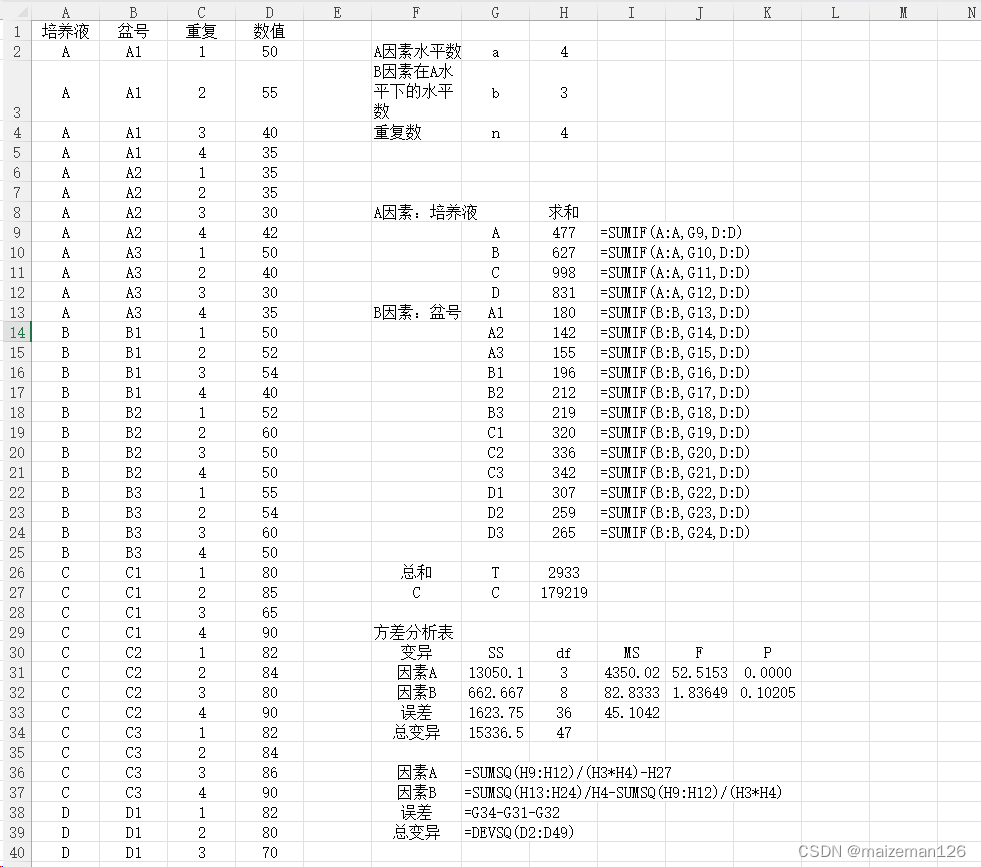
如上图所示，假设数据元素的个数为 nnn，则数组中的每一个数据元素都有自己的下标索引，下标索引从 000 开始，到 n−1n - 1n−1 结束。数组中的每一个「下标索引」，都有一个与之相对应的「数据元素」。

从上图还可以看出，数组在计算机中的表示，就是一片连续的存储单元。数组中的每一个数据元素都占有一定的存储单元，每个存储单元都有自己的内存地址，并且元素之间是紧密排列的。

线性表：线性表就是所有数据元素排成像一条线一样的结构，线性表上的数据元素都是相同类型，且每个数据元素最多只有前、后两个方向。数组就是一种线性表结构，此外，栈、队列、链表都是线性表结构。
连续的内存空间：线性表有两种存储结构：「顺序存储结构」和「链式存储结构」。其中，「顺序存储结构」是指占用的内存空间是连续的，相邻数据元素之间，物理内存上的存储位置也相邻。数组也是采用了顺序存储结构，并且存储的数据都是相同类型的。

原生 Python 中其实没有数组的概念，而是使用了类似 Java 中的 ArrayList 容器类数据结构，叫做列表。通常我们把列表来作为 Python 中的数组使用。Python 中列表存储的数据类型可以不一致，数组长度也可以不一致。例如：

arr = ['python', 'java', ['asp', 'php'], 'c']

数组的优点与局限性¶

数组存储在连续的内存空间内，且元素类型相同。这种做法包含丰富的先验信息，系统可以利用这些信息来优化数据结构的操作效率。

空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
支持随机访问：数组允许在 �(1) 时间内访问任何元素。
缓存局部性：当访问数组元素时，计算机不仅会加载它，还会缓存其周围的其他数据，从而借助高速缓存来提升后续操作的执行速度。

连续空间存储是一把双刃剑，其存在以下局限性。

插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素。
长度不可变：数组在初始化后长度就固定了，扩容数组需要将所有数据复制到新数组，开销很大。
空间浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了

题目

438. 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

示例 2:

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

189. 轮转数组 rotate array

方法1: 创建新的数组

创建新的数组,使用额外的储存空间

python切片语法

列表切片语法：

基本形式：list[start:stop:step]
- start是切片开始的索引（包含该索引指向的元素），默认值为0。
- stop是切片结束的索引（不包含该索引指向的元素），默认值为列表长度。
- step是切片的步长，表示取元素的间隔，默认值为1。

使用`[:]`进行列表复制：

当你省略start和stop索引时（即[:]），切片操作会选取整个列表。
这种方式实现的是列表的浅拷贝，意味着列表本身被复制了，但是列表中的元素并没有被复制。如果列表中的元素是不可变类型（如整数、字符串等），这通常不会引起问题。但如果列表中包含可变对象（如其他列表），则原始列表和复制的列表中的可变元素将指向相同的对象。

example:

original_list = [1, 2, 3, 4]
copied_list = original_list[:]  # 创建 original_list 的一个浅拷贝# 修改 copied_list 不会影响 original_list
copied_list.append(5)
print(original_list)  # 输出: [1, 2, 3, 4]
print(copied_list)    # 输出: [1, 2, 3, 4, 5]

1. 暴力法3种写法

insert and pop

class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""res = nums[:] #创建列表副本：res = nums[:] 创建了nums的一个副本，名为res。这样做是为了在不改变原始列表的情况下，先在副本上进行修改。n=len(nums)for i in range(n):pos =(i+k)%nres[pos]=nums[i]for i in range(n):nums[i]=res[i]

计算新位置并填充到副本：
- n = len(nums) 获取列表nums的长度，存储在变量n中。
- 接着使用一个循环for i in range(n):来遍历nums中的每个元素。
  - 对于每个元素的索引i，计算它旋转k步后的新位置pos，这通过(i+k)%n得到。这里使用取模操作符%是为了处理k大于列表长度的情况，确保计算出的位置索引不会超出列表范围。
  - 然后将原始列表nums中索引为i的元素赋值给副本res中计算出的新位置pos。
将修改后的副本复制回原列表：
- 使用另一个循环for i in range(n):来遍历修改后的副本res。
- nums[i] = res[i]将副本res中的每个元素复制回原始列表nums的对应位置
时间复杂度： O(n) + O(n) + O(n) = O(n)
空间复杂度：O(n)

综合来看，这个旋转数组的方法是时间效率较高（线性时间复杂度），但在空间上并不是最优的，因为它需要额外的空间来存储整个数组的副本。在一些对空间敏感的场景下，可能需要考虑其他更节省空间的旋转方法。

2. 切片并拼接

class Solution:def rotate(self, nums: List[int], k: int) -> None:"""Do not return anything, modify nums in-place instead."""n = len(nums) #Gets the length of the nums list and stores it in n.k = k % n #Updates k to k % n to handle cases where k is greater than n. #This step ensures that the rotation count is within the range of the list's length.nums[:] = nums[n - k:] + nums[:n - k]

Rotating the List: The list is rotated by slicing and rearranging its elements:

nums[:] = nums[n - k:] + nums[:n - k]: This line is the key to rotating the list. It works as follows:
- nums[n - k:]: Takes a slice of the last k elements from the list.
- nums[:n - k]: Takes a slice of the first n - k elements from the list.
- nums[n - k:] + nums[:n - k]: Concatenates the last k elements with the first n - k elements, effectively rotating the list to the right by k steps.
- nums[:] =: Assigns the newly arranged list back to nums. Using nums[:] instead of nums for assignment modifies the list in place, meaning the original list passed to the function is changed outside the function as well.

综合来看，这个解法在时间复杂度上与前一个方法相同（都是O(n)），但在空间复杂度上更优（O(1) vs. O(n)），因为它避免了创建整个数组副本的需要。这使得它在空间使用上更为高效，特别是对于大数据量的情况。

2. reverse

class Solution:def rotate(self, nums: List[int], k: int) -> None:"""Do not return anything, modify nums in-place instead."""def reverse(l,r):while (l<r):nums[l],nums[r]= nums[r],nums[l]l += 1r -= 1n = len(nums)k = k % n #计算实际的旋转步数reverse(0, n-1) #翻转整个列表reverse(0, k-1) #翻转前k个元素reverse(k,n-1) #翻转剩余的元素

辅助函数`reverse`

reverse(l, r): 这个内部定义的函数用于翻转nums列表中索引从l到r（包含l和r）的元素。它通过一个while循环交换两端的元素，直到中间相遇

主方法`rotate`

计算实际的旋转步数：因为列表的长度可能小于旋转步数k，所以首先通过k = k % n计算实际需要旋转的步数（n是列表的长度）。这样做的目的是处理k大于列表长度的情况，确保旋转步数是有效的。
翻转整个列表：通过调用reverse(0, n-1)翻转整个列表。这个步骤是将列表看作是一个环，通过翻转来初始化旋转操作。
翻转前k个元素：然后通过reverse(0, k-1)仅翻转列表中前k个元素。由于整个列表在第一步中已经翻转过了，这一步实际上是将最初的后k个元素移动到了列表的前面。
翻转剩余的元素：最后，通过reverse(k, n-1)翻转索引从k到n-1的元素，即列表中剩余的部分。这一步将这部分元素恢复到正确的顺序。

示例

假设nums = [1,2,3,4,5,6,7]且k = 3，那么旋转的步骤如下：

原始列表：[1,2,3,4,5,6,7]
翻转整个列表：[7,6,5,4,3,2,1]
翻转前k个元素：[5,6,7,4,3,2,1]
翻转剩余的元素：[5,6,7,1,2,3,4]

最终结果是`[5,6,7,1,2,3,4]`，即将原始列表向右旋转了3步。

66. 加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

class Solution(object):def plusOne(self, digits):""":type digits: List[int]:rtype: List[int]"""s = '' #定义一个空字符串s，用于临时存储digits数组表示的数字。l = [] #定义一个空列表l，用于存储最终结果。for i in range(len(digits)):s += str(digits[i])s = str(int(s)+1)for i in s:l.append(int(i))return l

方法步骤详解

将数字数组转换为字符串：

通过一个循环for i in range(len(digits)):遍历digits数组。
s += str(digits[i])：将每个数字转换为字符串并附加到s上。这一步骤将数字数组如[1, 2, 3]转换为字符串"123"。

字符串数字加一：

s = str(int(s)+1)：将字符串s转换为整数并加一，然后再次转换为字符串。这一步处理了整数加一的操作。例如，如果s是"123"，加一后会变成"124"。

将结果字符串转换回数字数组：

再次使用循环for i in s:遍历字符串中的每个字符。
l.append(int(i))：将每个字符转换回整数并添加到列表l中。例如，如果s是"124"，则l将变为[1, 2, 4]。

返回结果：

return l返回列表l作为最终结果。

示例

假设输入digits = [1, 2, 3]，方法的执行过程如下：

将digits转换为字符串s = "123"。
将字符串表示的数字加一得到s = "124"。
将字符串s转换回数组l = [1, 2, 4]。
返回结果[1, 2, 4]。

724. 寻找数组的中心下标

示例 1：

输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。

class Solution:def pivotIndex(self, nums: List[int]) -> int:sum_left, sum_right = 0, sum(nums)for i in range(len(nums)):sum_right -= nums[i]# 若左侧元素和等于右侧元素和，返回中心下标 iif sum_left == sum_right:return isum_left += nums[i]return -1

方法步骤详解

初始化变量：
- sum_left, sum_right = 0, sum(nums)：sum_left用于存储当前索引左侧元素的和（初始值为0），sum_right用于存储整个数组的和，表示初始时右侧元素的总和。
遍历数组：
- 使用for i in range(len(nums)):遍历数组中的每个元素。变量i代表当前考虑的中心索引。
更新右侧和并检查条件：
- sum_right -= nums[i]：在每次循环开始时，从右侧元素和中减去当前元素，因为此元素将被考虑为中心索引的左侧部分。
- if sum_left == sum_right:：检查当前的左侧和是否等于右侧和。如果相等，说明找到了中心索引，直接返回该索引i。
更新左侧和：
- sum_left += nums[i]：将当前元素加到左侧和中，因为在下一次迭代中，当前元素将属于左侧部分。
遍历结束后：
- 如果遍历了整个数组都没有找到符合条件的中心索引，则返回-1。