从零开始：神经网络（2）—

声明：本文章是根据网上资料，加上自己整理和理解而成，仅为记录自己学习的点点滴滴。可能有错误，欢迎大家指正。

神经元相关知识，详见从零开始：神经网络——神经元和梯度下降-CSDN博客

1、什么是M-P 模型

人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多。那么神经网络是如何实现这种模拟的，并且达到一个惊人的良好效果的？这要由“飞鸟派”即仿生派说起。仿生派就是把进化了几百万年的生物，作为“模仿”对象，搞清楚原理后，再复现这些对象的特征。其实现在所讲的神经网络包括深度学习，都在某种程度上，属于“飞鸟派”——它们在模拟大脑神经元的工作机理。追根溯源，模仿神经元的“飞鸟”实例，就是上世纪40年代提出但一直沿用至今的“M-P神经元模型”。

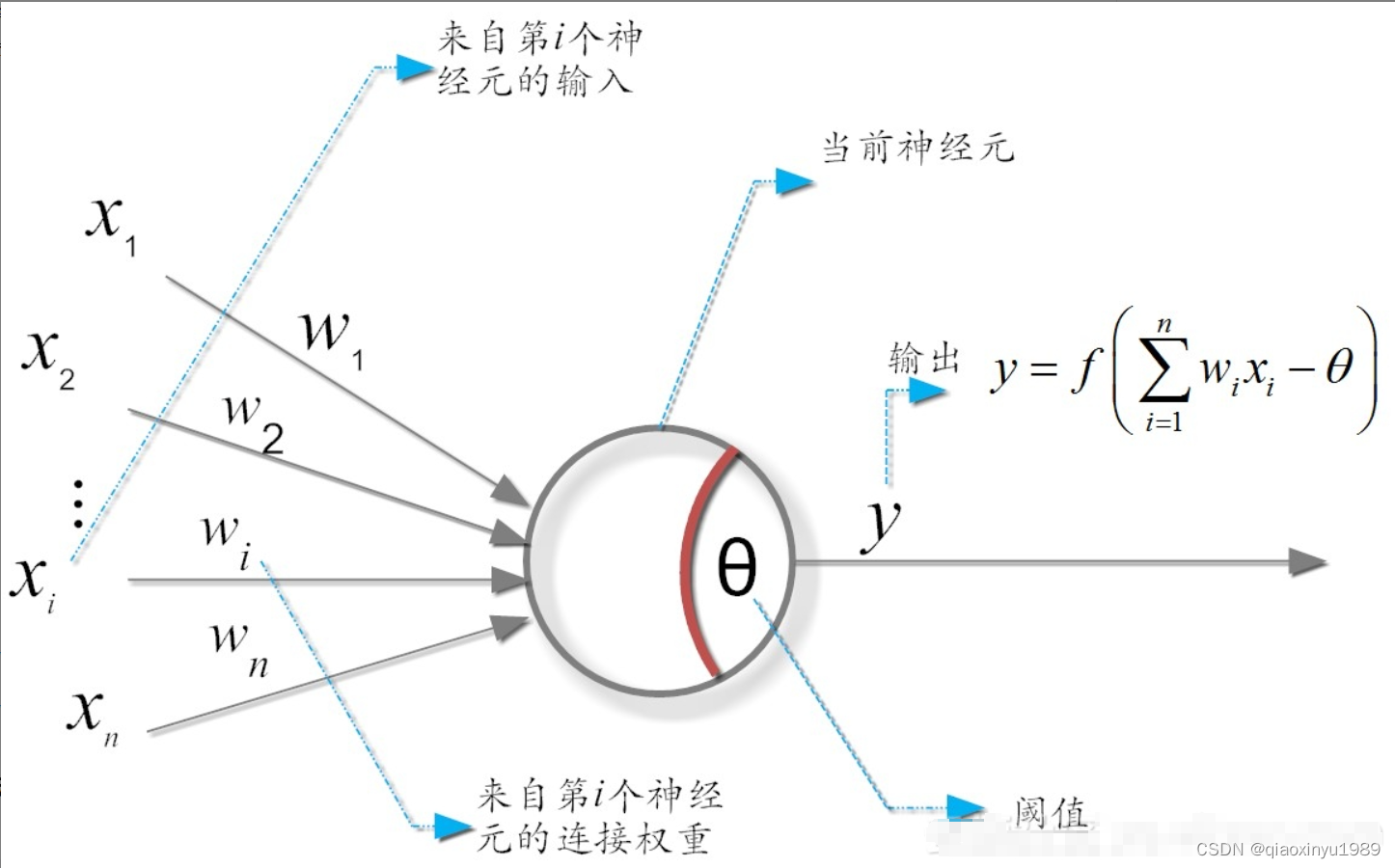
1943年，由美国心理学家麦卡洛克(McCulloch, W. S. )和数学家皮特斯((Puts , W.) 按照生物神经元，建立起了著名的阈值加权和模型，即麦卡洛克-皮特斯模型（McCulloch-Pitts model），简称为M-P模型，其拓扑结构便是现代神经网络中的一个神经元。

在这个模型中，神经元接收来自n个其它神经元传递过来的输入信号x（图中 $x_{1}$ ~ $x_{n}$ ），这些信号的表达，通常通过神经元之间连接的权重w（图中 $w_{1}$ ~ $w_{n}$ ）大小来表示，神经元将接收到的输入值按照某种权重叠加起来，并将当前神经元的阈值θ进行比较，然后通过“激活函数（activation function）”f（）向外表达输出，如图所示。

即

M-P模型的工作原理为：当所有的输入与对应的连接权重的乘积大于阈值 $\theta$ 时,y输出为1，否则输出为0。即当 $w_{i}*x_{i}>\theta$ ， $y=1$ ；否则 $y=0$ 需要注意的是， $x_{i}$ 也只能是0或1的值，而权重 $w_{i}$ 和 $\theta$ 则根据需要自行设置。

简单吧？很简单！但是还是看不懂，下面举例说明

2、M-P数学表达式

如下图所示，假设某个模型：包含有3个输入，1个输出，以及2个计算功能。注意中间的箭头线。这些线称为“连接”（神经元中最重要的东西）。每个上有一个“权值”。

一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。

举个例子，如果我们已知张三，李四重多少，想让神经网络输出两个人受到的重力加在一起是多少。我们其实知道关于重力的公式 $G=m*g$ ，但是这个单层神经网络并不知道，那么怎么让他学习到这个关系呢？假设我们统计了很多个数据（输入），每个数据包含第一个人重 $m_{1}$ kg，第二个人的重 $m_{2}$ kg，以及他们一起的重力 $output$ （输出）。我们将这些数据丢给神经网络去学习，它最终会学习（调整）两个参数 $w_{1}$ ， $w_{2}$ （权值），逼近于 $g$ 的值。所以可以用这个数学公式来表示：

$output=\sum m_{i}*w_{i}$

但此时，神经网络还只能做到线性的变换。但是其实在现实生活中很多问题，输入和输出不是线性的关系的。比如一个狗狗图片，我们人眼看到它，大脑会分辨出这是一只狗。其中狗狗图片就是输入，这是一只狗是输出，其中大脑处理的过程肯定不是线性的变换。那怎么办？

神经网络通过激活函数 $\sigma$ （也就是上图的非线性函数）来实现了这个非线性变换。你可能会问一个激活函数就有这么大的作用吗？就好比0和1一样，基于它们才有了我们现在的计算机，它甚至构造了整个虚拟世界。同样，如果有多个单层神经元组合起来，再加上可学习的参数调整，它能做的事情会很多，甚至出乎你的意料。最终上面的数学公式变成了：

$output=\sigma (\sum m_{i}*w_{i})$

下面，我们使用a来表示输入，用w来表示权值。一个表示连接的有向箭头可以这样理解：在初端，传递的信号大小仍然是a，端中间有加权参数w，经过这个加权后的信号会变成a*w，因此在连接的末端，信号的大小就变成了a*w。如果我们将神经元图中的所有变量用符号表示，并且写出输出的计算公式的话，就是下图：

　可见z是在输入和权值的线性加权和叠加了一个函数g的值。在M-P模型里，函数g是sgn函数（sgn是英文sign(标记)的缩写），即符号函数（sign function）。这个函数当输入大于0时，输出1，否则输出0。即

下面对神经元模型的图进行一些扩展。首先将sum函数与sgn函数合并到一个圆圈里，代表神经元的内部计算。其次，把输入a与输出z写到连接线的左上方，便于后面画复杂的网络。最后说明，一个神经元可以引出多个代表输出的有向箭头，但值都是一样的。神经元可以看作一个计算与存储单元。计算是神经元对其的输入进行计算功能。存储是神经元会暂存计算结果，并传递到下一层。

　　当我们用“神经元”组成网络以后，描述网络中的某个“神经元”时，我们更多地会用“单元”（unit）来指代。同时由于神经网络的表现形式是一个有向图，有时也会用“节点”（node）来表达同样的意思。

　需要说明的是，至今为止，我们对神经网络的结构图的讨论中都没有提到偏置节点（bias unit）。事实上，这些节点是默认存在的。它本质上是一个只含有存储功能，且存储值永远为1的单元(即相当于输入a0=1，如下图中的+1)。在神经网络的每个层次中，除了输出层以外，都会含有这样一个偏置单元。那么，为什么要存在偏置呢？

从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值（阈值 $\theta$ ）时，神经元细胞才会处于兴奋状态，即当：

$w_{1}*x_{1}+w_{2}*x_{2}+w_{3}*x_{3}\geqslant \theta$

时，该神经元细胞才会兴奋。我们把 $\theta$ 挪到等式左侧来，变成 $-\theta$ ，然后把它写成 b ，变成了：

$w_{1}*x_{1}+w_{2}*x_{2}+w_{3}*x_{3}+b\geqslant 0$

于是偏置 b就诞生了！亦即，我们可以得到神经元的数学/计算模型如下所示:

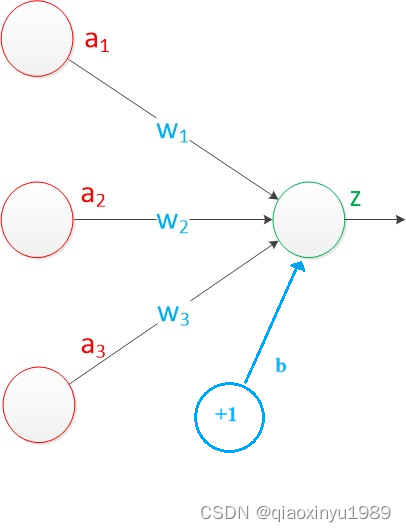
可以看出，偏置节点很好认，因为其没有输入（前一层中没有箭头指向它）。有些神经网络的结构图中会把偏置节点明显画出来，有些不会。一般情况下，我们都不会明确画出偏置节点。

在考虑了偏置以后上图的神经网络的矩阵运算为： $z=g(\sum w_{i}*a_{i}+b)$

（1）单个神经元的MP数学公式

则单个神经元的MP模型为：

$y=f(x)=sgn(x)=\sigma ( \sum_{i=1}^{m} w_{i}*x_{i}+b)$

其中，输入 $x_{i}(i=1,2,...,m)$ :表示第 i个输入变量(自变量)，m为输入变量的个数
输入 $w_{i}(i=1,2,...,m)$ :表示第 i个权重，与相同下标的 $x_{i}$ 相对应
输入 $b$ 表示偏置
输出 $y$ 表示输出变量(因变量)
$\sigma(.)$ 表示一个激活函数，它对线性加权求和的结果进行非线性变换

把矩阵上的输入（实数值向量）映射到输出值 $f(x)$ 上（一个二元值）,其数学表达式为：

$f(x)=\left\{\begin{matrix} 1&,if&x\geqslant 0, \\ 0&,if&x<0\end{matrix}\right.$ 式子（1）

（2）单个神经元的MP数学公式

如果将多个神经元的MP模型统一编号，可以表示成一个式子：

$y_{k}=\sigma ( \sum_{i=1}^{m} w_{ki}*x_{i}+b_{k})$

其中，输入 $x_{i}(i=1,2,...,m)$ :表示第 i个输入变量(自变量)，m为输入变量的个数
输入 $w_{ki}(k=1,2,...,n,i=1,2,...,m)$ :表示第 $k$ 个神经元的第 i个权重
输入 $b_{k}$ 表示第 $k$ 个神经元的偏置
输出 $y_{k}(k=1,2,...,n)$ 表示第 $k$ 个神经元的输出变量(因变量)
n表示神经元的个数

3、M-P模型逻辑规则的应用

（1）非运算

非运算是单输入和单输出，结构图如下：

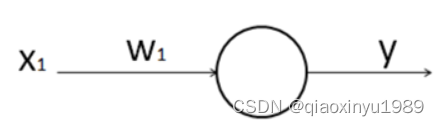
则其表达式为： $y=f(x)=\sigma (w_{1}*x_{1}+b)$

运算原理：

$x_{1}$

$x=w_{1}*x_{1}+b$

代入求值的x=

$y$

根据sgn(x)的规则（见式子1），

可得偏置b取值范围

$b$

$b\geqslant 0$

即： $0\leqslant b<-w_{1}$

$w_{1}+b$

$b<-w_{1}$

如：可取 $b= 1, w_{1}= -2$ ,均满足b的取值范围，则 $y=f(x)=\sigma (-2*x_{1}+1)$

（2）或运算

或运算以两个输入为例，结构图如下：

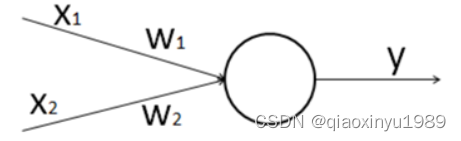
则其表达式为： $y=f(x)=\sigma (w_{1}*x_{1}+w_{2}*x_{2}+b)$

运算原理：

$x_{1}$	$x_{2}$	$x=w_{1}x_{1}+w_{2}x_{2}+b$ 代入求x的值	$y$	根据sgn(x)的规则（见式子1），可得偏置b取值范围
0	0	$b$	0	$b< 0$	$max{\begin{Bmatrix} -(w_{1}+w_{2}),-w_{1},-w_{2} \end{Bmatrix}}\leqslant b< 0$
0	1	$w_{2}+b$	1	$b\geqslant -w_{2}$
1	0	$w_{1}+b$	1	$b\geqslant -w_{1}$
1	1	$w_{1}+w_{2}+b$	1	$b\geqslant -(w_{1}+w_{2})$

如：可取 $w_{1}= 1,w_{1}= 1,b= -0.5$ ,均满足b的取值范围，则 $y=f(x)=\sigma (1*x_{1}+1*x_{1}-0.5)$

（3）与运算

逻辑与运算与逻辑或一致，把运算原理改改即可：

运算原理：

$x_{1}$	$x_{2}$	$x=w_{1}x_{1}+w_{2}x_{2}+b$ 代入求x的值	$y$	根据sgn(x)的规则（见式子1），可得偏置b取值范围
0	0	$b$	0	$b< 0$	$-(w_{1}+w_{2})\leqslant b< min\begin{Bmatrix}0,-w_{1},-w_{2} \end{Bmatrix}$
0	1	$w_{2}+b$	0	$b< -w_{2}$
1	0	$w_{1}+b$	0	$b<-w_{1}$
1	1	$w_{1}+w_{2}+b$	1	$b\geqslant -(w_{1}+w_{2})$

如：可取 $w_{1}= 1,w_{1}= 1,b= -1.5$ ,均满足b的取值范围，则 $y=f(x)=\sigma (1*x_{1}+1*x_{1}-1.5)$

（4）异或运算（不能实现）

仍然以二输入为例：表达式为： $y=f(x)=\sigma (w_{1}*x_{1}+w_{2}*x_{2}+b)$

运算原理：

$x_{1}$	$x_{2}$	$x=w_{1}x_{1}+w_{2}x_{2}+b$ 代入求x的值	$y$	根据sgn(x)的规则（见式子1），可得偏置b取值范围
0	0	$b$	0	$b< 0$	因为既要大于 $-w_{1}$ ， $-w_{2}$ 又要小于 $-(w_{1}+w_{2})$ ，b是无解的。
0	1	$w_{2}+b$	1	$b\geqslant -w_{2}$
1	0	$w_{1}+b$	1	$b\geqslant -w_{1}$
1	1	$w_{1}+w_{2}+b$	0	$b< -(w_{1}+w_{2})$