【题目描述】
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
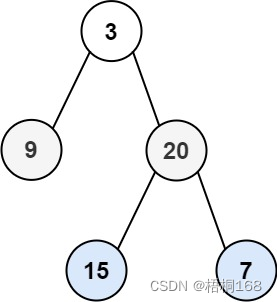
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
【题目链接】. - 力扣(LeetCode)
【解题代码】
package tree.binarytree;import java.util.*;public class LevelOrderTraversal {public static void main(String[] args) {Integer[] array = new Integer[]{1,2,3,4,null,null,5};TreeNode root = TreeNode.constructTree(array);List<List<Integer>> lists = new LevelOrderTraversal().levelOrder(root);lists.forEach(l -> System.out.println(Arrays.toString(l.toArray())));}private List<List<Integer>> levelOrder(TreeNode root) {// 特殊情况处理,如果树根节点为空,返回空列表if (root == null) return new ArrayList<>();// 定义一个队列,临时存放所访问的树节点Queue<TreeNode> queue = new LinkedList<>();// 首先将树的根节点放入队列中queue.add(root);TreeNode node;// 存储所有层节点列表的列表List<List<Integer>> lists = new ArrayList<>();// 初始化当前父节点个数为1(即根节点),以及子节点个数int curLevelCount = 1, nextLevelCount = 0;// 当前层节点列表List<Integer> list = new ArrayList<>();while (curLevelCount > 0) {// 从队列里弹出一个父节点,并将父节点数据减1node = queue.poll();curLevelCount--;// 将此父节点放入当前层节点列表list.add(node.val);// 如果此节点左子节点不为空,放入队列中,并将子节点数目加1if (node.left != null) {queue.add(node.left);nextLevelCount++;}// 如果此节点右子节点不为空,放入队列中,并将子节点数目加1if (node.right != null) {queue.add(node.right);nextLevelCount++;}// 如果当前层父节点访问完毕if (curLevelCount == 0){// 将当前层节点,拷贝到结果列表中,并进行清空lists.add(new ArrayList<>(list));list.clear();// 然后将下一层所有节点作为当前层节点,重启新一轮的遍历curLevelCount = nextLevelCount;nextLevelCount = 0;}}// 最后返回结果return lists;}
}【解题思路】
我们之前数据结构学习树遍历的内容,一般都是左、中、右三种遍历循序,按树的层次遍历还没处理过,需要自行思考,不能借鉴教科书了,深入反复思考,得出以下几个要点
- 第一层就一个节点,树的根节点,第二层就是根节点的左右子节点,第三层就是根节点的左右子节点的所有左右子节点,后面以此类推。。。
- 每次我们可以在队列中保存当前层的树节点,然后一一弹出,放入当前层列表中,并将其子节点放入队列中
- 当前层访问结束后,剩下的就是当前层的下一层所有节点。将其设置为新的当前层,反复循环处理即可
按照这个思路,很快就写出算法代码,并提交成功,解题步骤如下:
【解题步骤】
- 定义当前层树节点列表以及结果所有层节点列表
// 定义一个队列,临时存放所访问的树节点 Queue<TreeNode> queue = new LinkedList<>(); // 存储所有层节点列表的列表 List<List<Integer>> lists = new ArrayList<>(); - 定义一个队列,临时存放所访问的树节点,首先将树的根节点放入队列中
// 定义一个队列,临时存放所访问的树节点 Queue<TreeNode> queue = new LinkedList<>(); // 存储所有层节点列表的列表 queue.add(root); - 初始化当前父节点个数为1(即根节点),以及子节点个数
int curLevelCount = 1, nextLevelCount = 0; - 依次遍历当前层所有节点,一一从队列里弹出,放入当前层节点列表
while (curLevelCount > 0) {// 从队列里弹出一个父节点,并将父节点数据减1node = queue.poll();curLevelCount--;// 将此父节点放入当前层节点列表list.add(node.val); - 将其左右子节点作为下一层节点加入队列中
// 如果此节点左子节点不为空,放入队列中,并将子节点数目加1 if (node.left != null) {queue.add(node.left);nextLevelCount++; } // 如果此节点右子节点不为空,放入队列中,并将子节点数目加1 if (node.right != null) {queue.add(node.right);nextLevelCount++; } - 如果当前层所有节点遍历完毕,将当前层节点,拷贝到结果列表中,并进行清空,然后将下一层所有节点作为当前层节点,重启新一轮的遍历
// 如果当前层父节点访问完毕 if (curLevelCount == 0){// 将当前层节点,拷贝到结果列表中,并进行清空lists.add(new ArrayList<>(list));list.clear();// 然后将下一层所有节点作为当前层节点,重启新一轮的遍历curLevelCount = nextLevelCount;nextLevelCount = 0; } - 最后返回结果
return lists;
【思考总结】
- 这道理的关键点在于“自顶向下,一层接一层交替访问树节点”;
- 算法设计时,可以考虑最简单的情况,试探思考其运行逻辑应该是什么样的
- 还是要有精细化的逻辑思维,层次分明,这样在复杂的逻辑也不会乱;
- LeetCode解题之前,可以看提示,但一定不要看题解,看了就“破功”了!


![[机器视觉]halcon应用实例 找圆](https://img-blog.csdnimg.cn/direct/d9a82e38836842378c8c1a826c0b6d32.png)