1.二分查找

1.1题目

704.二分查找—力扣题目链接

• 题目：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
• 示例一：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

• 示例二：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

1.2思路（核心：区间的定义）

1. 题目的前提是数组为有序数组，同时题目还强调 数组中无重复元素
2. 因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

1.3左闭右闭

• 定义target在 [left, right] 区间，所以有如下两点：

1. while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
2. if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
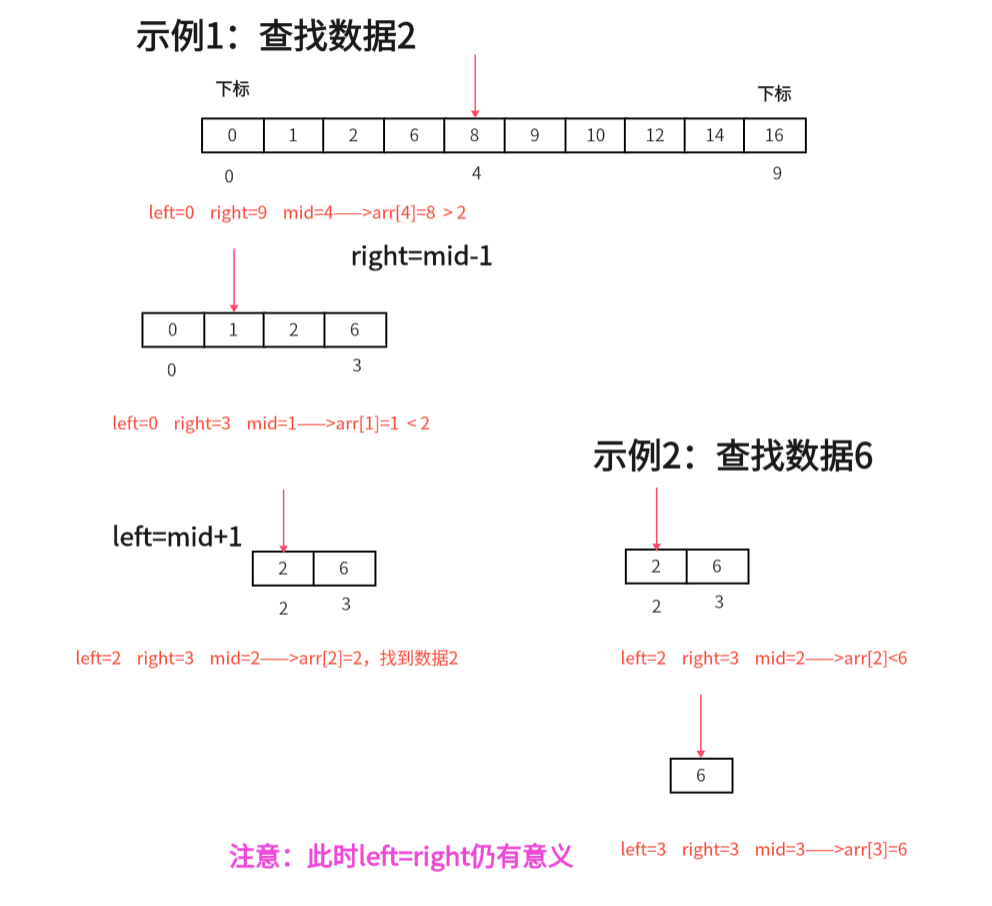
3. 下面举例演示：在一组有序，不重复数组中分别查找数据2、数据6的过程

/*** @Description 二分查找第一种写法：左闭右闭* @Param* @Return 下标值：int*/public int binarySearch1(int[] arr,int target){int left=0;int right=arr.length-1;while(left<=right){/***  写法一：可能出现溢出情况*      int mid=(left+right)/2;*  写法二：*      int mid=left+(right-left)/2;*///写法三：右移运算符 代替 除号int mid=left+((right-left)>>1);if(arr[mid]>target){        //在左区间，即[left,mid-1]right=mid-1;}else if(arr[mid]<target){  //在右区间，即[mid+1,right]left=mid+1;}else{return mid;}}return -1;}

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

1.4左闭右开

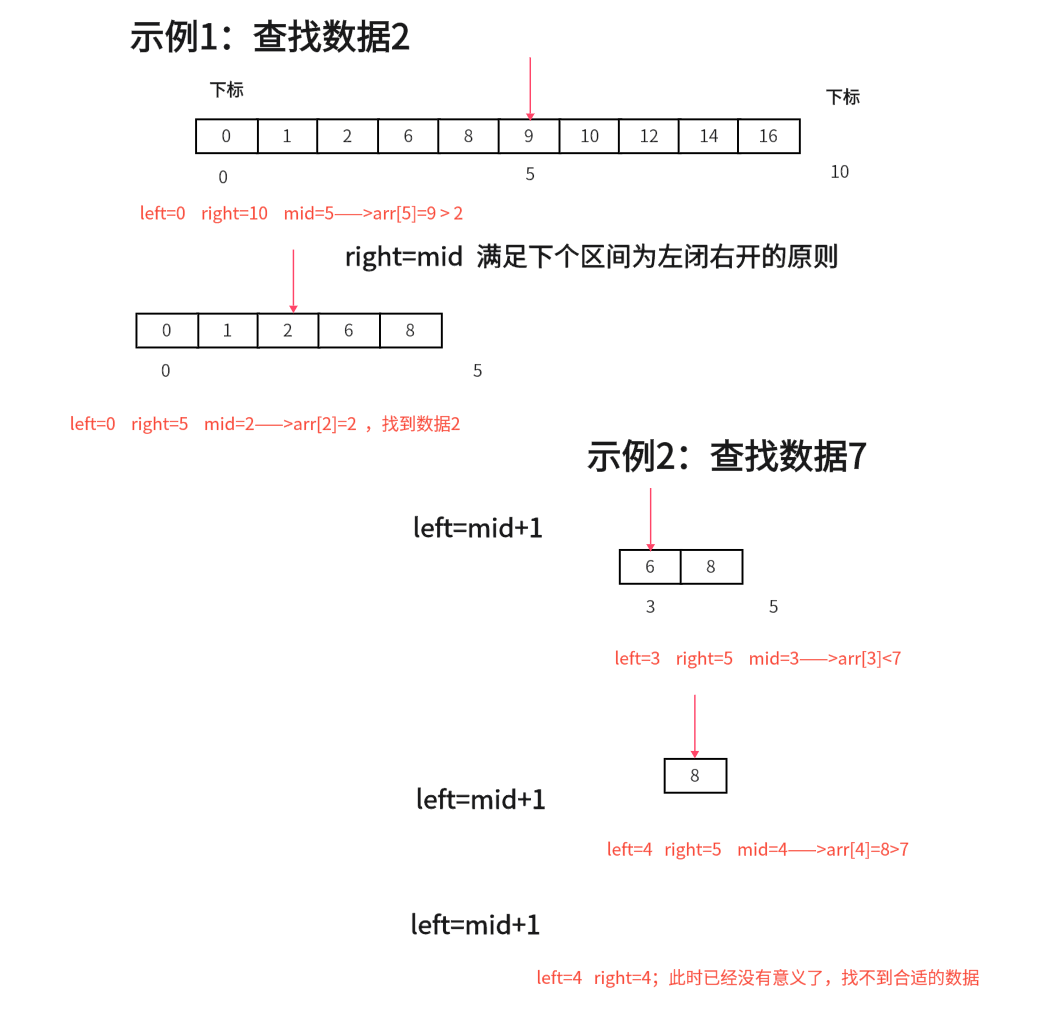
如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

1. while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
2. if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]大于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

• 代码示例：

	/*** @Description 二分查找第一种写法：左闭右闭* @Param* @Return 下标值：int*/public int binarySearch2(int[] arr,int target){int left=0;int right=arr.length;while(left<right){int mid=left+((right-left)>>1);if(arr[mid]>target){        //在左区间，即[left,mid-1)right=mid;}else if(arr[mid]<target){  //在右区间，即[mid+1,righ)left=mid+1;}else{return mid;}}return -1;}

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

1.5总结

• 使用二分查找的两个前提：
  • 数组有序
  • 数组元素唯一，不重复
• 二分查找的两个写法区分：

	左闭右闭	左闭右开
right初始取值	right=arr.length-1	right=arr.length
循环条件	while(left<=right)	while(left<right)
left更新值（到右区间查找）	left=mid+1	left=mid+1
right更新值（到左区间查找）	right=mid-1	right=mid