基础知识:方差,协方差,协方差矩阵
方差:描述了一组随机变量的离散程度
方差= 每个样本值 与 全部样本的平均值 相差的平方和 再求平均数,记作:

例如:计算数字1-5的方差,如下

去中心化:为了后续计算的方便,会对样本进行去中心化处理,方法是将全部样本按照平均值平移
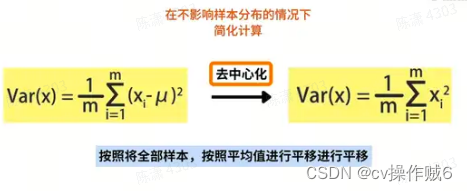
例如:1-5每个数字都向负方向移动3(平均值)个单位,计算方差后结果依然是2

协方差:协方差描述了不同特征之间的相关情况,通过计算协方差,可以判断不同特征之间的关联关系。协方差=m个样本的(特征a-均值ua )乘以(特征b - 均值 ub)的乘积累加到一起再除以m-1

例如1:一组数据点(1,1)(2,2)(3,3)(4,4)(5,5)他们的协方差计算如下

例如2:同理

例如3:同理

为了更方便的计算协方差,同样的也可以将数据去中心化处理

总之:协方差表示了不同特征之间的相关情况,想个特征值之间的协方差>0,则正相关,<0则负相关,=0则不相关
协方差矩阵:计算了不同维度的协方差,他是一个对对称矩阵,由方差和协方差两部分组成,其中,对角线上的元素是各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差。


在计算协方差矩阵时,需要将m个样本的特征按照列向量的方式,保存在矩阵中,然后计算矩阵和矩阵转置的乘积,再除以m,得到协方差矩阵
例如:m个样本,每个样本有a和b两个特征,将这些样本按照列向量的方式,保存到矩阵x中,计算m个样本的协方差矩阵,他等于x乘以x的转置,再除以m。

1.SVD求解ICP方法C++代码展示,总结起来分为3步

#include<iostream>
#include<vector>
#include<eigen>
using namespace std;
//函数用于估计两组三维点集之间的旋转矩阵 R 和平移向量 t
//通过这段代码,可以实现对两组三维点集之间的姿态关系进行估计和计算,其中旋转矩阵R_用于描述旋转关系,平移向量t_用于描述平移关系
void pose_estimation_3d3d(const vector<Point3f>& pts1,const vector<Point3f>& pts2,Mat& R, Mat& t)
{// 计算两组三维点的质心Point3f p1, p2;int N = pts1.size();for (int i=0; i<N; i++){p1 += pts1[i];p2 += pts2[i];}p1 /= N;p2 /= N;// 对每个减去质心,得到新的点集q1,q2vector<Point3f> q1(N), q2(N);for (int i=0; i<N; i++){q1[i] = pts1[i] - p1;q2[i] = pts2[i] - p2;}// 计算协方差矩阵3x3 q1*q2^TEigen::Matrix3d W = Eigen::Matrix3d::Zero();for (int i=0; i<N; i++){W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x,q2[i].y, q2[i].z).transpose();}cout << "W=" << W << endl;// SVD on W 对矩阵 W 进行奇异值分解(SVD)得到 U 和 V 矩阵。Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);Eigen::Matrix3d U = svd.matrixU();Eigen::Matrix3d V = svd.matrixV();cout << "U=" << U << endl;cout << "V=" << V << endl;//根据计算出的 U 和 V 矩阵计算旋转矩阵 R 和平移向量 t。Eigen::Matrix3d R_ = U * (V.transpose());Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);//p1 p2分别为两组数据的中心点//将计算得到的旋转矩阵 R 和平移向量 t 转换为 OpenCV 的 Mat 类型。// convert to cv::MatR = (Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0,2),R_(1, 0), R_(1, 1), R_(1,2),R_(2, 0), R_(2, 1), R_(2,2));t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}经过上面的步骤,其实就可以得到R和T了,但是,这时候就出现了一个问题——结果不准确。在算法实现中,如果出现了求解值不准确的情况,那么一般做法就是——多求几次,也就是迭代!可以参考如下:
- 从B点云中一一找到A中点的对应距离最近点,构成最近点集C
- 把C点集存入Eigen矩阵中,和A点云去中心化后,求SVD分解,得到R矩阵和T向量(一个旋转一个平移)
- 开始迭代,通过R×A+T得到新的点云A1
- 重新执行1到3步骤,这次是从B中找A1的最近点
- 求得到的点云An和它的最近点集Cn的平均距离dst,当dst小于设定的阈值时,跳出循环
如果发现还不准确,那么有可能是它的迭代条件——也就是平均距离dst判断出错了,出现这种原因一般就是点云中出现了离散点,导致某两点的距离出现了异常,带动了整个dst判断出错。解决方案如下(很管用):
- 遍历A点找寻最近点,如果A中的某个点Ai和它的最近点距离大于某个阈值,则剔除,不参与接下来的计算。
- 从B点云中一一找到A中点的对应距离最近点,构成最近点集C
- 把C点集存入Eigen矩阵中,和A点云去中心化后,求SVD分解,得到R矩阵和T向量(一个旋转一个平移)
- 开始迭代,通过R×A+T得到新的点云A1
- 重新执行1到4,每次执行都要剔除一下离散点。
- 求得到的点云An和它的最近点集Cn的平均距离dst,当dst小于设定的阈值时,跳出循环
2.非线性优化求解ICP c++代码展示
#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
using namespace cv;#include <Eigen/Core>
#include <Eigen/SVD>
#include <Eigen/Dense>#include <chrono>
#include <sophus/se3.hpp>#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/sparse_optimizer.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/solver.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
using namespace std;
//定义VertexPose顶点 //顶点为6个优化变量,每个类型为SE3d(表示三维空间中的刚体变换,即旋转和平移)
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;// 设置初始化的更新值 virtual void setToOriginImpl() override { _estimate = Sophus::SE3d();}// left multiplication on SE3virtual void oplusImpl(const double *update) {Eigen::Matrix<double, 6, 1> update_eigen;//前三个元素表示平移在 x、y、z 轴上的分量,后三个元素表示旋转的绕 x、y、z 轴的旋转量update_eigen << update[0], update[1], update[2],update[3], update[4], update[5];_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;//exp 将update_eigen向量转换成SE3d 类型的刚体变换}virtual bool read(std::istream &in) override {return true;}virtual bool write(std::ostream &out) const override { return true;}
};
//定义边 一元边,连接一个顶点VertexPose ,和一个包含三维向量的观测
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, bcv::VertexPose>
{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}virtual void computeError() override {const VertexPose* p = static_cast<const VertexPose*> (_vertices[0]);//真实观测值 _measurement 与 估计观测值 p->estimate() * _point之间的误差_error = _measurement - p->estimate() * _point;//将顶点的估计值所代表的变换作用于点 _point,得到的新的位置信息}//linearizeOplus 函数实现了对雅可比矩阵的线性化操作virtual void linearizeOplus() override {VertexPose *p = static_cast<VertexPose*> (_vertices[0]);//从图优化中获取与当前边相连的顶点Sophus::SE3d T = p->estimate();//获取顶点的估计值(优化变量,用于计算位姿变换)Eigen::Vector3d xyz_trans = T * _point;//通过估计的值 计算当其点_point转换后的坐标//雅可比矩阵从 (0,0) 开始的 3×3 子矩阵(前三行前三列),设置为负的单位矩阵,表示误差函数对位姿变量的平移部分的导数_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();//雅可比矩阵的前三行后三列部分,利用 Sophus 库的 hat 操作将向量 xyz_trans 转换为反对称矩阵,通常表示误差函数对位姿变量的旋转部分的导数_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);}bool read(std::istream &in) { return true; }bool write(std::ostream &out) const { return true; }protected:Eigen::Vector3d _point;
};
//定义求解器
void ICPSolver::NLOSolver(std::vector<cv::Point3f> &pts1,std::vector<cv::Point3f> &pts2,cv::Mat &R, cv::Mat &t)
{typedef g2o::BlockSolverX BlockSolverType;//优化问题求解器typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;//稠密线性方程求解类型// new一个 g2o优化器 采用高斯牛顿优化算法auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));//构建优化问题的图模型g2o::SparseOptimizer optimizer; // graph modeloptimizer.setAlgorithm(solver); // set solveroptimizer.setVerbose(true); // print info//添加顶点bcv::VertexPose *p = new VertexPose();p->setId(0);//顶点idp->setEstimate(Sophus::SE3d());//初始估计值optimizer.addVertex(p);//添加边for(size_t i = 0; i < pts1.size(); i++) {bcv::EdgeProjectXYZRGBDPoseOnly *e = new bcv::EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));e->setVertex(0, p);//将上一步的顶点设置为边e的第一个顶点,本次只有一个顶点e->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));//设置了边的测量值(实际位置)e->setInformation(Eigen::Matrix3d::Identity());//设置边的信息矩阵为单位矩阵,表示边的置信度optimizer.addEdge(e);}auto t1 = std::chrono::system_clock::now();optimizer.initializeOptimization();//初始化优化器optimizer.optimize(100);//迭代次数auto t2 = std::chrono::system_clock::now();auto d = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1).count();std::cout << "duration: " << d << " ms" << std::endl;std::cout << "after optim:\n";std::cout << "T=\n" << p->estimate().matrix() << std::endl;Eigen::Matrix3d R_ = p->estimate().rotationMatrix();//estimate()提取估计值,rotationMatrix()提取旋转矩阵Eigen::Vector3d t_ = p->estimate().translation();//提取平移向量std::cout <<"det(R_)=" << R_.determinant() << std::endl;std::cout <<"R_R_^T=" << R_ * R_.transpose() << std::endl;std::cout << "R:\n" << R_ << std::endl;std::cout << "t:\n" << t_ << std::endl;R = (cv::Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0, 2),R_(1, 0), R_(1, 1), R_(1, 2),R_(2, 0), R_(2, 1), R_(2, 2));t = (cv::Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}