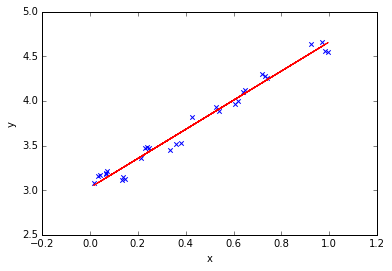
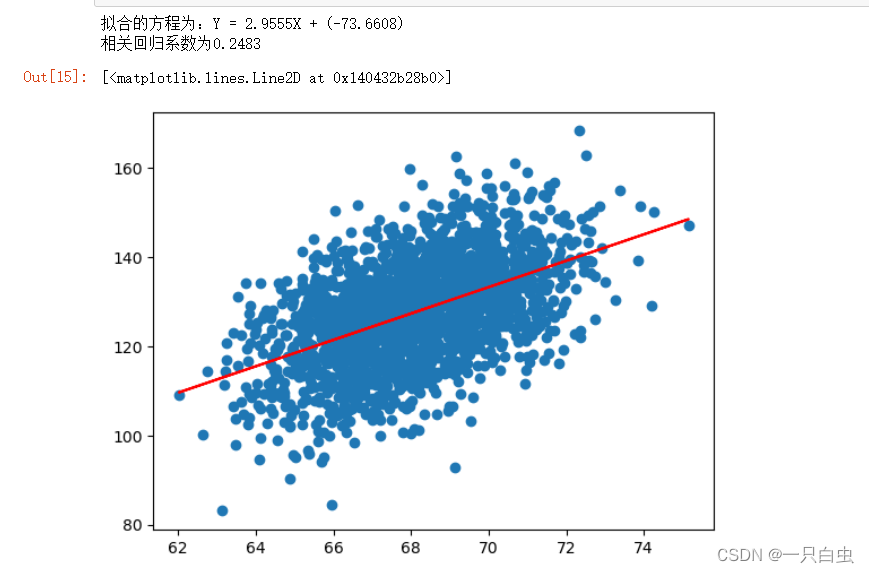
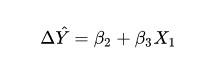上一篇我们详细的讲解了一元一次线性回归算法，今天我们接着上一篇，为大家讲解多元线性回归是怎么一回事。

何为多元？当我们的输入x只有一维属性时，我们称之为一元。就像我们判断人胖瘦，只需了解体重这一个属性，我们就可以辨识。当x包含n个属性，由n个属性进行描述时，我们称之为多元。比如我们判断一个西瓜是好瓜还是坏瓜，我们需要了解的信息就多了，我们需要知道瓜的生产日期，瓜的颜色，瓜敲起来声响如何等等，综合上述多种属性才能判断瓜的成色。这就是多元。

在多元线性回归中，我们的输入x可描述成如下所示，它表示一条样本数据有d个属性

同一元线性回归一样(注：这里不明白的可翻看上一篇推送)，我们需要做的就是寻找d维列向量w和常数b，解出方程：

由于输入样本x是多维的，计算起来可能有些困难，所以在这里我们使用一些小trick。我们把常数b 放入权值向量 w 中得到一个 (d+1) 维的权值向量 w^=(w;b)，w^=[w1,w2...wd,b]。相应的，我们把输入表示成一个矩阵X,其中每行对应一个样本，该行的前d个元素对应样本的d个属性值，最后一个元素恒置为1。我们假设样本有m个，则X可表示成：

那么X乘以w^就等于：

与我们目标函数的形式一致。

同一元线性回归一样，接下来我们需要求解下述函数的最小值

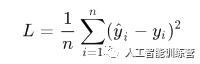
由于y-Xw^是一个列向量，平方就是两个列向量的乘积。为了方便计算，我们使用列向量转置(行向量)乘以列向量的形式，其计算结果同两个列向量乘积一样：

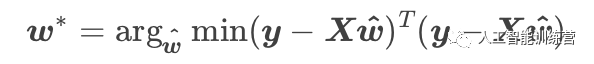
现在我们要做的就是最小化目标函数，因此需要对其求导，

根据向量求导公式

我们可得出：

上式中第一项中 yT 与 w^ 无关，所以结果为0。接下来计算第二项，根据行向量对列向量的求导公式，我们可以推出

因此上式结果第一项和第二项分别为

最终可得

令此式为0，当X的转置乘以X为满秩矩阵时可逆，因此可求解出w

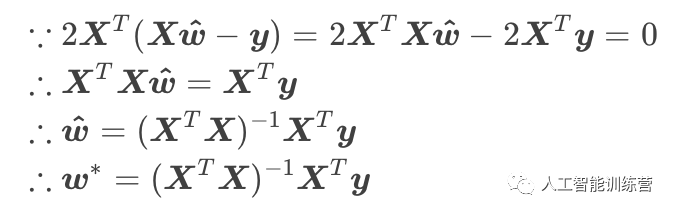
多元线性回归模型就为大家讲解到这里，下一篇讲解如何使用梯度下降法来求解线性回归模型，敬请期待哦！

希望一起交流学习～