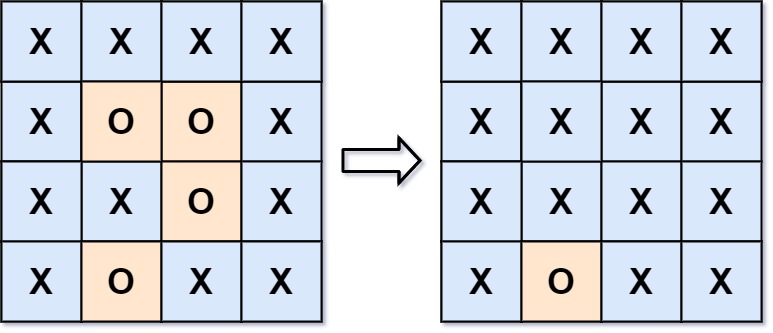
[ABC206E] Divide Both 解题记录

---

题意简述

给定整数 $L,R$，求满足以下条件的数对 $(x,y)$ 的数量。

• $x,y$ 不互质
• $x\nmid y$ 且 $y\nmid x$

---

题目分析

正难则反，考虑用所有的满足第一条性质的数对的数量减去不满足第二条性质的数量。
容易想到，如果不考虑第二条性质，那么我们可以枚举因子 $i\in [2,r]$，求解出 $[l,r]$ 区间内的 $i$ 的倍数的个数 $s$，然后用加法原理，两两配对，累加到答案中。
如何求解 $s$？
不妨设 $x=k\times i+b$，则 $i\mid (x-b)$，即对于每个 $j\in [1,k]$ 都有 $i\mid (x-b-j\times i)$，一共 $k$ 个数，而这个 $k$ 就是 $\lfloor \frac{r}{i}\rfloor$，对于 $k$ 个数字两两配对，即可求解出 $s=\frac{k\times (k-1)}{2}$。但是这样会有重复，如：当 $i=2,3,6$ 时，均会有数对 $(6,12)$，这个时候就需要我们标记了。可以设 $cn{t}_i$ 表示 $i$ 的质因子的个数，如果 $cn{t}_i$ 为偶数，就减去当前贡献，否则加上。那么我们对于 $i=2,3$ 的时候加上了$(6,12)$ 的贡献，在 $i=6$ 的时候就会减去一个，这样就保证了贡献不会重复（不清楚的可以手模）。
最后减去不满足第二条限制的贡献：对于每个因子 $i\in [2,r]$，减去 $[l,r]$ 中除 $i$ 外 $i$ 的倍数，即：$\lfloor \frac{r}{i}\rfloor -1$。

---

AC Code

#include<bits/stdc++.h>
#define arrout(a,n) rep(i,1,n)std::cout<<a[i]<<" "
#define arrin(a,n) rep(i,1,n)std::cin>>a[i]
#define rep(i,x,n) for(int i=x;i<=n;i++)
#define dep(i,x,n) for(int i=x;i>=n;i--)
#define erg(i,x) for(int i=head[x];i;i=e[i].nex)
#define dbg(x) std::cout<<#x<<":"<<x<<" "
#define mem(a,x) memset(a,x,sizeof a)
#define all(x) x.begin(),x.end()
#define arrall(a,n) a+1,a+1+n
#define PII std::pair<int,int>
#define m_p std::make_pair
#define u_b upper_bound
#define l_b lower_bound
#define p_b push_back
#define CD const double
#define CI const int
#define int long long
#define il inline
#define ss second
#define ff first
#define itn int
CI N=1e6+5;
int l,r,ans,cnt[N];
void init() {rep(i,2,r) {if(cnt[i]!=0) {continue;}for(int j=i;j<=r;j+=i) {if(cnt[j]>=0) {cnt[j]++;}}for(int j=i*i;j<=r;j+=i*i) {cnt[j]=-1;}}
}
signed main() {std::cin>>l>>r;init();rep(i,2,r) {if(cnt[i]<0) {continue;}int s=r/i-(l-1)/i;s=s*(s-1)/2;if(cnt[i]%2) {ans+=s;} else {ans-=s;}}rep(i,std::max(l,2ll),r) {ans-=r/i-1;}std::cout<<ans*2;return 0;
}