目录
1 主要内容
基础模型
2 部分代码
3 部分程序结果
4 下载链接
1 主要内容
该程序为文章《Two-Timescale Stochastic Dispatch of Smart Distribution Grids》的源代码,主要做的是主动配电网的双时间尺度随机优化调度,该模型考虑配电网的高效和安全运行涉及到在不同的时间尺度上的决策,如电压控制器可以在慢时间尺度进行调度,而光伏需要在快时间尺度调度和调节,以最佳地跟踪可再生能源发电和需求的变化,两种时间尺度通过耦合方式形成统一的优化调度模型。文中对于随机优化模型建立了两种方式,分别是平均调度算法和概率调度算法,这两种方法均基于辐射网络线性分布潮流(LDF)模型,模型涉及拉格朗日、非凸转换等深度内容,非常适合用来学习。程序采用matlab+cvx进行求解,程序采用模块化方式、采用英文注释,适合有编程经验的同学深度学习!

-
基础模型
该模型通过引入A建立配网潮流模型,通过电流流向(始端和终端)建立线路和节点关联关系。

以此为基础通过进一步推导和变量集合,形成优化调度模型。
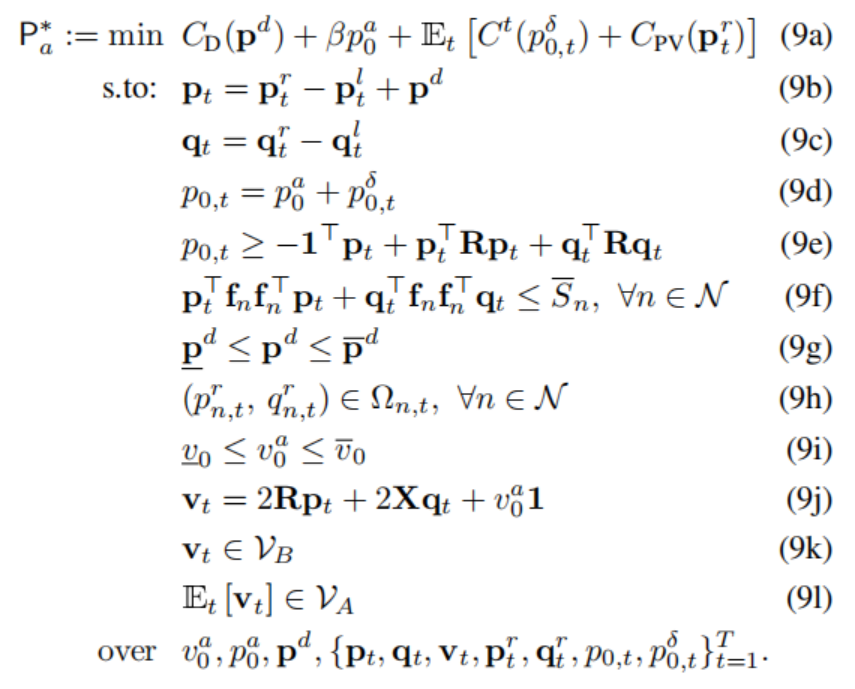
将上述模型中的(9l)替换为下述概率模型即可形成概率调度算法。

模型中目标函数涉及到在慢时间尺度上的能量调度成本加上快速时间尺度上的平均能源管理成本,(9b)-(9c)确保节点(无功)有功功率平衡,(9e)考虑有功功率损失,(9f)是线性潮流容量约束,(9i)-(9l)是电压约束,其中(9l)为平均电压约束,替换成(10)即形成概率电压约束。
2 部分代码
clear; close all
%%
preprocess;
%buses_pm = [3 5 14 25 32 51];
buses_pm = [];
b_pm = false(1, Nb);
b_pm(buses_pm) = 1;
buses_pd = [10, 18, 21, 30, 36, 43, 51, 55];
b_pd = false(1, Nb);
b_pd(buses_pd) = 1;
params = struct();
params.pm_lower = zeros(Nb, 1);
params.pm_upper = zeros(Nb, 1);
params.pm_upper(b_pm) = 0.25;
%http://www.powermag.com/microturbine-technology-matures/
microturbine_pf = 0.8;
params.pm_diag_phi = diag(b_pm)*tan(acos(microturbine_pf));
params.pm_linear = 40*ones(Nb,1); % reasonable value
params.pm_quadratic = 20*ones(Nb,1); % to give some curvature
% pm_space = linspace(0, 0.2, 100);
% plot(pm_space, mean(params.pm_linear) * pm_space + ...
% mean(params.pm_quadratic) * pm_space.^2);
params.pd_lower = zeros(Nb, 1);
params.pd_upper = zeros(Nb, 1);
params.pd_upper(b_pd) = 0.5;
params.pd_linear = 30*ones(Nb, 1); %must be higher than solar% should be lower than the microturbines linear term
params.pd_quadratic = 15*ones(Nb, 1);
if(0),pd_space = linspace(0, 0.5, 100);plot(pd_space, mean(params.pd_linear) * pd_space + ...mean(params.pd_quadratic) * pd_space.^2);
end
params.S2 = 7.^2*ones(Nb,1); % indirectly effects a limit on the substation injection
params.pi_inverter = 0.0*ones(Nb,1); % typical value (1/2 ret)
params.beta = 37;
params.gammaB = 45;
params.gammaS = 19;
%buses_pv = [15 22 31 40 44 50];
%buses_pv = 44;
buses_pv = [44 50];
b_pv = zeros(Nb,1);
b_pv(buses_pv) = 1;
%nominal_pv = 2*b_pv; % smaller PV systems than in SCE model
nominal_pv = 5*b_pv; %SCE 56 nodes (Gan, Li, Topcu and Low)
params.s2_inverter = (1.2*nominal_pv).^2;
inverter_pf = 0.85; % Dall'Anese, Dhople, and Giannakis, 2014
params.phi_inverter = b_pv*tan(acos(inverter_pf));
params.alpha = 0.05;
%%
v_bounds_tight = struct();
v_bounds_tight.v_upper = 1.02.^2*ones(Nb, 1);
v_bounds_tight.v_lower = 0.98.^2*ones(Nb, 1);
v_bounds_loose = struct();
v_bounds_loose.v_upper = 1.03.^2*ones(Nb, 1);
v_bounds_loose.v_lower = 0.97.^2*ones(Nb, 1);
v0_bounds = struct();
v0_bounds.v_upper = 1.03.^2;
v0_bounds.v_lower = 0.97.^2;
%%
load_max_pf = 0.85; load_phi = tan(acos(load_max_pf));
tnomi_p_load = 1; %how many times the nominal load is the mean
stdev_p_load = 0.2; %standard deviation of the random var
stdev_q_load = load_phi*(tnomi_p_load/3 - stdev_p_load);
% This line adjusts the reactive load's stdev_q considering that
% the "worst-case" power factor takes place when
% the active load is 3*stdev_p below the mean and reactive load
% is 3*stdev_q in absolute value.
prop_p_avail = 0.5; %proportion of the available p that is
% randomized via a uniform distribution.
n_rlz = 500; % number of realizations of the random vars
hyp.seed = 20;
rng(hyp.seed);
random_vars = struct();
random_vars.p_load = ...tnomi_p_load*nominal_loads(2:end)*ones(1, n_rlz) ...+ stdev_p_load*diag(nominal_loads(2:end))*randn(Nb, n_rlz);
random_vars.q_load = ...stdev_q_load*diag(nominal_loads(2:end))*randn(Nb, n_rlz);
random_vars.pinv_available = ...diag(nominal_pv)*(1-prop_p_avail*rand(Nb, n_rlz));
random_vars_mean = struct();
random_vars_mean.p_load = tnomi_p_load*nominal_loads(2:end);
random_vars_mean.q_load = 0*nominal_loads(2:end);
random_vars_mean.pinv_available = (1-prop_p_avail/2)*nominal_pv;
first_stage_initial = solve_average (benchmark, params, ...random_vars_mean, v_bounds_tight);
%nu_initial = 0.2;
%%
hyp.n_iterations = n_rlz;
hyp.epsilon0_p0 = 4/50/5;
hyp.epsilon0_v0 = 0.02/50;
hyp.epsilon0_pd = 0.3/50;
hyp.mu0 = 1.5*50*3;
hyp.evaluate_output = 0;
%hyp.stepsize_mode = 'constant';
hyp.stepsize_mode = 'O(1/sqrt(k))';
hyp.precision = 'low';
hyp.r = 0.5;
nu_upper_initial = zeros(Nb, 1); nu_upper_initial(1) = 0; %0.8;
nu_lower_initial = zeros(Nb, 1); nu_lower_initial(36) = 0; %0.6;
results = stochastic_solver_avg(benchmark, ...first_stage_initial, nu_lower_initial, nu_upper_initial, ...random_vars, params, ...v_bounds_tight, v_bounds_loose, v0_bounds, hyp, ...struct('plot', 1));
%%
filename = ['run-' datestr(now)];
filename(16)='_';
filename(filename==':') = [];
save(filename)
display(['Saved ' filename]);
beep
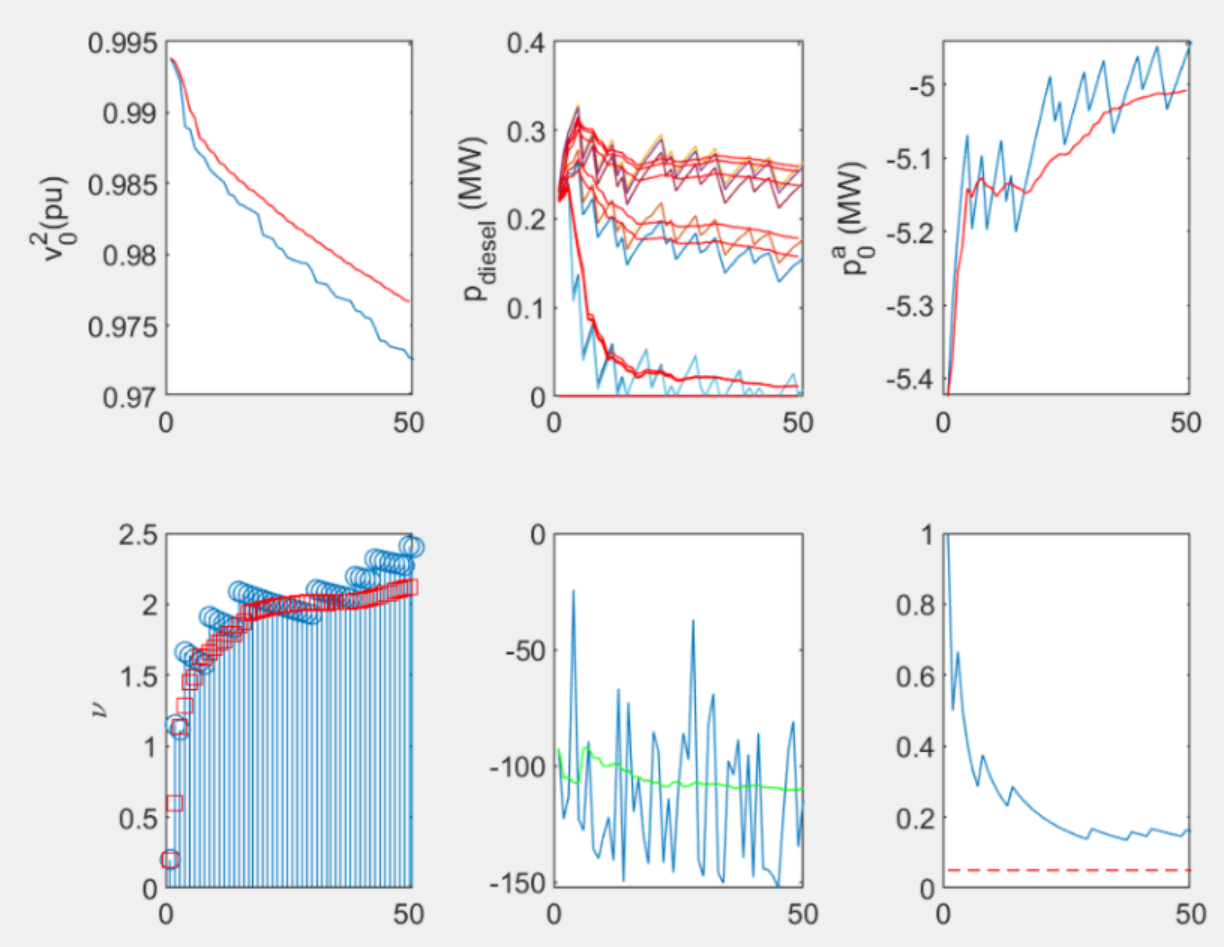
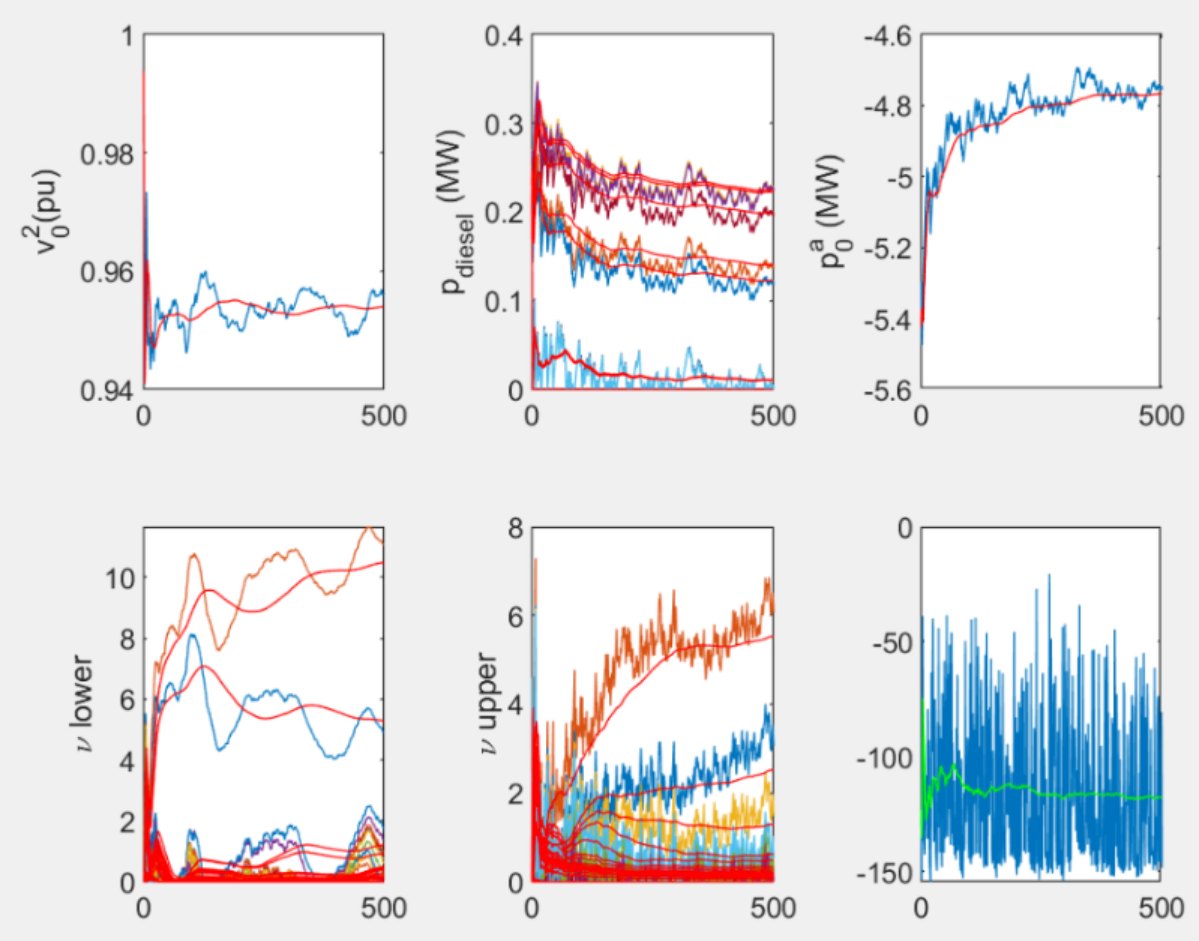
3 部分程序结果