文章目录
- 其他经典例题跳转链接
- 41.基数排序法
- 42.循序搜寻法(使用卫兵)
- 43.二分搜寻法(搜寻原则的代表)
- 44.插补搜寻法
- 45.费氏搜寻法
其他经典例题跳转链接
C语言经典算法-1
1.汉若塔 2. 费式数列 3. 巴斯卡三角形 4. 三色棋 5. 老鼠走迷官(一)6. 老鼠走迷官(二)7. 骑士走棋盘8. 八皇后9. 八枚银币10. 生命游戏
C语言经典算法-2
字串核对、双色、三色河内塔、背包问题(Knapsack Problem)、蒙地卡罗法求 PI、Eratosthenes筛选求质数
C语言经典算法-3
超长整数运算(大数运算)、长 PI、最大公因数、最小公倍数、因式分解、完美数、阿姆斯壮数
C语言经典算法-4
最大访客数、中序式转后序式(前序式)、后序式的运算、洗扑克牌(乱数排列)、Craps赌博游戏
C语言经典算法-5
约瑟夫问题(Josephus Problem)、排列组合、格雷码(Gray Code)、产生可能的集合、m元素集合的n个元素子集
C语言经典算法-6
数字拆解、得分排行,选择、插入、气泡排序、Shell 排序法 - 改良的插入排序、Shaker 排序法 - 改良的气泡排序
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-8
基数排序法、循序搜寻法(使用卫兵)、二分搜寻法(搜寻原则的代表)、插补搜寻法、费氏搜寻法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵
41.基数排序法
说明在之前所介绍过的排序方法,都是属于「比较性」的排序法,也就是每次排序时 ,都是比较整个键值的大小以进行排序。
这边所要介绍的「基数排序法」(radix sort)则是属于「分配式排序」(distribution sort),基数排序法又称「桶子法」(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些「桶」中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog®m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的比较性排序法。
解法基数排序的方式可以采用LSD(Least sgnificant digital)或MSD(Most sgnificant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
以LSD为例,假设原来有一串数值如下所示:
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
首先根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中:

接下来将这些桶子中的数值重新串接起来,成为以下的数列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着再进行一次分配,这次是根据十位数来分配:

接下来将这些桶子中的数值重新串接起来,成为以下的数列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
这时候整个数列已经排序完毕;如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好,MSD的方式恰与LSD相反,是由高位数为基底开始进行分配,其他的演 算方式则都相同。
#include <stdio.h>
#include <stdlib.h> int main(void) { int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81}; int temp[10][10] = {0}; int order[10] = {0}; int i, j, k, n, lsd; k = 0; n = 1; printf("\n排序前: "); for(i = 0; i < 10; i++) printf("%d ", data[i]); putchar('\n'); while(n <= 10) { for(i = 0; i < 10; i++) { lsd = ((data[i] / n) % 10); temp[lsd][order[lsd]] = data[i]; order[lsd]++; } printf("\n重新排列: "); for(i = 0; i < 10; i++) { if(order[i] != 0) for(j = 0; j < order[i]; j++) { data[k] = temp[i][j]; printf("%d ", data[k]); k++; } order[i] = 0; } n *= 10; k = 0; } putchar('\n'); printf("\n排序后: "); for(i = 0; i < 10; i++) printf("%d ", data[i]); return 0;
}
42.循序搜寻法(使用卫兵)
说明
搜寻的目的,是在「已排序的资料」中寻找指定的资料,而当中循序搜寻是最基本的搜寻法,只要从资料开头寻找到最后,看看是否找到资料即可。
解法
初学者看到循序搜寻,多数都会使用以下的方式来进行搜寻:
while(i < MAX) { if(number[i] == k) { printf("找到指定值"); break; } i++;
}
这个方法基本上没有错,但是可以加以改善,可以利用设定卫兵的方式,省去if判断式,卫兵通常设定在数列最后或是最前方,假设设定在列前方好了(索引0的 位置),我们从数列后方向前找,如果找到指定的资料时,其索引值不是0,表示在数列走访完之前就找到了,在程式的撰写上,只要使用一个while回圈就可 以了。
下面的程式为了配合卫兵的设置,自行使用快速排序法先将产生的数列排序,然后才进行搜寻,若只是数字的话,通常您可以使用程式语言函式库所提供的搜寻函式。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} int search(int[]);
int partition(int[], int, int);
void quicksort(int[], int, int); int main(void) { int number[MAX+1] = {0}; int i, find; srand(time(NULL)); for(i = 1; i <= MAX; i++) number[i] = rand() % 100; quicksort(number, 1, MAX); printf("数列:"); for(i = 1; i <= MAX; i++) printf("%d ", number[i]); printf("\n输入搜寻值:"); scanf("%d", &number[0]); if(find = search(number)) printf("\n找到数值于索引 %d ", find); else printf("\n找不到数值"); printf("\n"); return 0;
} int search(int number[]) { int i, k; k = number[0]; i = MAX; while(number[i] != k) i--; return i;
} int partition(int number[], int left, int right) { int i, j, s; s = number[right]; i = left - 1; for(j = left; j < right; j++) { if(number[j] <= s) { i++; SWAP(number[i], number[j]); } } SWAP(number[i+1], number[right]); return i+1;
} void quicksort(int number[], int left, int right) { int q; if(left < right) { q = partition(number, left, right); quicksort(number, left, q-1); quicksort(number, q+1, right); }
}
43.二分搜寻法(搜寻原则的代表)
说明如果搜寻的数列已经有排序,应该尽量利用它们已排序的特性,以减少搜寻比对的次数,这是搜寻的基本原则,二分搜寻法是这个基本原则的代表。
解法在二分搜寻法中,从数列的中间开始搜寻,如果这个数小于我们所搜寻的数,由于数列已排序,则该数左边的数一定都小于要搜寻的对象,所以无需浪费时间在左边的数;如果搜寻的数大于所搜寻的对象,则右边的数无需再搜寻,直接搜寻左边的数。
所以在二分搜寻法中,将数列不断的分为两个部份,每次从分割的部份中取中间数比对,例如要搜寻92于以下的数列,首先中间数索引为(0+9)/2 = 4(索引由0开始):
[3 24 57 57 67 68 83 90 92 95]
由于67小于92,所以转搜寻右边的数列:
3 24 57 57 67 [68 83 90 92 95]
由于90小于92,再搜寻右边的数列,这次就找到所要的数了:
3 24 57 57 67 68 83 90 [92 95]
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void quicksort(int[], int, int);
int bisearch(int[], int); int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; } quicksort(number, 0, MAX-1); printf("数列:"); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = bisearch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} int bisearch(int number[], int find) { int low, mid, upper; low = 0; upper = MAX - 1; while(low <= upper) { mid = (low+upper) / 2; if(number[mid] < find) low = mid+1; else if(number[mid] > find) upper = mid - 1; else return mid; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
44.插补搜寻法
说明
如果却搜寻的资料分布平均的话,可以使用插补(Interpolation)搜寻法来进行搜寻,在搜寻的对象大于500时,插补搜寻法会比 二分搜寻法 来的快速。
解法
插补搜寻法是以资料分布的近似直线来作比例运算,以求出中间的索引并进行资料比对,如果取出的值小于要寻找的值,则提高下界,如果取出的值大于要寻找的 值,则降低下界,如此不断的减少搜寻的范围,所以其本原则与二分搜寻法是相同的,至于中间值的寻找是透过比例运算,如下所示,其中K是指定要寻找的对象, 而m则是可能的索引值:
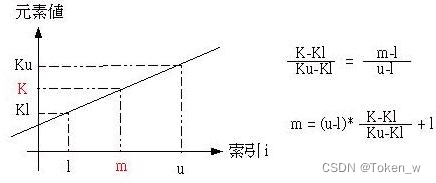
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 10
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void quicksort(int[], int, int);
int intsrch(int[], int); int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 0; i < MAX; i++) { number[i] = rand() % 100; } quicksort(number, 0, MAX-1); printf("数列:"); for(i = 0; i < MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = intsrch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} int intsrch(int number[], int find) { int low, mid, upper; low = 0; upper = MAX - 1; while(low <= upper) { mid = (upper-low)* (find-number[low])/(number[upper]-number[low]) + low; if(mid < low || mid > upper) return -1; if(find < number[mid]) upper = mid - 1; else if(find > number[mid]) low = mid + 1; else return mid; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
45.费氏搜寻法
说明
二分搜寻法每次搜寻时,都会将搜寻区间分为一半,所以其搜寻时间为O(log(2)n),log(2)表示以2为底的log值,这边要介绍的费氏搜寻,其利用费氏数列作为间隔来搜寻下一个数,所以区间收敛的速度更快,搜寻时间为O(logn)。
解法
费氏搜寻使用费氏数列来决定下一个数的搜寻位置,所以必须先制作费氏数列,这在之前有提过;费氏搜寻会先透过公式计算求出第一个要搜寻数的位置,以及其代 表的费氏数,以搜寻对象10个数字来说,第一个费氏数经计算后一定是F5,而第一个要搜寻的位置有两个可能,例如若在下面的数列搜寻的话(为了计算方便, 通常会将索引0订作无限小的数,而数列由索引1开始):
-infin; 1 3 5 7 9 13 15 17 19 20
如果要搜寻5的话,则由索引F5 = 5开始搜寻,接下来如果数列中的数小于指定搜寻值时,就往左找,大于时就向右,每次找的间隔是F4、F3、F2来寻找,当费氏数为0时还没找到,就表示寻找失败,如下所示:
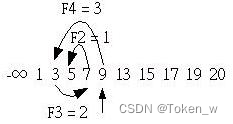
由于第一个搜寻值索引F5 = 5处的值小于19,所以此时必须对齐数列右方,也就是将第一个搜寻值的索引改为F5+2 = 7,然后如同上述的方式进行搜寻,如下所示:
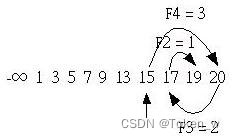
至于第一个搜寻值是如何找到的?我们可以由以下这个公式来求得,其中n为搜寻对象的个数:
Fx + m = n
Fx <= n
也就是说Fx必须找到不大于n的费氏数,以10个搜寻对象来说:
Fx + m = 10
取Fx = 8, m = 2,所以我们可以对照费氏数列得x = 6,然而第一个数的可能位置之一并不是F6,而是第x-1的费氏数,也就是F5 = 5。
如果数列number在索引5处的值小于指定的搜寻值,则第一个搜寻位置就是索引5的位置,如果大于指定的搜寻值,则第一个搜寻位置必须加上m,也就是F5 + m = 5 + 2 = 7,也就是索引7的位置,其实加上m的原因,是为了要让下一个搜寻值刚好是数列的最后一个位置。
费氏搜寻看来难懂,但只要掌握Fx + m = n这个公式,自己找几个实例算一次,很容易就可以理解;费氏搜寻除了收敛快速之外,由于其本身只会使用到加法与减法,在运算上也可以加快。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 15
#define SWAP(x,y) {int t; t = x; x = y; y = t;} void createfib(void); // 建立费氏数列
int findx(int, int); // 找x值
int fibsearch(int[], int); // 费氏搜寻
void quicksort(int[], int, int); // 快速排序 int Fib[MAX] = {-999}; int main(void) { int number[MAX] = {0}; int i, find; srand(time(NULL)); for(i = 1; i <= MAX; i++) { number[i] = rand() % 100; } quicksort(number, 1, MAX); printf("数列:"); for(i = 1; i <= MAX; i++) printf("%d ", number[i]); printf("\n输入寻找对象:"); scanf("%d", &find); if((i = fibsearch(number, find)) >= 0) printf("找到数字于索引 %d ", i); else printf("\n找不到指定数"); printf("\n"); return 0;
} // 建立费氏数列
void createfib(void) { int i; Fib[0] = 0; Fib[1] = 1; for(i = 2; i < MAX; i++) Fib[i] = Fib[i-1] + Fib[i-2];
} // 找 x 值
int findx(int n, int find) { int i = 0; while(Fib[i] <= n) i++; i--; return i;
} // 费式搜寻
int fibsearch(int number[], int find) { int i, x, m; createfib(); x = findx(MAX+1,find); m = MAX - Fib[x]; printf("\nx = %d, m = %d, Fib[x] = %d\n\n", x, m, Fib[x]); x--; i = x; if(number[i] < find) i += m; while(Fib[x] > 0) { if(number[i] < find) i += Fib[--x]; else if(number[i] > find) i -= Fib[--x]; else return i; } return -1;
} void quicksort(int number[], int left, int right) { int i, j, k, s; if(left < right) { s = number[(left+right)/2]; i = left - 1; j = right + 1; while(1) { while(number[++i] < s) ; // 向右找 while(number[--j] > s) ; // 向左找 if(i >= j) break; SWAP(number[i], number[j]); } quicksort(number, left, i-1); // 对左边进行递回 quicksort(number, j+1, right); // 对右边进行递回 }
}
系列好文,点击链接即可跳转
C语言经典算法-7
排序法 - 改良的选择排序、快速排序法(一)、快速排序法(二)、快速排序法(三)、合并排序法
C语言经典算法-9
稀疏矩阵、多维矩阵转一维矩阵、上三角、下三角、对称矩阵、奇数魔方阵、4N 魔方阵、2(2N+1) 魔方阵