NURBS曲线,全称非均匀有理B样条曲线(Non-Uniform Rational B-Splines),是计算机图形学中用于表示几何形状的数学表示方法。它结合了非均匀B样条(B-Splines)和有理基函数(Rational Basis Functions)的特性,从而能够更精确地描述和表示复杂的几何形状。
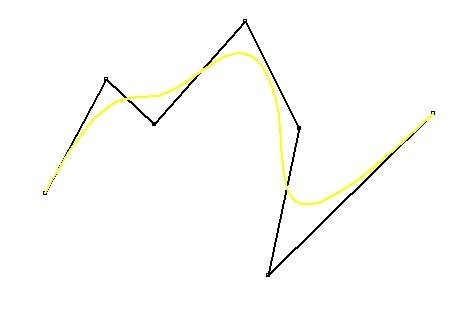
NURBS曲线的主要特点包括:
非均匀性:NURBS曲线的节点向量(knot vector)的值和间距可以是任意的,这使得在不同区间上可以得到不同的混合函数形状,为自由控制曲线形状提供了更大的灵活性。
有理性:通过引入权因子(weight factor),NURBS曲线能够更精确地表示曲线上的点,特别是在处理圆锥曲线和圆等复杂形状时具有优势。
局部性:NURBS曲线的修改只影响与其相关的部分,对曲线的其他部分没有影响,这使得曲线编辑更加高效和直观。
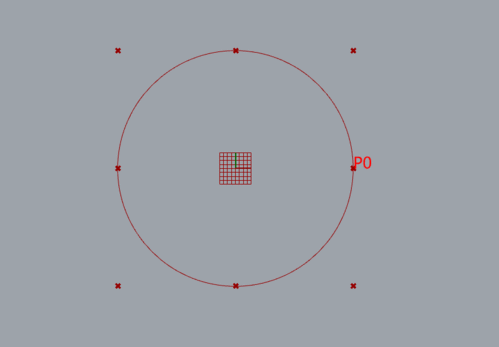
将圆转换为NURBS曲线涉及到用NURBS的表示方法近似地表示一个圆的几何形状。NURBS曲线通常用于表示更复杂的形状,但也可以用来近似简单的形状,如圆。以下是转换圆为NURBS曲线的实例:
#include "gp_Circ2d.hxx"
#include "Convert_ParameterisationType.hxx"
#include "Convert_CircleToBSplineCurve.hxx"
#include "GC_MakeCircle.hxx"
#include "GeomConvert.hxx"
void DumpConvertorInfo(const Convert_CircleToBSplineCurve& theConvertor)
{Standard_Integer aCounter = 0;std::cout << "Convert Result" << std::endl;std::cout << "Degree: " << theConvertor.Degree() << std::endl;std::cout << "Periodic: " << (theConvertor.IsPeriodic() ? "yes" : "no") << std::endl;std::cout << "Knots: " << std::endl;for (Standard_Integer i = 1; i <= theConvertor.NbKnots(); ++i){for (Standard_Integer j = 1; j <= theConvertor.Multiplicity(i); ++j){std::cout << ++aCounter << ": " << theConvertor.Knot(i) << std::endl;}}std::cout << "Poles(Weight): " << std::endl;for (Standard_Integer i = 1; i <= theConvertor.NbPoles(); ++i){gp_Pnt2d aPole = theConvertor.Pole(i);std::cout << i << ": " << aPole.X() << ", " << aPole.Y()<< " W(" << theConvertor.Weight(i) << ")" << std::endl;}
}
int main() {gp_Circ2d aCircle;aCircle.SetRadius(1.0);Convert_ParameterisationType aType = Convert_TgtThetaOver2;Convert_CircleToBSplineCurve aConvertor(aCircle, aType);
Handle(Geom_Circle) aGeomCircle = GC_MakeCircle(gp::XOY(), 1.0);Handle(Geom_BSplineCurve) aBSplineCurve = GeomConvert::CurveToBSplineCurve(aGeomCircle, aType);
std::cout << "Convert Circle to BSpline Curve: " << std::endl;DumpConvertorInfo(aConvertor);
return 0;
}Convert Circle to BSpline Curve:
Convert Result
Degree: 2
Periodic: yes
Knots:
1: 0
2: 0
3: 2.0944
4: 2.0944
5: 4.18879
6: 4.18879
7: 6.28319
8: 6.28319
Poles(Weight):
1: 1, 0 W(1)
2: 1, 1.73205 W(0.5)
3: -0.5, 0.866025 W(1)
4: -2, 2.44929e-16 W(0.5)
5: -0.5, -0.866025 W(1)
6: 1, -1.73205 W(0.5)
![[leetcode] 240. 搜索二维矩阵 II](https://img-blog.csdnimg.cn/direct/a5a6570d40564dc3b6873b84f3a7ab62.png)