上一篇文章中，我们了解了Boosting思想的两种算法：Adboost和GBDT；其中对于GBDT算法，存在两种改进，即：

• XGBoost
• LightGBM

一. XGBoost 算法

XGBoost是GBDT(梯度提升树)的一个改进版本
    能够更快的、更高效率的训练模型
    X代表的就是eXtreme（极致）

	学习器：决策树将这些决策树称为”弱学习器“，这些”弱学习器“共同组成了XGboost算法思想：XGBoost的决策树之间是有先后顺序后一棵决策树的生成会考虑前一棵决策树的预测结果，即：将前一棵决策树的偏差考虑在内，也就是更改y值数据使用：生成每棵决策树使用的是整个数据集

1. XGBoost 算法流程

1. 构造初始化常数函数，以及模型跟新
   $F_0(x)=f_0(x)=0$

   $F_1(x)=F_0(x)+f_1(x)$

   $F_2(x)=F_1(x)+f_2(x)$

   $......$

   $F_0(x)=F_{(k-1)}(x)+f_k(x)$

   我们的目标为：求出函数$f_1(x)$，$f_2(x)$，…，$f_k(x)$

2. 定义损失函数
   XGBoost算法的损失函数：在GBDT的基础上增加了正则化项，用于限制模型的复杂度
   $$obj=\sum _{i=1}^{n}L\left(y_i,F_i^{(k)}(x)\right)+\sum _{i=1}^k\Omega \left(f_i\right)$$

   公式解释：
    
   $obj函数$ 为构建$k$棵树的总损失

   预测误差 + 每棵树复杂度的惩罚项

   对于正则化项，我们做出以下公式优化：
   $$f_k(x)=w_{q(x)}$$
   $$\Omega (f)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$

   公式解释：
   $f_k(x)$可以表示一棵树

   f 是一棵决策树，$f_k$是第$k$棵决策树
   x 是一个样本，丢进$f函数$中就需要对该样本进行预测
   $q(x)$ 表示进入的样本x落在哪个叶子节点中
   $w_{q(x)}$ 是叶子节点$q(x)$的值

   先算在哪个叶子节点上，然后根据该叶子节点的值返回

   $\Omega (f)$可以表示一棵树的复杂程度

   T 表示这棵决策树叶子节点的数量：叶子节点越多，决策树越复杂
   $w_j^2$ 表示所有叶子节点值的平方和

   $w$为叶子节点的值
   由于每个弱学习器拟合的都是残差，所以$w$不能太大
   如果模型企图去拟合离群点，那么$w$就会变大

   此时，目标函数可以写为
   $$L^k=\sum _{i=1}^{n}L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]+\sum _{j=1}^K\Omega \left(f_j\right)$$

   公式推导：
    
   $L^k$
    
   $={\sum }_{i=1}^{n}L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]+{\sum }_{j=1}^K\Omega \left(f_j\right)$
    
   $={\sum }_{i=1}^{n}L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]+{\sum }_{j=1}^{k-1}\Omega \left(f_j\right)+\Omega \left(f_k\right)$
    
   $={\sum }_{i=1}^{n}L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]+\Omega \left(f_k\right)$

即：$$L^k=\sum _{i=1}^{n}L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]+\Omega \left(f_k\right)$$
3. 二阶展开
 
一元函数在x0点的泰勒展式：
$$f(x)=f\left(x_0\right)+f^{\prime }\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\dots +\frac{f^{(n)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n+\dots$$
注意：我们只求至二阶导即可
所以，对于$L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]$，可以写为：

$L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]$

$=L[y_i,F_{k-1}(x)]+{\partial }_{F_{k-1}}L[y_i,F_{k-1}(x)]f_k\left(x_i\right)+\frac{1}{2}{\partial }_{F_{k-1}}^{2}L[y_i,F_{k-1}(x)]f_k^2\left(x_i\right)$

其中：
$$g_i={\partial }_{F_{k-1}}L[y_i,F_{k-1}(x)]，即L关于x_0的一阶导$$
$$h_i={\partial }_{F_{k-1}}^{2}L[y_i,F_{k-1}(x)]，即L关于x_0的二阶导$$

对于$L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]$

$x=F_{k-1}(x)+f_k\left(x_i\right)$
 
$x_0=F_{k-1}(x)$
 
$x-x_0=f_k(x_i)$

i为样本，所以$g_i，h_i$是可以计算得到的
也就是说，$L[y_i,F_{k-1}(x)]$为常数

即，为了求下一棵树，我需要求每个样本的一阶导，二阶导

因此，我们可以得到：
$$L\left[y_i,F_{k-1}(x)+f_k\left(x_i\right)\right]=L[y_i,F_{k-1}(x)]+g_i\ast f_k\left(x_i\right)+\frac{1}{2}{h}_i\ast f_k^2\left(x_i\right)$$
因为$L[y_i,F_{k-1}(x)]$为常数，所以对于每个样本，可以得到：
$$L^k=\sum _{i=1}^n{g}_i\ast f_k\left(x_i\right)+\frac{1}{2}{h}_i\ast f_k^2\left(x_i\right)$$
$$L^k=\sum _{i=1}^n\left(g_i\ast w_{q\left(x_i\right)}+\frac{1}{2}{h}_i\ast w_{q\left(x_i\right)}^2\right)+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$

我们认为，对于n个样本，最终会落到T个叶子节点上去
也就是说，对于某一个叶子节点：

$g_a+g_b+g_c+....=G_j$

同理，也可得到$H_j$

将公式转换为对于每个每个叶子节点求和，我们就可以得到：
$$L^k=\sum _{j=1}^T\left(G_j\ast w_j+\frac{1}{2}{H}_j\ast w_j^2\right)+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
合并后，最终得到的损失函数为：
$$L^k=\sum _{j=1}^T\left(G_j\ast w_j+\frac{1}{2}\left(H_j+\lambda \right)\ast w_j^2\right)+\gamma T$$

4. 为了使损失函数最小，需要损失函数对于$w_j$ 求导，并令导数为0，求得最优的w：

    	注意：此时树的结构是确定的，即q函数确定
   

$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$$
即：每个叶子节点值为$w_j^{\ast }$时，模型最佳

将$w$带入，得到最小损失为：
$$L_{\min }^k=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

5. 计算增益

上面，我们在树结构确定时，算出来最小损失
那么，我们现在的问题是：怎么确定树的结构？

对于一次节点分裂，显然损失下降越多，分裂节点越佳

这里我们解释${\sum }_{j=1}^T{G}_j$：
假设数据集中共存在10个样本：$g_1，g_2，...，g_{10}$

将样本1-5落在R叶子节点内
将样本6-10落在L叶子节点内

因此我们可以得到${\sum }_{j=1}^T{G}_j=G_R+G_L$
同理，可以得到$H_R，H_L$

对于分裂前，我们有：
$${\text{ loss }}_{\text{before }}=-\frac{1}{2}\frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }+\gamma$$
对于分裂后，我们有：
$${\text{ loss }}_{after}=-[\frac{1}{2}\frac{G_L^2}{H_L+\lambda }+\gamma ]-[\frac{1}{2}\frac{G_R^2}{H_R+\lambda }+\gamma ]=-\frac{1}{2}\left(\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }\right)+2\gamma$$

因此，信息增益为：

计算所有候选分裂点对应的gain
选择gain最大的分裂点进行分裂
如果一个节点的所有候选分裂点都不能带来gain，则该节点不分裂

$$gain=\frac{1}{2}\left(\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{{\left(G_L+G_R\right)}^2}{\left(H_L+H_R\right)+\lambda }\right)-\gamma$$

2. XGBoost 算法评价

• 与决策树不同，XGBoost并不直接使用基尼系数或信息增益这些指标来进行特征选择或分裂点选择，而是计算每个特征的分裂增益(Gain)来选择最佳的最佳的特征和分裂点，从而构建更准确的树模型
• 分裂增益表示在分裂前后损失函数的减少程度

在计算分裂增益时，有两种方式：

1. 精确算法：遍历所有特征的所有可能的分裂点，计算gain值，选择最大的 gain值对应的分裂点进行分裂
   如：上述公式推导部分

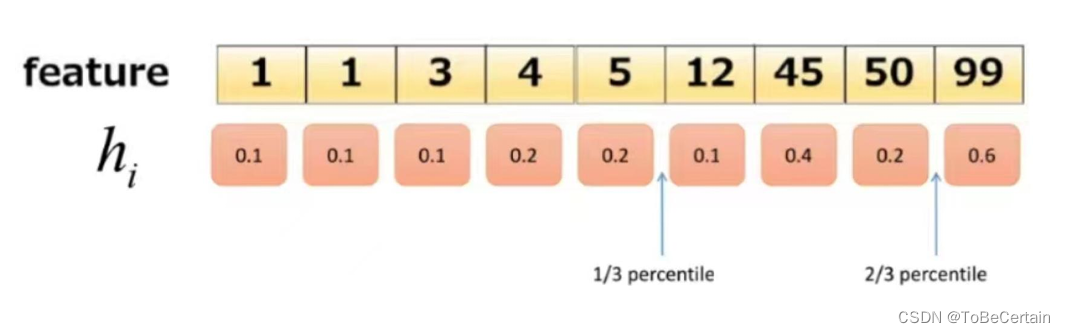
2. 近似算法：对于每个特征，只考虑分位点，减少计算复杂度

   	分位点：按照上一轮的预测误差函数的二阶导数值作为权重进行划分
   

二. LightGBM 算法

LightGBM是由微软开发的boosting集成模型，类似于XGBoost，对GBDT进行了优化和高效实现，原理有一些相似之处；但它的主要优势在于能够处理大规模数据

	在实验中：LightGBM 比 XGBoost 快将近10倍内存占用率大约为XGBoost的1/6

2. LightGBM 算法优势

	GBDT 在每一次迭代的时候，都需要遍历整个训练数据多次如果把整个训练数据一次性装进内存，会明显限制训练数据的大小如果不装进内存，反复地读写训练数据又会消耗非常大的时间。

面对大规模工业级数据，传统的GBDT算法无法满足需求。LightGBM的主要目的之一是解决上述大数据量级下的GBDT训练问题，以便在工业实践中支持大规模数据并保证效率

	算法思想：LightGBM提出直方图算法：为了减少分裂点的数量

直方图就是把连续的浮点特征离散化为k个整数(也就是分桶bins的思想)，比如：

$[0,0.1]=>0$
$[0.1,0.3]=>1$

这里的思想类似XGBoost的分位点

---

感谢阅读🌼
如果喜欢这篇文章，记得点赞👍和转发🔄哦！
有任何想法或问题，欢迎留言交流💬，我们下次见！
本文相关代码存放位置
    【Boosting思想 扩展算法 代码实现】

祝愉快🌟！

---