1.单值二叉树
965. 单值二叉树 - 力扣(LeetCode)
建立一个新的函数,用函数传参的方法来记录val的值
如上一篇最后的对称二叉树的习题,建立新的函数来传参

多采用使用反对值的方法,因为如果是相等return true的话,没有实质性的作用
bool _isUnivalTree(struct TreeNode* root,const int val){if(root==NULL){return true;}if(root->val!=val){return false;}return _isUnivalTree(root->left,val)&&_isUnivalTree(root->right,val);}
bool isUnivalTree(struct TreeNode* root) {if(root==NULL){return true;}int val=root->val;return _isUnivalTree(root,val);
}2.前序遍历
144. 二叉树的前序遍历 - 力扣(LeetCode)
力扣的统一要求,凡是返回数组,一定要返回数组大小

这样还能真的返回returnSize的大小吗?
经典的错误,标准的零分:传值调用!!
力扣是希望我们在函数内部修改好returnsize的值,这样他才能查看数组的大小以便于访问。
那我们怎么确定这个值大小呢?换句话问,我们如何开辟这个空间呢?
当然是不建议一次性开一个很大的数组来保证足够使用的。

我们可以模仿顺序表扩容的功能进行realloc,或者直接写一个计数节点个数的函数(此功能在上一篇中有讲)。

问题出在哪?
i成为一个局部变量,每次的值都不会改变。
我们任然需要采用传址调用的方法:
int TreeNodeSize(struct TreeNode* root){if(root==NULL){return 0;}return TreeNodeSize(root->left)+TreeNodeSize(root->right)+1;
}void _preorderPut(struct TreeNode* root,int* arr,int* pi){//前序遍历的顺序是根,左子树,右子树if(root==NULL){return;}arr[(*pi)++]=root->val;_preorderPut(root->left,arr,pi);_preorderPut(root->right,arr,pi);}int* preorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize=TreeNodeSize(root);int* arr=(int*)malloc(sizeof(int)*(*returnSize));//只创建一次数组即可,所以真正的遍历还是应当使用子函数int i=0;int* pi=&i;_preorderPut(root,arr,pi);return arr;
}3.判断是否为子树
572. 另一棵树的子树 - 力扣(LeetCode)
为空、树的比较是最小子问题,isSubtree(left or right)是递归子问题。
我们应该把这两个问题分开,不要将树的比较嵌套进递归中,而应该分隔开两个逻辑。此处树的比较非常类似于前面题目的:
root1->val==root2->val
只不过是将数值的比较换做了整个子树的比较,我们直接复用之前写好的比较树的函数即可
利用之前的函数:判断树是否相同。遍历主树,将主树的每个值与subroot相比较。

一如既往,在二叉树中空一直都是最小子问题,但是此处的空该return false还是return true呢?
根据题目描述,root不可能为空
满足一次return true就会一直在

每一次函数调用的“isSubtree”语句上做返回,层层返回,直到返回到函数外部
bool isSameTree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL && subRoot==NULL){return true;}if(root==NULL || subRoot==NULL){return false;}if(root->val!=subRoot->val){return false;}return isSameTree(root->left,subRoot->left)&&isSameTree(root->right,subRoot->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root==NULL){return false;}if(root->val==subRoot->val&&isSameTree(root,subRoot)){return true;}return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}4.二叉树的创建和销毁(非递归)
二叉树遍历_牛客题霸_牛客网 (nowcoder.com)
这个题完成创建
#include <stdio.h>
#include <stdlib.h>typedef struct BTNode {struct BTNode* left;struct BTNode* right;char val;
}BTNode;BTNode* CreatTree(char* arr, int* pi) {if (arr[*pi] == '#') {(*pi)++;return NULL;}BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->val = arr[(*pi)++];newnode->left = CreatTree(arr, pi);newnode->right = CreatTree(arr, pi);return newnode;
}void Inorder(BTNode* tree, char* arr) {//中序是左子树 根 右子树if (tree == NULL) {return;}Inorder(tree->left, arr);printf("%c ", tree->val);Inorder(tree->right, arr);
}int main() {char arr[100];scanf("%s", arr);int i = 0;BTNode* tree = CreatTree(arr, &i);Inorder(tree, arr);return 0;
}二叉树的销毁:
前序也能销毁,但是很麻烦,需要变量记录指针。
后序更佳:
后序+队列(利用队列的先进先出)
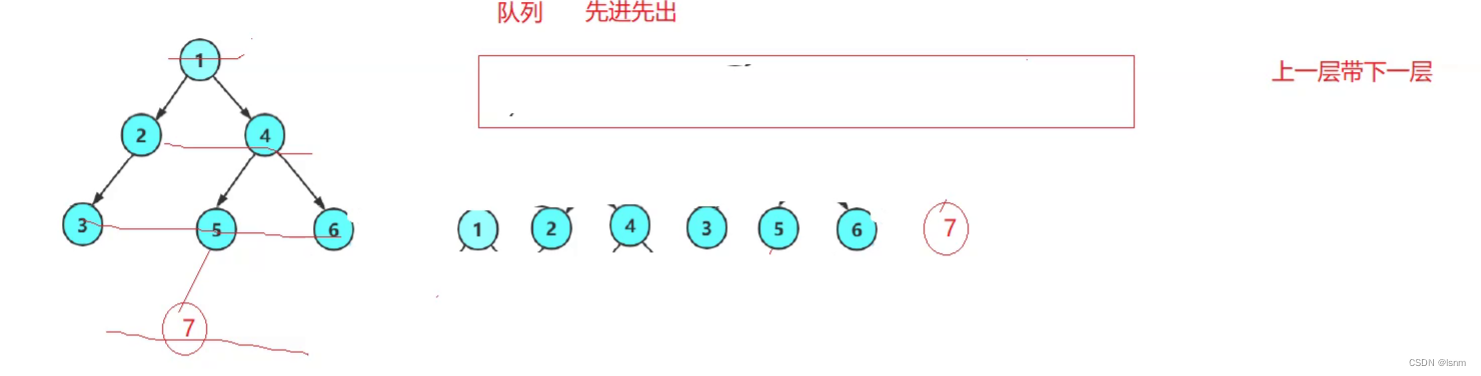
采取出来一个,带入自己的左右子节点
注意声明和定义的分离
将树节点指针当作队列节点的值放入队列中。