一种比较无脑暴力点的方法,时间复杂度是(n²+m)。
(注意==的优先级比^高,记得加括号(a[i]^a[j])==x)
#include <iostream>
#include <vector>
#include <bits/stdc++.h> // 包含一些 C++ 标准库中未包含的特定实现的函数的头文件
using namespace std;int main() {int n, m, x;// 输入 n(数组长度)、m(查询次数)、x(给定的异或值)cin >> n >> m >> x;// 定义数组 a 存储 n 个整数int a[n + 1];// 输入 n 个整数到数组 a 中for (int i = 1; i <= n; i++) {cin >> a[i];}// 定义动态规划数组 dp,初始化为 INT_MAX,记录a[i]第一次能异或为x的位置j。vector<int> dp(n + 1, INT_MAX);// 对于每对 i、j,判断 a[i] 和 a[j] 是否异或等于给定的 x// 如果等于,则更新 dp[i] 为 j,表示 a[i] 和 a[j] 可以异或得到 xfor (int i = 1; i < n; i++) {for (int j = i + 1; j <= n; j++) {if ((a[i] ^ a[j]) == x) {dp[i] = j;break; // 找到第一个符合条件的 j 即可跳出内层循环}}}// 对于每次查询,输入左右边界 l、r// 如果 l 不等于 r 并且 dp[l] 小于等于 r,则输出 "yes",否则输出 "no"for (int i = 0; i < m; i++) {int l, r;cin >> l >> r;if (l != r && dp[l] <= r)cout << "yes" << endl;elsecout << "no" << endl;}return 0;
}
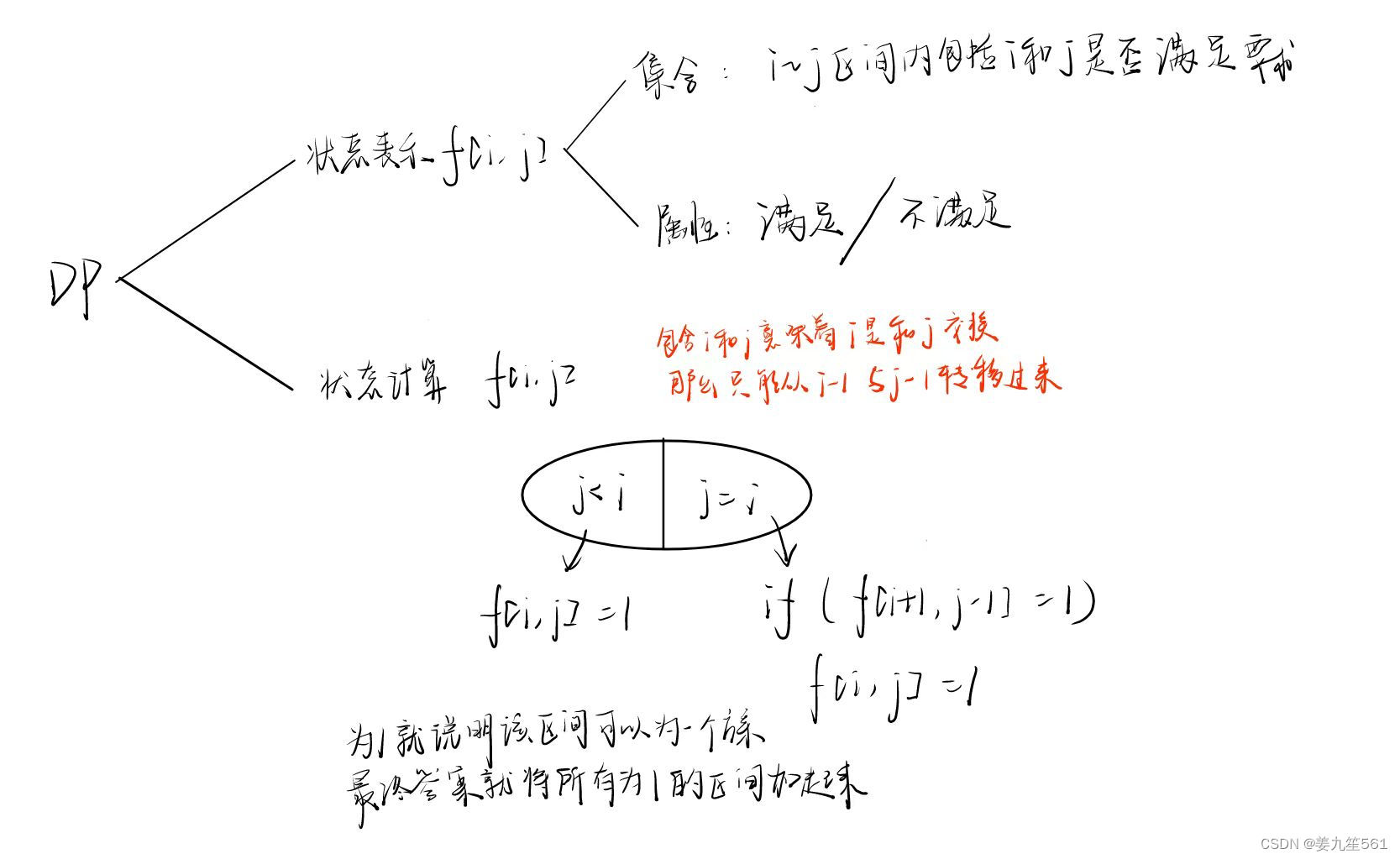
但是显然这样是不能得满分的,那么我们就要优化一下思路。
思路分析:
- 定义数组
a存储n个整数。 - 定义一个
map<int, int>,用于记录数组元素和它们的位置信息。(注意:map当某个键不存在时,其值会被初始为0) - 从标准输入流中读取
n个整数到数组a中。 - 定义动态规划数组
dp,初始化为 0,用于记录满足条件的[1,i]最远位置。 - 遍历数组
a,更新动态规划数组dp和map。 - 查询部分:从标准输入流中读取左右边界
l和r,判断是否存在满足条件的位置对,输出相应的结果。
#include<iostream>
#include<bits/stdc++.h>
using namespace std;int main() {int n, m, x;// 输入数组长度 n、查询次数 m 和给定的异或值 xcin >> n >> m >> x;// 定义数组 a 存储 n 个整数int a[n + 1];// 定义 map,用于记录数组元素和它们的位置信息map<int, int> map;// 输入 n 个整数到数组 a 中for(int i = 1; i <= n; i++) {cin >> a[i];}// 定义动态规划数组 dp,初始化为 0,用于记录满足条件的最远位置vector<int> dp(n + 1, 0);// 对数组 a 进行遍历for(int i = 1; i <= n; i++) {// 更新动态规划数组 dp// dp[i] 表示在位置 i 时,可以得到的满足条件的最远位置// 比较当前位置和之前出现的值对应位置的较大值,更新 dp[i]dp[i] = max(dp[i - 1], map[a[i] ^ x]);// 更新 map,记录当前元素的位置信息map[a[i]] = i;}// 查询部分for(int i = 0; i < m; i++) {int l, r;cin >> l >> r;// 如果左右边界不相等,并且 dp[r] 大于等于左边界 l,则输出 "yes",否则输出 "no"if(l != r && dp[r] >= l)cout << "yes" << endl;elsecout << "no" << endl;}return 0;
}
时间复杂度是O(n+m),大大优化了。