具体的设计方法 -- 黑盒测试
因果图
因果图是一种简化的逻辑图, 能直观地表明程序的输入条件(原因)和输出动作(结果)之间的相互关系. 因果图法是借助图形来设计测试用例的一种系统方法, 特别适用于被测试程序具有多种输入条件, 程序的输出又依赖于输入条件的各种情况.
因果图需要掌握的基本知识
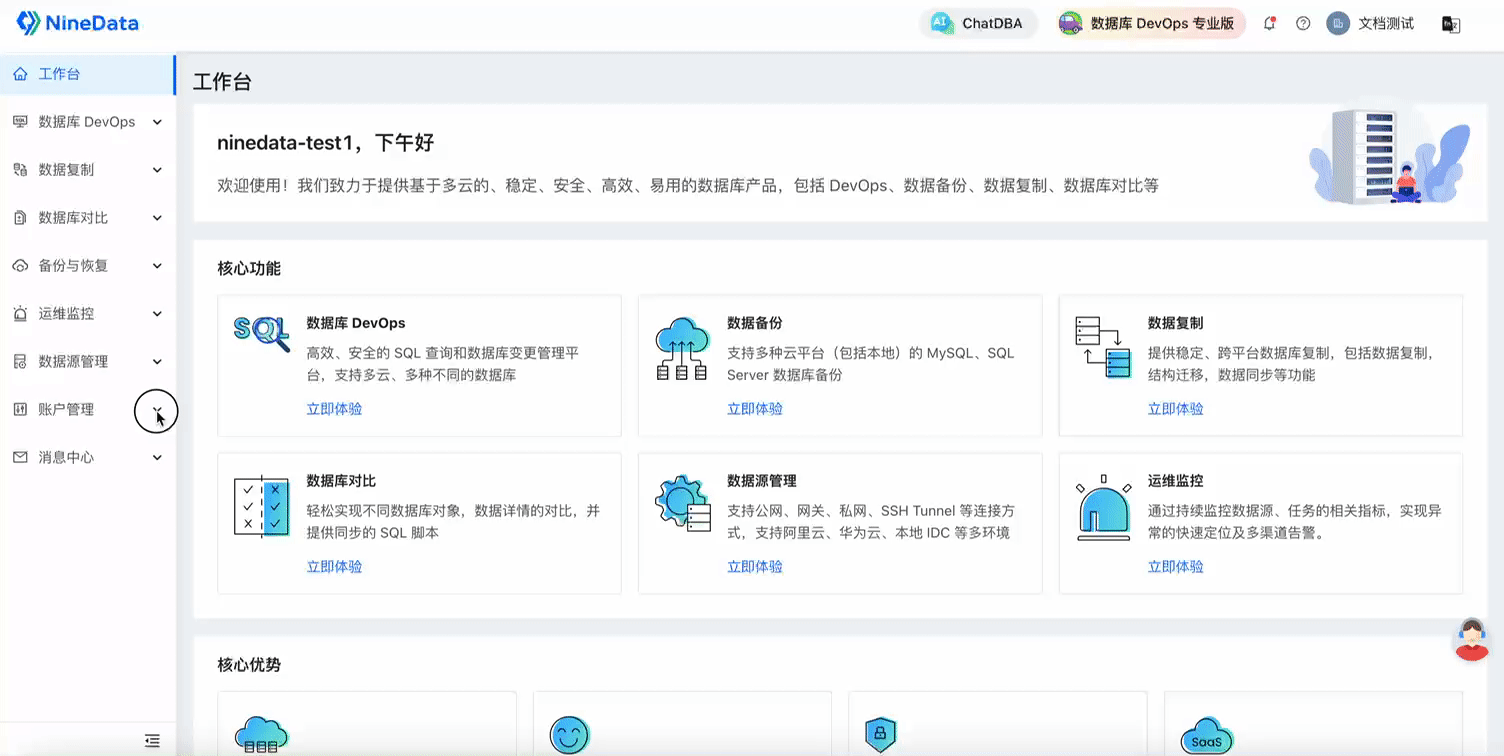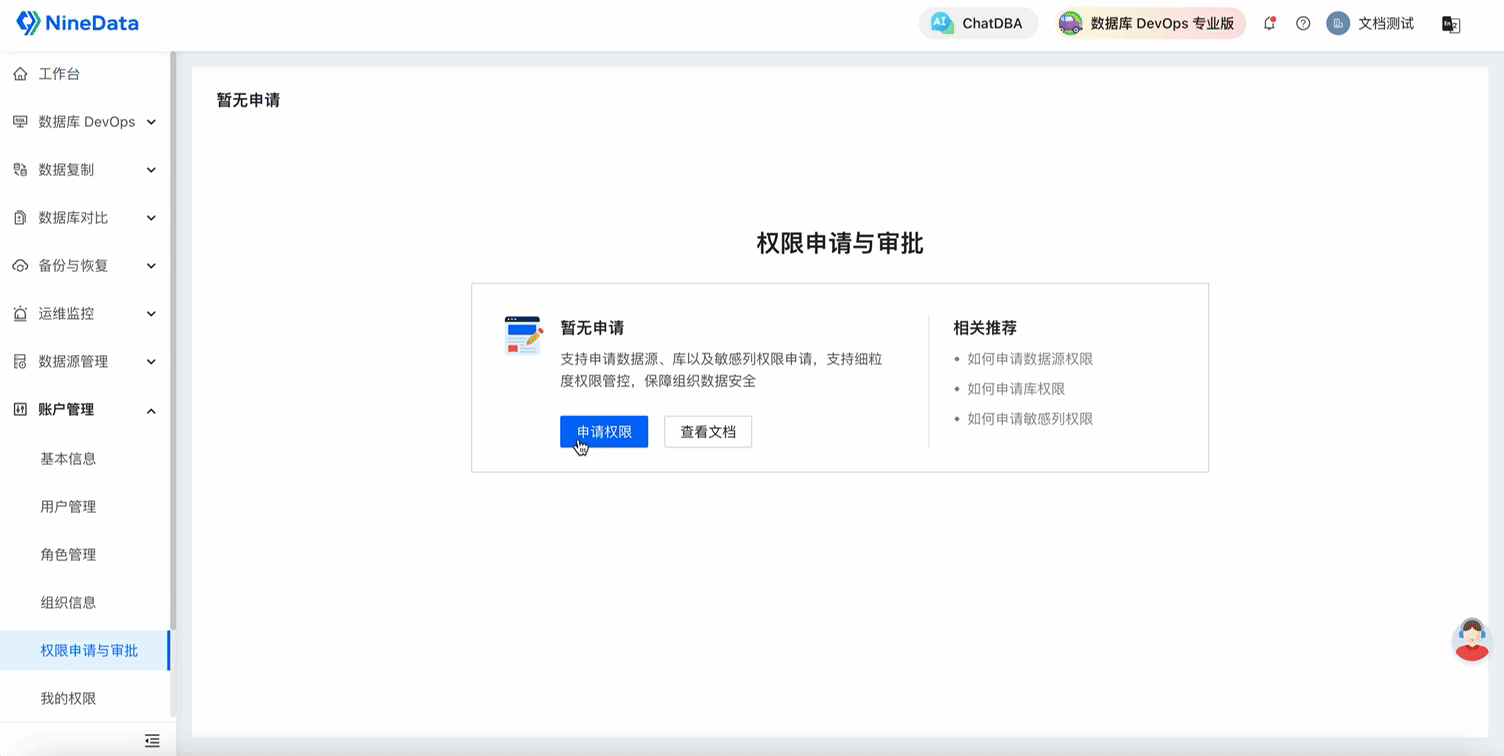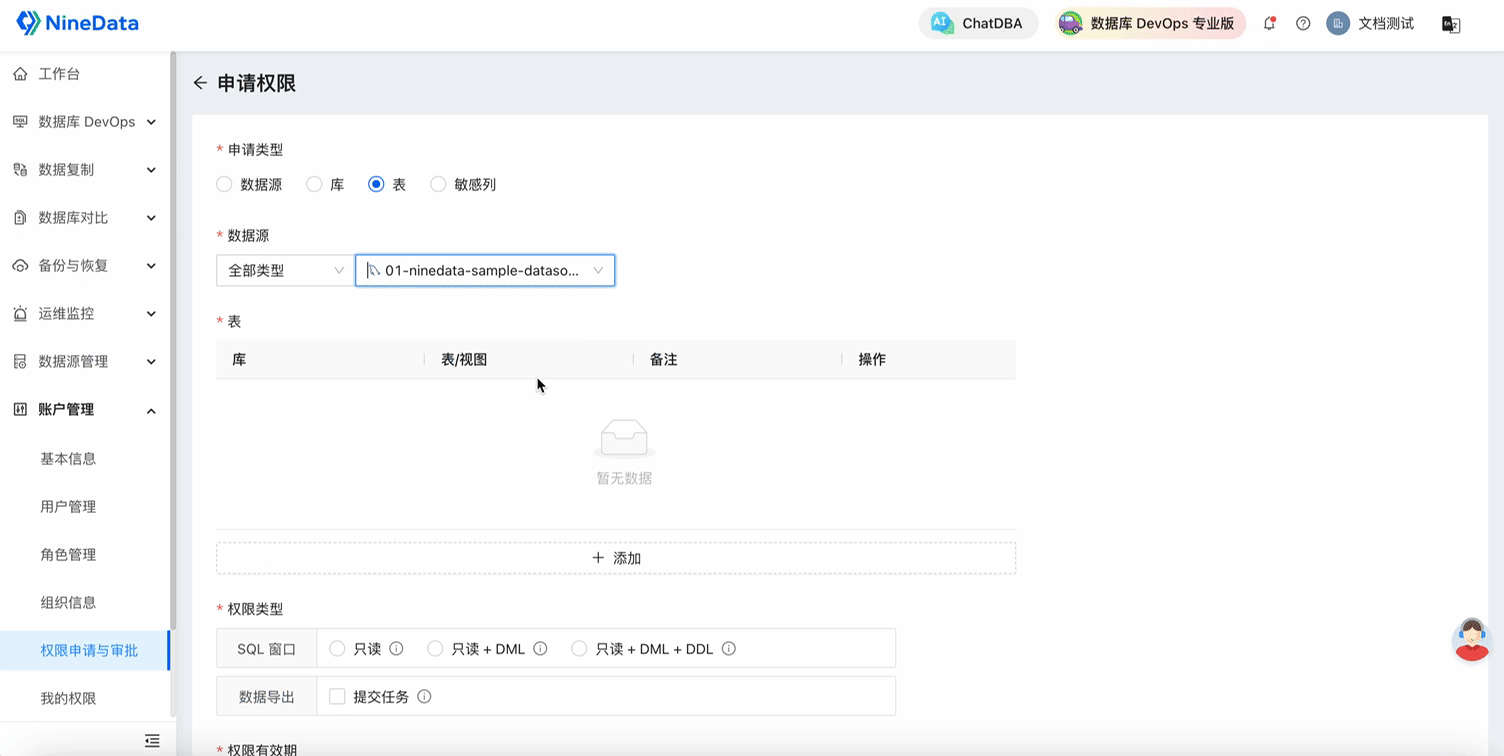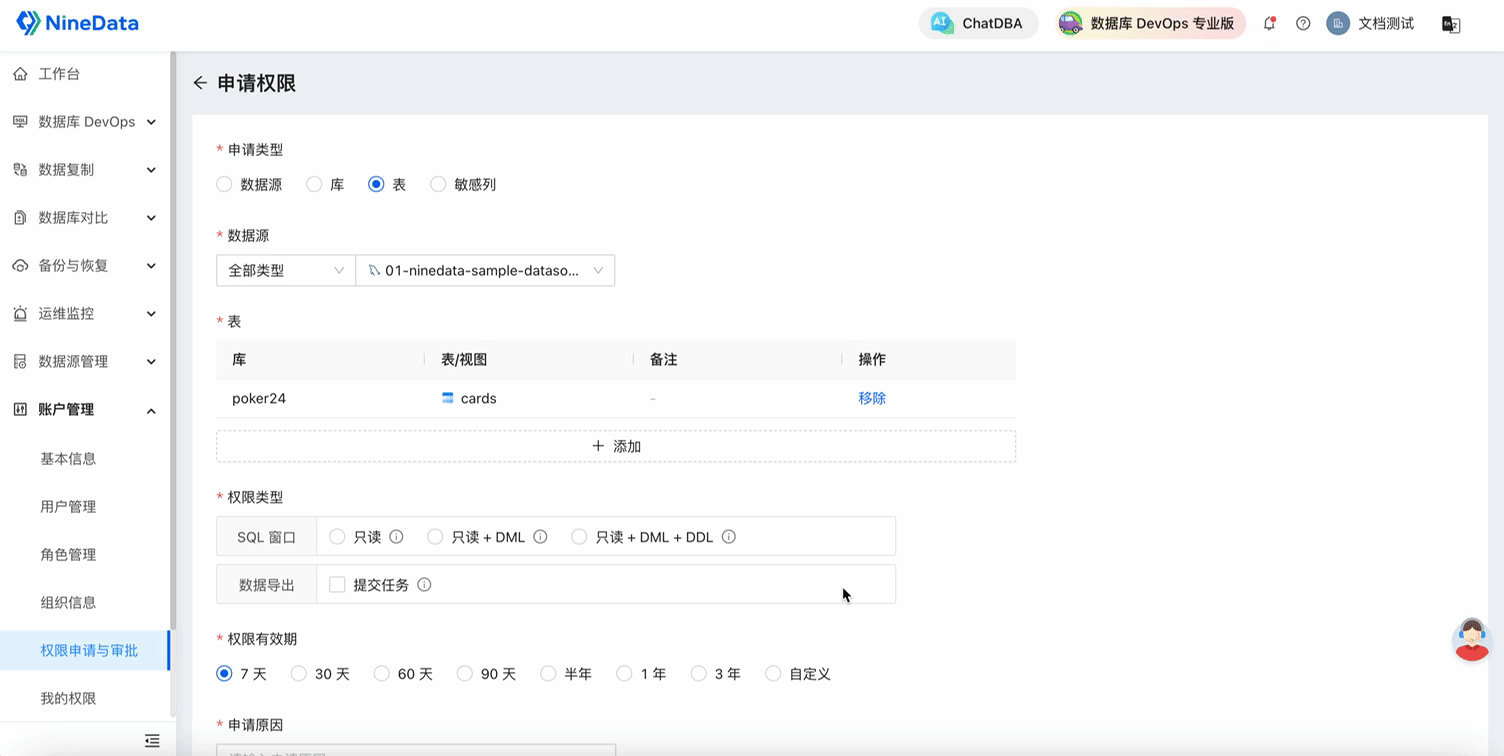
恒等: 如果原因为真, 那么结果必为真.

与: 只有所有原因都为真, 那么结果为真.
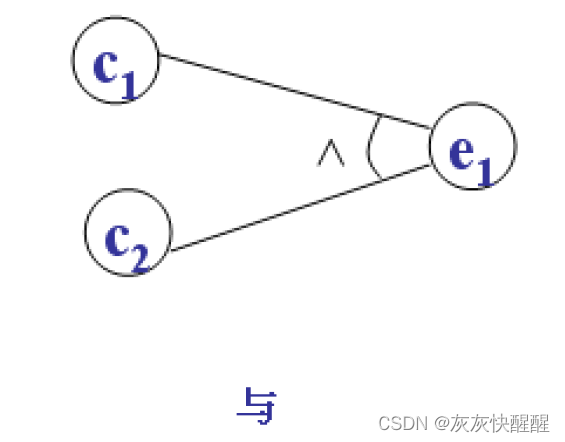
或: 有一个原因为真时, 结果就为真.
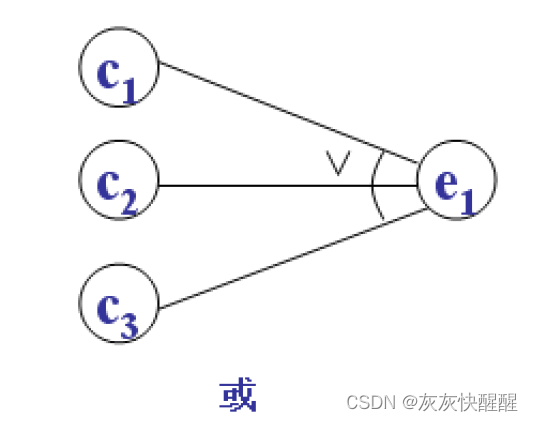
非: 只有原因为假, 结果才为真.
因果图设计测试用例的步骤如下:
(1)分析所有可能的输入和输出.
(2)找出输入和输出之间的因果关系.
(3)画出因果图.
(4)把因果图转换成判定表.
(5)把判定表对应到每一个测试用例.
案例:
假设业务单据的处理规则为: "淘宝618活动, 订单已提交, 订单合计金额大于300元或有红包,则进优惠".
1.对于这条业务规则, 首先通过分析所有的输入和输出, 可得到如下结果:
输入: 订单已提交, 金额大于300元, 有红包
输出: 优惠, 不优惠
2.然后, 第二步, 找出输入和输出之间的因果关系.
(1)订单已提交, 金额大于300元, 有红包 -> 优惠
(2)订单已提交, 金额大于300元, 无红包 -> 优惠
(3)订单已提交, 金额小于300元, 有红包 -> 优惠
(4)订单已提交, 金额小于300元, 无红包 -> 不优惠
(5)订单未提交 -> 不优惠
3.画出因果图
4.其实一般情况下, 当业务逻辑十分复杂时, 因果图会很恶心, 所以我们一般会使用下面的判定表. 这里有三个条件, 两个取值, 所以表的列数为2*2*2 = 8
5.转换成最终的测试用例
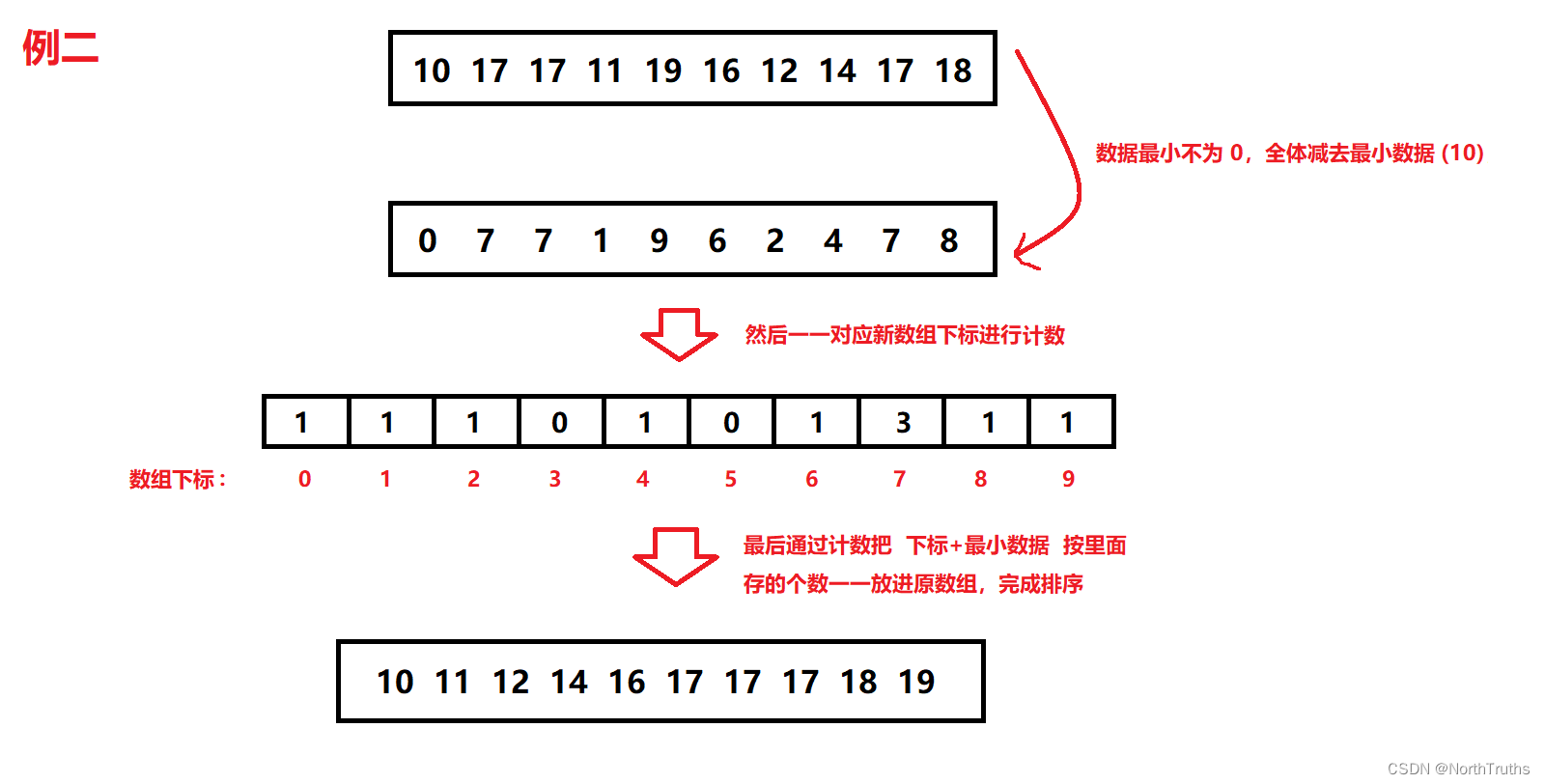
案例二:
以注册的需求为例:
姓名, 邮箱, 密码, 确认密码, 验证码必须全部输入, 才能进行注册.
这时就需要设计2 * 2 * 2 * 2 * 2 = 32条测试用例
因果法设计测试用例可以帮助测试人员理清输入和输出之间的关系, 但对于比较复杂的输入和输出, 会耗费大量的时间.
正交排列
正交法的目的是为了减少测试用例的数目. 用尽可能少的用例覆盖输入的两两组合.
正交试验设计是研究多因素多水平的一种设计方法, 它根据正交性, 因试验因素的全部水平组合中挑选出部分有代表性的具有实验, 通过对这部分实验结果的分析了解全面试验的情况, 找出最优的水平组合. 正交试验设计是一种基于正交表的, 高效率, 快速, 经济的试验.
因素: 在一项实验中, 凡欲考察的变量称为因素(变量).
水平: 在试验范围内, 因素被考察的值称为水品(变量的取值).
正交表的构成:
行数: 正交表中行的个数, 即试验的次数, 用N代表.
因素数: 正交表中列的个数, 用C代表.
水平数: 任何单个因素能够取得的值的最大个数, 用T代表.
正交表的表示形式: L = 行数(水平数 * 因素数) L= N(TC) 行数 = 因素数 * (水平数 - 1) + 1
正交表的两条性质: (1)每一列中各数字出现次数都一样多.
(2)任何两列中各有序数对出现的次数都一样多. (比如挑出任何两列, 其序列为 1, 2, 则在其它行中, 该两列不会再出现为1, 2的序列).
正交法设计测试用例的步骤:
1. 有哪些因素(变量)
2. 每个因素有哪几个水平(变量的取值).
3.选择一个合适的正交表.
4.把变量的值映射到表中.
5.把每一行的各因素水平的组合作为一个测试用例.
6.加上你认为可以且没有在表出现的用例集合.
案例: 继续以注册为例:
1.因素: 姓名, 邮箱, 密码, 确认密码, 验证码.
2.水平: 填写, 不填写
3. 表中的因素数 = 5;
表中至每个因素数的水平数 = 2.
行数 = (2 - 1) * 5 + 1 -> L = 6(25)
选择正交表, 这里选择了L6_2_5.
4.生成测试用例(这里使用工具allpairs)直接生成正交表即可.
注: ~可以表示填写或者不填写
5.增补测试用例
姓名, 邮箱, 密码, 确认密码, 验证码都不填写.
具体的设计方法 -- 白盒测试
介绍
定义: 白盒测试也叫逻辑驱动测试, 它是对程序的逻辑结构进行检查, 从中获取测试数据.
核心: 对程序的逻辑结构进行检查, 从中获取测试数据.
判定标准: "穷举路径测试" -> 使用测试用例执行了程序流中所有可能的执行流路径, 程序可以得到完全测试.
穷举路径测试可能出现的问题:
1.不同逻辑路径的数量可能达到天文数字.
2.虽然可以测试到程序中的所有路径, 但是程序中可能存在着错误.
原因:(1)即使是穷举路径测试也不能保证程序符合其设计规范. eg: 升序排序写成降序排序.
(2)程序可能会因为缺少某些路径而出现问题. 穷举路径测试当然不能发现缺少了哪些问题.
(3)可能不会暴露敏感问题.
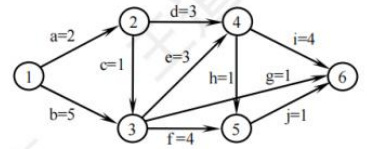
以下所有的测试用例都将使用一个栗子来说, 如下:
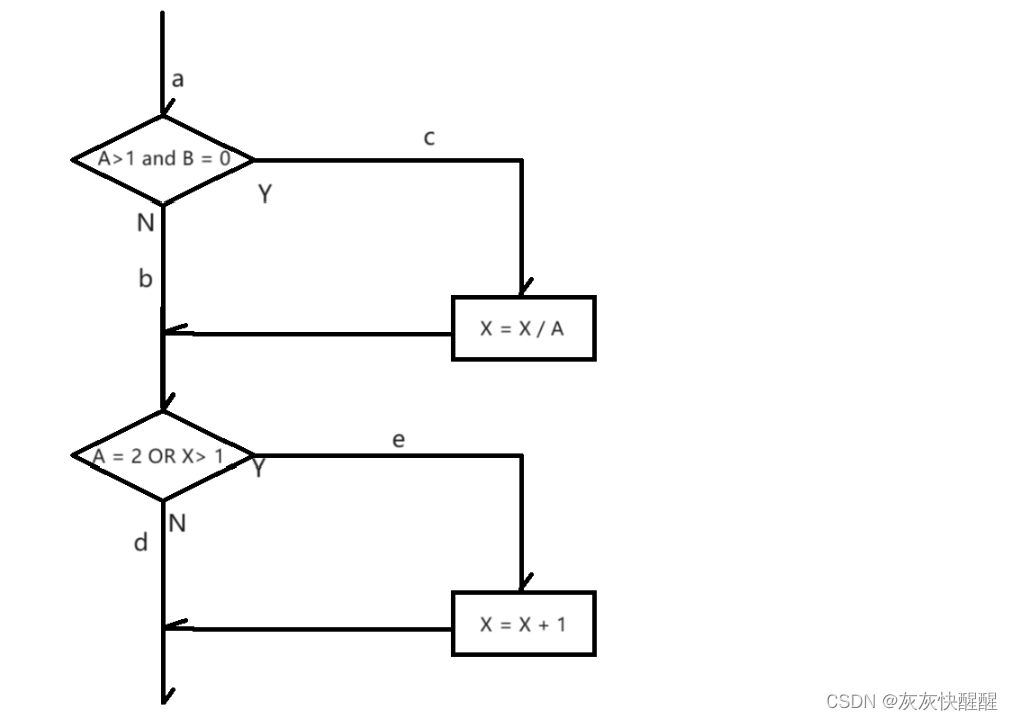
public void foo(int a, int b, int x) {if(A > 1 && B == 0) {X = X / A;}if(A == 2 || X > 1) {X = X + 1;}
}先给出逻辑运行图:
语句覆盖
语句覆盖就是指将程序中的每个语句都至少执行一次. 遗憾地是, 这恰是合理的白盒测试中较弱的准则.
通过编写单个测试用例遍历程序路径ace,可以执行到每一条语句, 也就是说, 通过在a点设置A = 2, B = 0, X = 3. 每条语句都将被执行一次(这里X可以取任意值).
遗憾的是, 这个准则相当不足. 举例来说, 也许第一个判断应是"或", 而不是"与"(比如或后面情况对X或者A,B两个值有影响, 那么就不好说了), 如果这样这个错误, 就发不现.
因此, 语句覆盖这条准则有很大的不足, 以至于它通常没有什么用处.
判定覆盖/分支覆盖
定义: 判定覆盖/分支覆盖是较强一些的逻辑准则. 要求编写足够的测试用例, 使得每一个判断至少有一个为真/为假的输出结果.(每条分支路径至少应该遍历一次). 分支或判定语句的栗子包括switch, do-while和if-else语句.
判定覆盖通常可以满足语句覆盖. 由于每条语句都是在要么从分支语句开始, 要么从程序入口点开始的某条子路径上, 如果每条分支路径都被执行到了, 那么每条语句也应该执行到了. 但仍然有三种例外的情况.
程序中不存在判断.
程序或子程序/方法有着多重入口点. 只有从程序特定入口点进入时, 某条特定的语句才能执行到.
在ON单元里的语句. 遍历每条分支路径并不一定能确保所有的ON单元被执行到.
在逻辑运行图中, 两个覆盖了路径ace和abd, 或涵盖了路径acd和abe的测试用例就可以满足判定覆盖的要求. eg: A = 3, B = 0, X = 3和A = 2, B = 1, X = 1.
判定覆盖是一种比语句覆盖更强的准则, 但仍然有所不足. 举例来说, 我们仅有50%的可能性遍历到那条X未发生变化的路径. 比如说第二个判断出现错误(X > 1 写成 X < 1),那么前面的测试用例都无法找出这个错误.
条件覆盖
在条件覆盖的情况下, 要编写足够多的测试用例以确保将判断中的每个条件的所有可能结果至少执行一次. 因为就如同判定覆盖的情况一样, 这并不总是能让每条语句都执行到, 因此作为对这条准则的补充就是对程序或者子程序, 包括ON单元的每一个入口点都至少调用一次.
在本条案例中就是指, 起码要走到判定条件的最后一个, 即前面的判定条件都不能判定为真.
eg: 1. A = 3, B = 0, X = 4 -> ace 2. A = 1, B = 1, X = 1 -> adb.
虽然条件覆盖准则乍看上去似乎满足了判定覆盖准则, 但并不总是如此. 如果正在测试判断条件IF(A&B), 条件覆盖准则将要求编写的测试用例: A为真, B为假并不能使得If语句中的then被执行到.
判定/条件覆盖
显然, 解决条件覆盖的问题的方案就是所谓的判定/条件覆盖准则. 这准则要求设计出充足的测试用例, 将一个判断中的每个条件的所有可能结果都至少执行一次(每个条件都要有Y/N两种判断), 将每个入口点都至少调用一次.
但是我们之前也学过 && 和 || , 它们的"短路"性质可能会屏蔽掉或阻碍其它的条件. 就比如在 && 中, 如果一个为假, 后面的语句都将不再执行. 在 || 中, 如果一个条件为真, 则后面的语句都不再执行. 因此, 条件覆盖或判定/条件覆盖准则不一定能发现逻辑表达式中的错误.
多重条件覆盖准则
所谓的多重条件覆盖准则能够部分解决这个问题. 该准则要求编写足够多的测试用例, 将每个判定中的所有可能的条件组合, 以及所有的入口点都执行一次. 并且, 很容易发现, 满足多重条件覆盖准则的测试用例集, 同样满足判定覆盖原则, 条件覆盖准则以及判定/条件覆盖准则.
如果是多重条件覆盖准则, 那么它又将之前的执行流程图进一步细化了:
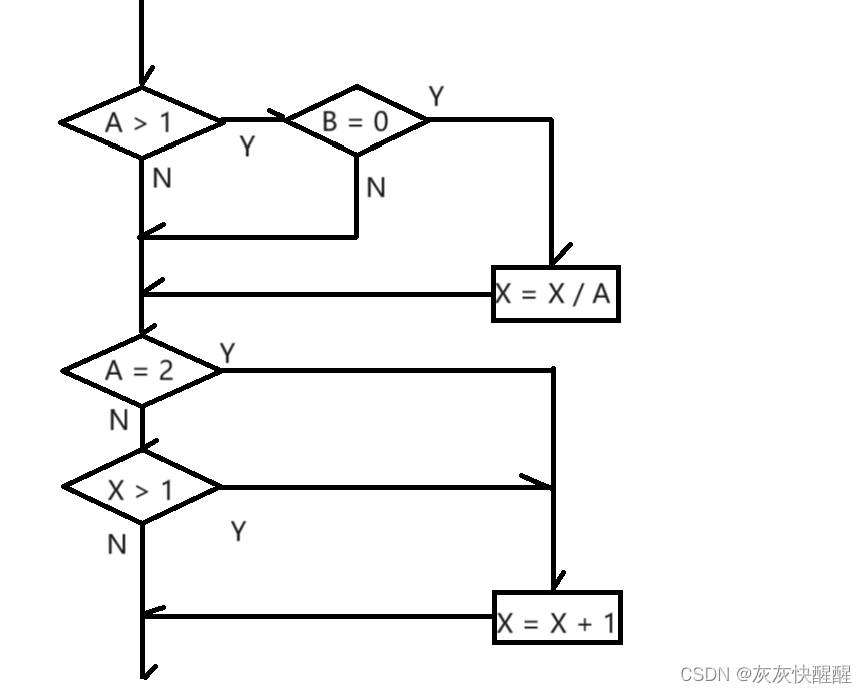
再次回到测试用例设计中, 它必须覆盖一下8种组合(但是测试用例不一定非得设计八种):
1.A > 1, B = 0
2.A > 1, B <> 0
3.A <= 1, B = 0
4.A <= 1, B <> 0
5.A = 2, X > 1
6.A = 2, X <= 1
7.A <> 2, X > 1
8.A <> 2, X <= 1
总的说来, 对于包含每个判断只存在一种条件的程序, 最简单的测试准则就是设计出足够数量的测试用例, 实现: (1)将每个判断的所有结果都至少执行一次; (2) 将所有的程序入口(例如入口点和ON单元)都至少执行一次. 而对于包含多重条件判断的程序, 最简单的测试准则是设计出足够数量的测试用例, 将每个判断的所有可能的条件结果组合, 以及所有的入口点都至少执行一次.