AcWing 4405. 统计子矩阵：做题笔记

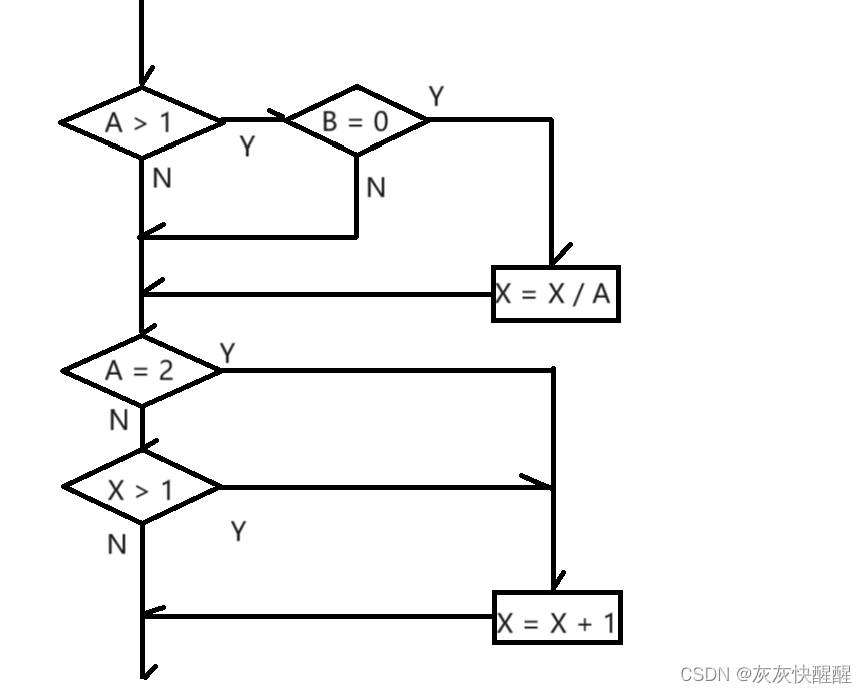
暴力思路

代码

前缀和+双指针

代码

解释

推荐博客

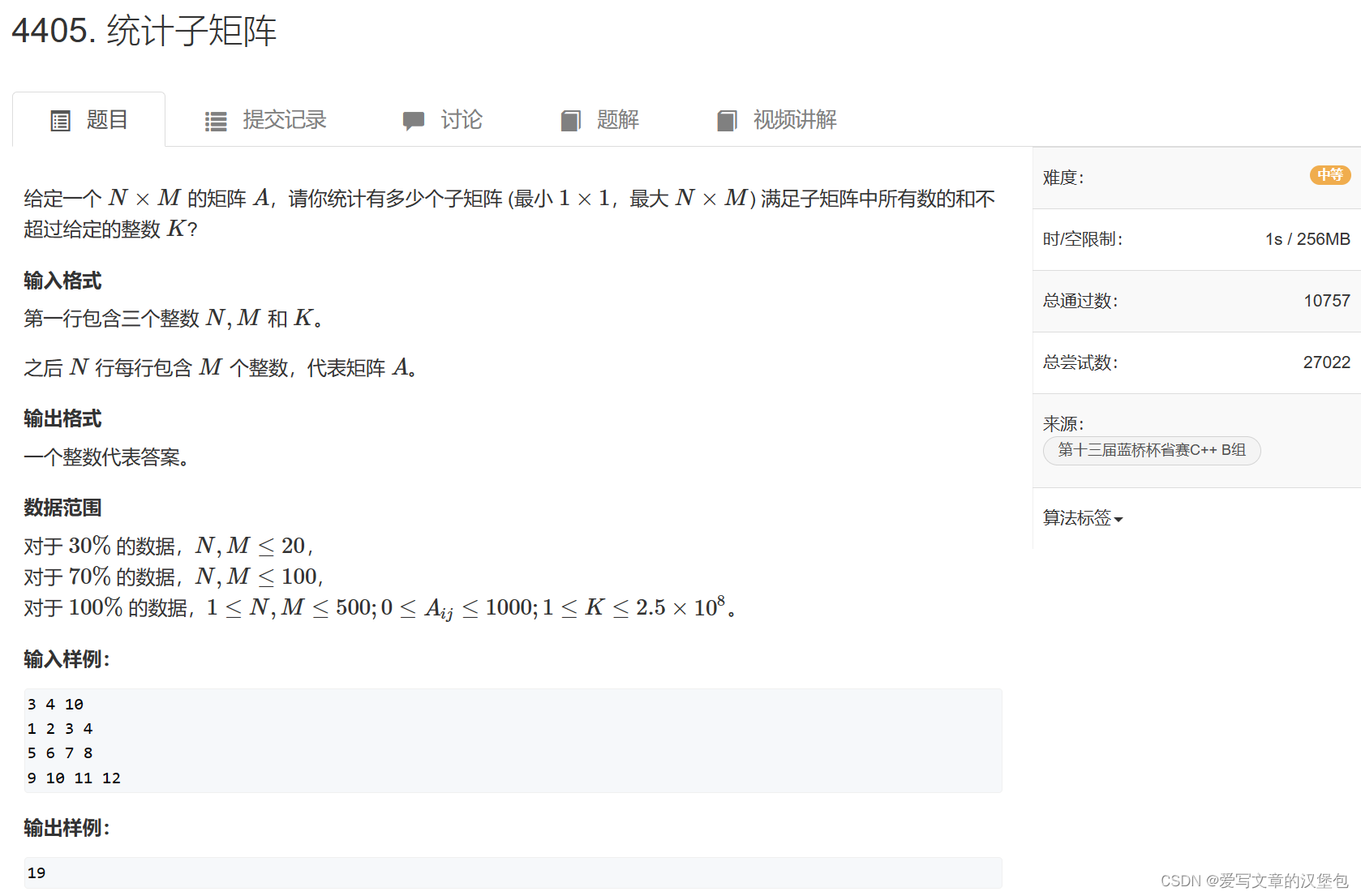
这道题的主要思路就是枚举所有的子矩阵，判断符合条件的子矩阵的个数。

暴力思路

我服了，其实我最开始没有想到：枚举所有的子矩阵 这样一个很有总结性的要点。

我是想着哦我先知道这道题是考二维前缀和的，然后与模板不同的是，这里并没有给出(额也不算没有给出吧)一维前缀和里面 l r 边界中的 l，这样形容可以理解嘛？像激光炸弹那道题里：

这句话就是给出了左上角的点，我们知道二维前缀和求某个子矩阵的和就是用前缀和数组中右下角-左上角。

但这道题里没有直接说，我看样例解释之后明白他是需要遍历所有1*1/1*2/...2*1/2*2...，这样，然后我觉得在正常的求某个子矩阵的和的基础上，需要在原来的两层循环内在遍历(1*1/1*2/...2*1/2*2...)这些所有的可能，然后就套了4层循环。写了暴力。

我的暴力是这样写出来的😂哎甚至是暴力都写得很艰难啊🥀🤣

代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N=510;
int q[N][N];
int n,m,k;
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>k;int cnt=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>q[i][j];q[i][j]+=q[i-1][j]+q[i][j-1]-q[i-1][j-1];//cout<<q[i][j]<<" ";}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int z=1;z<=i;z++){for(int y=1;y<=j;y++){int t=q[i][j]-q[z-1][j]-q[i][y-1]+q[z-1][y-1];if(t<=k){cnt++;}}}}}cout<<cnt;return 0;
}

因为写了四层循环，500^4，肯定会超时了。

这样是能过6/10个数据，真比赛写到这就算了吧😂别的我也写不出来doge(流下了苦涩的眼泪😂)

前缀和+双指针

这个先看代码把

代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N=510;
int n,m,k;
int q[N][N];
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>k;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>q[i][j];q[i][j]+=q[i-1][j];//计算出每一列的前缀和矩阵 }}long long cnt=0;for(int i=1;i<=n;i++){for(int j=i;j<=n;j++)//枚举上下边界 {for(int l=1,r=1,sum=0;r<=m;r++)//左右边界的滑动窗口 {//当符合题目所说的<=k时，我们就拓宽右边界 sum+=q[j][r]-q[i-1][r];//添加上r边界端点的子矩阵的和 //不符合的时候，我们就要把左边界向右移动 while(sum>k){sum-=q[j][l]-q[i-1][l];//减去移出去的左端点处的和l++;}//每次窗口的移动所得到的满足条件子矩阵的个数 =右边界 r 减去左边界 l 再加上 1cnt+=r-l+1;}}} cout<<cnt;return 0;
}

解释

这里我们的思路是：

计算出这个二维矩阵每一列的前缀和的二维矩阵。

我们可以把这个二维矩阵的每一列看作一维前缀和数组中的每一位数字，这个数字实际代表的是一列的前缀和。

我们想要判断这个一维数组所有的子区间是否符合题目条件，

①要么我们暴力枚举所有的子区间：

// 如果计算a数组所有子区间的和,p数组为其预处理出的前缀和
//(这里用前缀和算是为了简写，主要突出两种写法大框架上的区别，否则最内层还有一层计算子区间和的循环)for(int l=1; l<=n; l++)
{for(int r=i; r<=n; r++){sum=p[r]-p[l-1];// 按题目要求对 sum 进行判断}
}

在暴力枚举的方法中，我们需要枚举所有可能的子区间，然后对每个子区间进行检查。这通常需要两层循环，第一层循环枚举子区间的起始位置，第二层循环枚举子区间的结束位置。然后在这两层循环内部，我们计算子区间的和，并进行判断。

②要么就是利用滑动窗口：

int l = 1, r = 1, sum = 0;// 使用 for 循环遍历数组
for (r= 1; r < n; r++) {// 将右边界的元素加入窗口sum += a[r];// 使用 while 循环移动左边界，直到窗口内的和满足条件while (sum > k && l < r) {sum -= a[l];l++;}//对窗口内的和进行判断
}

让这个窗口在数组上滑动，每次滑动都会有一个元素进入窗口，同时有一个元素离开窗口。通过这种方式，我们可以在每次窗口滑动时，快速地更新窗口内的信息，而不需要对整个窗口进行重新计算。

(暴力和滑动窗口的区别主要在外层的两个循环上，而不在于计算这些和上，因为是正是由于外层的两层循环才导致了重复计算的和。)

在每一种确定的上下边界里，通过滑动窗口调整左右边界，这样就把两层循环降成一层。

因此我们每次对这个一维数组的边界的变动就会构成 r-l+1 个不同的子矩阵。

我们拓宽右边界，也就是把右端点添加到序列中，从 l~r 的每一个元素加上了 r 都形成了一个新的子区间，在二维里也就是都形成了一个新的子矩阵。因此新增加的包含该列的新的子矩阵的数量就是r-l+1即区间内元素数量

我们在最外层需要有两个for循环一层 i 循环掌管上边界，一层 j 循环掌管下边界，这个下边界是>=上边界的，因此它的初值可以直接从 i 开始。这样就保证了遍历到所有的子矩阵。