文章目录
- 1 问题描述
- 2 启发式搜索
- 3 A*算法
- 3.1 参考网址
- 3.2 是什么
- 3.3 为什么A*算法适用于八数码问题
- 3.4 A* 算法的基本框架
- 4 A* 算法如何解决八数码问题
- 4.1 八数码状态的存储
- 4.2 启发式函数
- 4.3 构造目标状态元素位置的字典
- 4.4 在二维列表中查找目标元素
- 4.5 A* 算法主体
- 4.6 路径构造函数
- 4.7 函数调用
- 4.8 全部代码
- 4.9 运行结果
- 5 拓展:八数码问题有无解的讨论
- 5.1 逆序
- 5.2 逆序奇偶性与可解性
- 5.3 逆序不变性
1 问题描述
-
八数码问题是经典的启发式搜索问题,其目标是将一个3x3的九宫格中的数字1-8以及一个空格,按照规定的移动规则,通过移动操作,最终达到特定的顺序状态,通常是按照数字顺序排列,如下:
1 2 3
4 5 6
7 8 _ -
八数码问题的变种包括:
- 15 数码问题:与八数码类似,但是在4x4的九宫格中利用数字1-15及一个空格进行移动
- n 数码问题:可以扩展到更大规模,例如n×n的九宫格,其中包含数字1至n×n-1以及一个空格,玩家需要重新排列数字以达到特定的状态
2 启发式搜索
- 传统搜索算法通常不考虑启发信息,仅仅依赖于逐步尝试可能的方案,逐渐扩展搜索空间,直到找到解决方案或最优解,比如BFS、DFS等等。在大规模问题或者复杂问题中,这些传统搜索算法可能会因为搜索空间过大而导致效率低下
- 启发式搜索是一种问题求解的方法,它结合了传统的搜索方法和一定的启发信息(heuristic information)来指导搜索方向。启发函数可以评估当前状态与目标状态的相似度,从而指导搜索方向。通过启发式函数的帮助,搜索可以更加偏向于朝着可能更接近最优解的方向前进,而不是盲目地扩展所有可能的搜索路径。
3 A*算法
3.1 参考网址
一个讲A*算法讲得很好的网站:
a-star
3.2 是什么
-
A*算法是一种启发式搜索算法,常用于寻找图中的最短路径或最优解。它结合了广度优先搜索和启发信息,在搜索过程中能够有效地减少搜索空间,从而提高搜索效率。
-
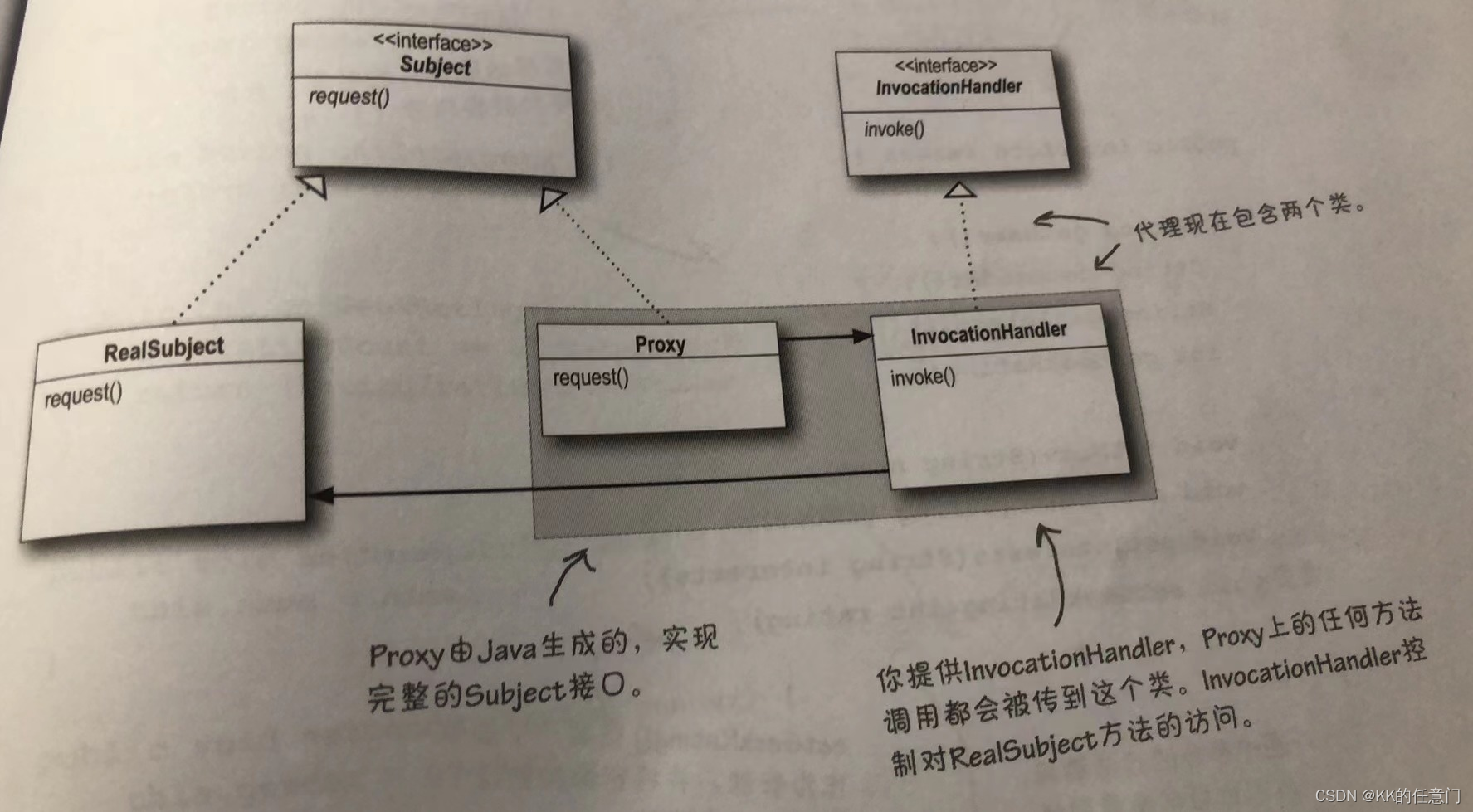
A* 算法的核心思想是综合考虑两个方面的信息:从起始节点到当前节点的实际代价(通常是已经走过的路径的代价),以及从当前节点到目标节点的估计代价(启发式函数)。这两方面的信息通过综合起来选择估计代价最小的节点进行搜索,朝着目标节点前进。

A*算法同时考虑了从起始节点到当前节点的实际代价,以及从当前节点到目标节点的估计代价(上图)
3.3 为什么A*算法适用于八数码问题
- A* 算法适用于图搜索问题,本质上,八数码问题的每一种状态都可以看成是图中的一个节点,所以可以使用A* 算法求解
- 在这里,从起始节点到当前节点的实际代价为从起始状态到当前状态的步骤数,而从当前节点到目标节点的估计代价我们使用当前状态到目标状态的曼哈顿距离来估计
在二维坐标系中,两点 (x1, y1) 和 (x2, y2) 之间的曼哈顿距离可以用以下公式表示: Manhattandistance = ∣x2−x1∣+∣y2−y1∣
这里我们计算八数码中每一个元素到其最终位置的曼哈顿距离的和作为当前状态到目标状态的曼哈顿距离
3.4 A* 算法的基本框架
- 主体
def search_with_priority_queue(graph, start, goal, heuristic):"""使用优先队列进行搜索的函数参数:graph: 表示图的数据结构start: 起始节点goal: 目标节点heuristic: 启发式函数返回值:came_from: 包含每个节点的前驱节点信息的字典cost_so_far: 到达每个节点的当前最小成本路径的字典"""# 创建一个优先队列,用于存储待探索的节点frontier = PriorityQueue()# 将起始节点 start 加入到优先队列中,并将其优先级设为 0frontier.put(start, 0)# 创建一个字典,用于记录每个节点的前驱节点came_from = {}# 创建一个字典,用于记录到达每个节点的当前最小成本路径cost_so_far = {}# 初始化起始节点的前驱为 None,并将到达起始节点的成本设为 0came_from[start] = Nonecost_so_far[start] = 0# 进入一个 while 循环,直到 frontier 中不再有待探索的节点while not frontier.empty():# 从优先队列中取出优先级最高的节点作为当前节点current = frontier.get()# 判断当前节点是否为目标节点,如果是,则退出循环if current == goal:break# 遍历当前节点的相邻节点 nextfor next in graph.neighbors(current):# 计算从起始节点到 next 节点的成本new_cost = cost_so_far[current] + graph.cost(current, next)# 如果 next 节点尚未在 cost_so_far 中记录或者新成本小于之前记录的成本if next not in cost_so_far or new_cost < cost_so_far[next]:# 更新 cost_so_far 中 next 节点的成本cost_so_far[next] = new_cost# 计算从起始节点到 next 节点的启发式估计成本,并将其作为优先级priority = new_cost + heuristic(goal, next)# 将 next 节点加入到优先队列中,并设置其优先级frontier.put(next, priority)# 更新 came_from 中 next 节点的前驱节点为当前节点 currentcame_from[next] = currentreturn came_from, cost_so_far
- 根据前驱字典 came_from 构造出找到的路径
def generate_path(start, goal, came_from):"""生成路径的函数参数:start: 起点位置goal: 终点位置came_from: 包含每个位置的前驱位置信息的字典返回值:path: 从起点到终点的路径列表"""current = goal # 将当前位置设置为终点path = [] # 初始化路径为空列表if goal not in came_from:print("无解")return [] # 如果终点没有前驱位置,直接返回空路径while current != start: # 当前位置不是起点时执行循环path.append(current) # 将当前位置添加到路径中current = came_from[current] # 更新当前位置为其前驱位置path.append(start) # 将起点添加到路径中(可选)path.reverse() # 反转路径,将起点放在第一个位置(可选)return path
4 A* 算法如何解决八数码问题
使用python进行编程。
4.1 八数码状态的存储
在 python 中,我们使用二维列表进行八数码初始状态和目标状态的存储
# 初始状态
initial_state = [[1, 2, 3],[4, 5, 6],[0, 7, 8]
]# 目标状态
goal_state = [[1, 2, 6],[4, 5, 8],[7, 0, 3]
]
4.2 启发式函数
从当前节点到目标节点的估计代价我们使用当前状态到目标状态的曼哈顿距离来估计,这里我们计算八数码中每一个元素到其最终位置的曼哈顿距离的和作为当前状态到目标状态的曼哈顿距离
def manhattan_distance(state, goal_map):"""计算曼哈顿距离参数:state (list): 表示当前状态的二维列表。goal_map (dict): 将数值映射到其在目标二维列表中索引的字典。返回:int: 当前状态与目标状态之间的曼哈顿距离。"""distance = 0for i in range(len(state)):for j in range(len(state[0])):value = state[i][j]if value != 0:goal_pos = goal_map[value]distance += abs(i - goal_pos[0]) + abs(j - goal_pos[1])return distance
4.3 构造目标状态元素位置的字典
- 在启发式函数中,传入的参数是当前状态的二维列表,以及目标状态元素位置的字典
- 因为当前状态每次传入的参数都不一定,所以使用二维列表;而目标状态是固定的,所以使用一个字典进行元素位置的记录,提高启发式函数中曼哈顿函数的计算效率
def index_mapping_2d(lst):"""创建一个将数值映射到其在二维列表中索引的映射关系。参数:lst (list): 一个二维数值列表。返回:dict: 一个字典,其中键是二维列表中的数值,值是它们在列表中的索引的元组。"""index_map = {}for i in range(len(lst)):for j in range(len(lst[i])):val = lst[i][j]index_map[val] = (i, j)return index_map
4.4 在二维列表中查找目标元素
在寻找路径的过程中,我们通过空位(此处用0代表)的移动来进行边界的扩展,所以在每次移动之前都要找到元素0的位置,于是我们需要一个在二维列表中查找目标元素的函数
def find_element_in_2d_list(arr, target):"""在二维列表中查找目标元素:param arr: 二维列表,待查找的目标元素所在的列表:param target: 目标元素,要在二维列表中查找的元素:return: 如果目标元素存在于二维列表中,则返回其索引 (i, j);如果目标元素不存在,则返回 None"""for i in range(len(arr)):for j in range(len(arr[i])):if arr[i][j] == target:return i, jreturn None
4.5 A* 算法主体
有几个注意点:
- 优先队列的使用:
使用优先队列(小顶堆)存储下一个要检查的状态,以优先级(此处为成本)排序,数字小(成本低)的先进行检查
import heapq # 优先队列(堆)frontier = [] # 待探索节点(边界),以空的优先队列实现,成本低的先探索
heapq.heappush(frontier, (0, initial_state))
这两句代码的意思是:使用列表作为小顶堆的存储,并使用heapq方法进行小顶堆的构建,(0, initial_state) 中,0为成本(此处因为是初始状态所以成本最低,为0),小顶堆以此排序;而 initial_state 就是初始状态的二维列表
- 哈希表键的处理:
可变对象不可哈希,所以不能作为哈希表的键使用,需要转换为元组才能作为键
came_from = dict() # 记录每个节点的前驱节点
initial_state_tuple = tuple(map(tuple, initial_state))
came_from[initial_state_tuple] = None # 起始状态的前驱状态设置为0
而且注意,此处的 initial_state 是二维列表,需要使用两层 tuple 将每一行也转为 tuple,不能整个转换
- 列表的深拷贝
对当前状态 current 相邻状态的探索中,一般情况下最多有上下左右四个方向可以探索,此时在循环中以 current 为开始计算 next 状态,注意要对 current 进行深拷贝,否则对 next 的操作会修改到 current 的值,导致结果出错
import copyfor direc in zero_move_direcs:next = copy.deepcopy(current)# 将0移动到下一个状态的位置next[new_x_zero][new_y_zero], next[x_zero][y_zero] = next[x_zero][y_zero], next[new_x_zero][new_y_zero]
- 算法主体
def AStar(initial_state, goal_state):"""使用A*算法搜索路径:param initial_state: 初始状态:param goal_state: 目标状态:return: 每个节点的前驱节点字典"""print("__开始进行AStar搜索__")goal_map = index_mapping_2d(goal_state)frontier = [] # 待探索节点(边界),以空的优先队列实现,成本低的先探索heapq.heappush(frontier, (0, initial_state))came_from = dict() # 记录每个节点的前驱节点min_cost = dict() # 记录目前位置探索过的节点的最小成本initial_state_tuple = tuple(map(tuple, initial_state))came_from[initial_state_tuple] = None # 起始状态的前驱状态设置为0min_cost[initial_state_tuple] = 0 # 到达起始状态的成本设置为0zero_move_direcs = [[-1, 0], [1, 0], [0, -1], [0, 1]] # 0的移动方向while frontier: # 进行探索,直到 frontier 中没有待探索的状态_, current = heapq.heappop(frontier) # 探索优先级最高的状态if current == goal_state:break# 遍历当前状态的相邻状态current_state_tuple = tuple(map(tuple, current)) # 当前状态转为tuple以便哈希x_zero, y_zero = find_element_in_2d_list(current, 0) # 找到0所在位置for direc in zero_move_direcs:# 计算下一个状态0所在的位置new_x_zero = x_zero + direc[0]new_y_zero = y_zero + direc[1]# 检查该状态0的位置是否合法if new_x_zero < 0 or new_y_zero < 0 or new_x_zero >= len(initial_state) or new_y_zero >= len(initial_state[0]):continue# 计算从起始状态到next状态的成本,这里由于0不管往哪个方向移动成本都一致,所以next状态成本直接+1即可new_cost = min_cost[current_state_tuple] + 1next = copy.deepcopy(current)# 将0移动到下一个状态的位置next[new_x_zero][new_y_zero], next[x_zero][y_zero] = next[x_zero][y_zero], next[new_x_zero][new_y_zero]next_state_tuple = tuple(map(tuple, next))if next_state_tuple not in min_cost or new_cost < min_cost[next_state_tuple]:# 更新next状态的成本min_cost[next_state_tuple] = new_cost# 使用曼哈顿距离计算next的启发式估计成本(initial到next的准确成本 + next到goal的估计成本)priority_cost = new_cost + manhattan_distance(next, goal_map)# 将next状态以计算出的启发式估计成本加入优先队列中heapq.heappush(frontier, (priority_cost, next))came_from[next_state_tuple] = tuple(map(tuple, current))return came_from
4.6 路径构造函数
- 在A* 搜索完成后,使用返回的 came_from 字典构建从初始状态的目标状态的函数
- 由于八数码问题可能有无解的情况,所以需要判断目标状态是否在 came_from 中,也就是判断是否找到了解
- 由于 came_from 记录的键值对是 “当前节点:前驱节点” ,所以需要从目标状态开始遍历,直到初始状态,最后输出的时候进行反转
def build_path(initial_state, goal_state, came_from):"""构建路径并输出,以找到从初始状态到目标状态的路径。参数:initial_state: 二维列表,代表初始状态goal_state: 二维列表,代表目标状态came_from: 字典,记录每个状态是从哪个状态转移而来返回值:无返回值,直接打印输出路径信息"""# 将二维列表转换为元组initial_state_tuple = tuple(map(tuple, initial_state))goal_state_tuple = tuple(map(tuple, goal_state))current_tuple = goal_state_tuplepath = []have_solution = True# 回溯找到路径while current_tuple != initial_state_tuple:if goal_state_tuple not in came_from:have_solution = Falseprint("无解")breakelse:path.append(current_tuple)current_tuple = came_from[current_tuple]# 如果有解,则输出路径if have_solution:path.append(initial_state_tuple)path.reverse()step = 0for state in path:print("步骤" + str(step))step += 1for row in state:print(row)print()
4.7 函数调用
# 使用A*算法求解路径
came_from = AStar(initial_state, goal_state)
# 进行路径构建
build_path(initial_state, goal_state, came_from)
4.8 全部代码
import heapq # 优先队列(堆)
import copydef manhattan_distance(state, goal_map):"""计算曼哈顿距离参数:state (list): 表示当前状态的二维列表。goal_map (dict): 将数值映射到其在目标二维列表中索引的字典。返回:int: 当前状态与目标状态之间的曼哈顿距离。"""distance = 0for i in range(len(state)):for j in range(len(state[0])):value = state[i][j]if value != 0:goal_pos = goal_map[value]distance += abs(i - goal_pos[0]) + abs(j - goal_pos[1])return distancedef index_mapping_2d(lst):"""创建一个将数值映射到其在二维列表中索引的映射关系。参数:lst (list): 一个二维数值列表。返回:dict: 一个字典,其中键是二维列表中的数值,值是它们在列表中的索引的元组。"""index_map = {}for i in range(len(lst)):for j in range(len(lst[i])):val = lst[i][j]index_map[val] = (i, j)return index_mapdef find_element_in_2d_list(arr, target):"""在二维列表中查找目标元素:param arr: 二维列表,待查找的目标元素所在的列表:param target: 目标元素,要在二维列表中查找的元素:return: 如果目标元素存在于二维列表中,则返回其索引 (i, j);如果目标元素不存在,则返回 None"""for i in range(len(arr)):for j in range(len(arr[i])):if arr[i][j] == target:return i, jreturn Nonedef AStar(initial_state, goal_state):"""使用A*算法搜索路径:param initial_state: 初始状态:param goal_state: 目标状态:return: 每个节点的前驱节点字典"""print("__开始进行AStar搜索__")goal_map = index_mapping_2d(goal_state)frontier = [] # 待探索节点(边界),以空的优先队列实现,成本低的先探索heapq.heappush(frontier, (0, initial_state))came_from = dict() # 记录每个节点的前驱节点min_cost = dict() # 记录目前位置探索过的节点的最小成本initial_state_tuple = tuple(map(tuple, initial_state))came_from[initial_state_tuple] = None # 起始状态的前驱状态设置为0min_cost[initial_state_tuple] = 0 # 到达起始状态的成本设置为0zero_move_direcs = [[-1, 0], [1, 0], [0, -1], [0, 1]] # 0的移动方向while frontier: # 进行探索,直到 frontier 中没有待探索的状态_, current = heapq.heappop(frontier) # 探索优先级最高的状态if current == goal_state:break# 遍历当前状态的相邻状态current_state_tuple = tuple(map(tuple, current)) # 当前状态转为tuple以便哈希x_zero, y_zero = find_element_in_2d_list(current, 0) # 找到0所在位置for direc in zero_move_direcs:# 计算下一个状态0所在的位置new_x_zero = x_zero + direc[0]new_y_zero = y_zero + direc[1]# 检查该状态0的位置是否合法if new_x_zero < 0 or new_y_zero < 0 or new_x_zero >= len(initial_state) or new_y_zero >= len(initial_state[0]):continue# 计算从起始状态到next状态的成本,这里由于0不管往哪个方向移动成本都一致,所以next状态成本直接+1即可new_cost = min_cost[current_state_tuple] + 1next = copy.deepcopy(current)# 将0移动到下一个状态的位置next[new_x_zero][new_y_zero], next[x_zero][y_zero] = next[x_zero][y_zero], next[new_x_zero][new_y_zero]next_state_tuple = tuple(map(tuple, next))if next_state_tuple not in min_cost or new_cost < min_cost[next_state_tuple]:# 更新next状态的成本min_cost[next_state_tuple] = new_cost# 使用曼哈顿距离计算next的启发式估计成本(initial到next的准确成本 + next到goal的估计成本)priority_cost = new_cost + manhattan_distance(next, goal_map)# 将next状态以计算出的启发式估计成本加入优先队列中heapq.heappush(frontier, (priority_cost, next))came_from[next_state_tuple] = tuple(map(tuple, current))return came_fromdef build_path(initial_state, goal_state, came_from):"""构建路径并输出,以找到从初始状态到目标状态的路径。参数:initial_state: 二维列表,代表初始状态goal_state: 二维列表,代表目标状态came_from: 字典,记录每个状态是从哪个状态转移而来返回值:无返回值,直接打印输出路径信息"""# 将二维列表转换为元组initial_state_tuple = tuple(map(tuple, initial_state))goal_state_tuple = tuple(map(tuple, goal_state))current_tuple = goal_state_tuplepath = []have_solution = True# 回溯找到路径while current_tuple != initial_state_tuple:if goal_state_tuple not in came_from:have_solution = Falseprint("无解")breakelse:path.append(current_tuple)current_tuple = came_from[current_tuple]# 如果有解,则输出路径if have_solution:path.append(initial_state_tuple)path.reverse()step = 0for state in path:print("步骤" + str(step))step += 1for row in state:print(row)print()# 初始状态
initial_state = [[1, 2, 3],[4, 5, 6],[0, 7, 8]
]# 目标状态
goal_state = [[1, 2, 6],[4, 5, 8],[7, 0, 3]
]# 使用A*算法求解路径
came_from = AStar(initial_state, goal_state)
# 进行路径构建
build_path(initial_state, goal_state, came_from)
4.9 运行结果
- 当有解时,是下面的形式,无解则直接显示 “无解”
__开始进行AStar搜索__
步骤0
(1, 2, 3)
(4, 5, 6)
(0, 7, 8)步骤1
(1, 2, 3)
(4, 5, 6)
(7, 0, 8)......
进程已结束,退出代码为 0
5 拓展:八数码问题有无解的讨论
5.1 逆序
- 将八数码问题的状态表示成一维形式,即从左到右依次排列 9 个数字。
- 除 0 之外的每个数字前面比它大的数字的个数,称为该数字的逆序数。
- 一个状态的逆序,是指所有数字的逆序数之和。
5.2 逆序奇偶性与可解性
- 若两个状态的逆序奇偶性相同,则这两个状态可相互到达。
- 若两个状态的逆序奇偶性不同,则这两个状态不可相互到达。
5.3 逆序不变性
- 左右移动空格不会改变逆序。
- 上下移动空格相当于将一个数字向前(或向后)移动两格,跳过两个数字。
- 若跳过的两个数字都比它大(或小),则逆序可能增加或减少 2。
- 若跳过的两个数字一个较大一个较小,则逆序不变。





![[Python学习篇] Python解释器](https://img-blog.csdnimg.cn/direct/797a3efdc79a497fb10cbad549244894.png)
![[蓝桥杯练习]通电](https://img-blog.csdnimg.cn/direct/f58214a38e02480b848dd66f4ab6038e.png)