树概述
树类似于现实生活中倒置的树。任何一颗非空树只有一个根节点。一棵树具有以下特点:
- 一棵树中的任意两个结点有且仅有唯一的一条路径连通。
- 一棵树如果有 n 个结点,那么它一定恰好有 n-1 条边。
- 一棵树不包含回路。
下图就是一颗树,并且是一颗二叉树。

如上图所示,通过上面这张图说明一下树中的常用概念:
- 节点:树中的每个元素都可以统称为节点。
- 根节点:顶层节点或者说没有父节点的节点。上图中 A 节点就是根节点。
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。上图中的 B 节点是 D 节点、E 节点的父节点。
- 子节点:一个节点含有的子树的根节点称为该节点的子节点。上图中 D 节点、E 节点是 B 节点的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。上图中 D 节点、E 节点的共同父节点是 B 节点,故 D 和 E 为兄弟节点。
- 叶子节点:没有子节点的节点。上图中的 D、F、H、I 都是叶子节点。
- 节点的高度:该节点到叶子节点的最长路径所包含的边数。
- 节点的深度:根节点到该节点的路径所包含的边数
- 节点的层数:节点的深度+1。
- 树的高度:根节点的高度。
二叉树的分类
普通二叉树
二叉树是指每个节点最多只有两个分支的树。二个分支通常被称为“左子树”或“右子树”。并且,二叉树的分支具有左右次序,不能随意颠倒。
二叉树的第 i 层至多拥有 2^(i-1) 个节点,深度为 k 的二叉树至多总共有 2^(k+1)-1 个节点,至少有 2^(k) 个节点。
满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 K,且结点总数是(2^k) -1 ,则它就是满二叉树。如下图所示:

完全二叉树
除最后一层外,若其余层都是满的,并且最后一层要不然是满的,要不然就是在右边缺少连续若干节点,则这个二叉树就是完全二叉树 。
大家可以想象为一棵树从根结点开始扩展,扩展完左子节点才能开始扩展右子节点,每扩展完一层,才能继续扩展下一层。如下图所示:

平衡二叉树
平衡二叉树 是一棵二叉排序树,且具有以下性质:
-
可以是一棵空树
-
如果不是空树,它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。

二叉树的存储
二叉树的存储主要分为 链式存储 和 顺序存储 两种:
链式存储
和链表类似,二叉树的链式存储依靠指针将各个节点串联起来,不需要连续的存储空间。每个节点包括三个属性:
-
数据 data。data 不一定是单一的数据,根据不同情况,可以是多个具有不同类型的数据。
-
左节点指针 left
-
右节点指针 right。

顺序存储
顺序存储就是利用数组进行存储,数组中的每一个位置仅存储节点的 data,不存储左右子节点的指针,子节点的索引通过数组下标完成。根结点的序号为 1,对于每个节点 Node,假设它存储在数组中下标为 i 的位置,那么它的左子节点就存储在 2i 的位置,它的右子节点存储在下标为 2i+1 的位置。
一棵完全二叉树的数组顺序存储如下图所示:

可以看到,如果我们要存储的二叉树不是完全二叉树,在数组中就会出现空隙,导致内存利用率降低。
二叉树的遍历
先序遍历

二叉树的先序遍历,就是先输出根结点,再遍历左子树,最后遍历右子树,遍历左子树和右子树的时候,同样遵循先序遍历的规则,也就是说,我们可以递归实现先序遍历。
代码如下:
public void preOrder(TreeNode root){if(root == null){return;}system.out.println(root.data);preOrder(root.left);preOrder(root.right);
}
中序遍历

二叉树的中序遍历,就是先递归中序遍历左子树,再输出根结点的值,再递归中序遍历右子树。
代码如下:
public void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);system.out.println(root.data);inOrder(root.right);
}
后序遍历
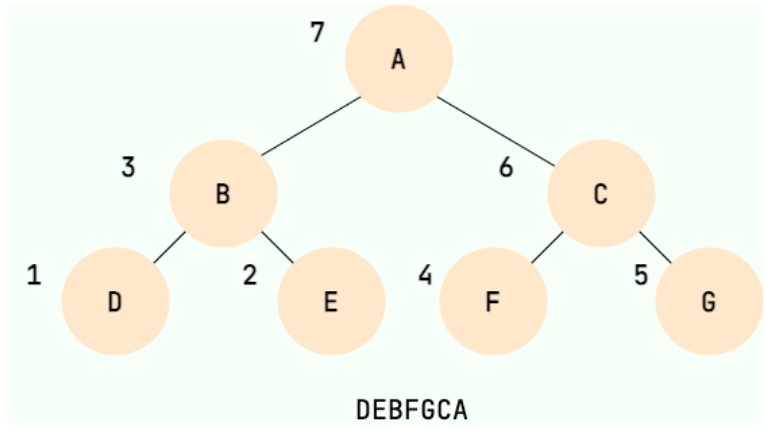
二叉树的后序遍历,就是先递归后序遍历左子树,再递归后序遍历右子树,最后输出根结点的值
代码如下:
public void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);system.out.println(root.data);
}