PHP 插值搜索（Interpolation Search）

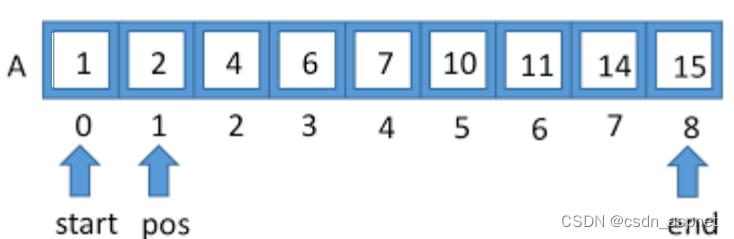
给定一个由 n 个均匀分布值 arr[] 组成的排序数组，编写一个函数来搜索数组中的特定元素 x。
线性搜索需要 O(n) 时间找到元素，跳转搜索需要 O(? n) 时间，二分搜索需要 O(log n) 时间。插值搜索是对实例二分搜索的改进，其中排序数组中的值是均匀分布的。

插值在一组离散的已知数据点的范围内构造新的数据点。二分查找总是到中间元素去检查。

另一方面，插值搜索可以根据正在搜索的键的值去不同的位置。例如，如果键的值更接近最后一个元素，则插值搜索很可能从末尾侧开始搜索。为了找到要搜索的位置，它使用以下公式。

// 公式的思想是
当要搜索的元素更接近arr[hi]时，返回较高的pos值。
// 当接近 arr[lo] 时值更小
arr[] ==> 需要查找元素的数组
x ==> 要搜索的元素
lo ==> arr[] 中的起始索引
hi ==> arr[] 中的结束索引

        有许多不同的插值方法，其中一种称为线性插值。线性插值采用两个数据点，我们假设为 (x1,y1) 和 (x2,y2)，公式为：在点 (x,y) 处。
        该算法的工作原理类似于我们在字典中搜索单词。插值搜索算法改进了二分搜索算法。查找值的公式为：K = 数据-低/高-低。
        K是一个常数，用于缩小搜索空间。在二分查找的情况下，该常数的值为：K=(low+high)/2。

pos 的公式可以推导如下：
我们假设数组的元素是线性分布的，直线的一般方程：y = m*x + c，y 是数组中的值，x 是其索引。
现在将 lo、hi 和 x 的值代入方程：
arr[hi] = m*hi+c ----(1)
arr[lo] = m*lo+c ----(2)
x = m* pos + c ----(3)
m = (arr[hi] - arr[lo] )/ (hi - lo)
从 (3) x - arr[lo] = m * (pos - lo) 减去 eqxn (2) lo)
lo + (x - arr[lo])/m = pos
pos = lo + (x - arr[lo]) *(hi - lo)/(arr[hi] - arr[lo])

算法
除了上面的划分逻辑之外，插值算法的其余部分是相同的。
        步骤1：在循环中，使用探针位置公式计算“pos”的值。
        步骤2：如果匹配，则返回该项的索引，并退出。
        步骤3：如果该项小于arr[pos]，则计算左子数组的探针位置。否则，在右侧子数组中计算相同的值。
        步骤4：重复直到找到匹配项或子数组减少到零。

下面是算法的实现：

<?php
// PHP program to implement $erpolation search
// with recursion

// If x is present in arr[0..n-1], then returns
// index of it, else returns -1.
function interpolationSearch($arr, $lo, $hi, $x)
{
// Since array is sorted, an element present
// in array must be in range defined by corner
if ($lo <= $hi && $x >= $arr[$lo] && $x <= $arr[$hi]) {
// Probing the position with keeping
// uniform distribution in mind.
$pos = (int)($lo
+ (((double)($hi - $lo)
/ ($arr[$hi] - $arr[$lo]))
* ($x - $arr[$lo])));

// Condition of target found
if ($arr[$pos] == $x)
return $pos;

// If x is larger, x is in right sub array
if ($arr[$pos] < $x)
return interpolationSearch($arr, $pos + 1, $hi,
$x);

// If x is smaller, x is in left sub array
if ($arr[$pos] > $x)
return interpolationSearch($arr, $lo, $pos - 1,
$x);
}
return -1;
}

// Driver Code
// Array of items on which search will
// be conducted.
$arr = array(10, 12, 13, 16, 18, 19, 20, 21, 22, 23, 24, 33,
35, 42, 47);
$n = sizeof($arr);

$x = 47; // Element to be searched
$index = interpolationSearch($arr, 0, $n - 1, $x);

// If element was found
if ($index != -1)
echo "Element found at index ".$index;
else
echo "Element not found.";
return 0;
#This code is contributed by Susobhan Akhuli
?>