文章目录
前言
1、回归和分类的本质
(1)回归(Regression)的本质
(2)分类(Classification)的本质
2、回归和分类的原理
(1)回归(Regression)的原理
(2)分类(Classification)的原理
3、回归和分类的算法
(1)回归(Regression)的算法
(2)分类(Classification)的算法
前言
本文将从回归和分类的本质、回归和分类的原理、回归和分类的算法三个方面,详细介绍回归和分类 (Regression And Classification)。
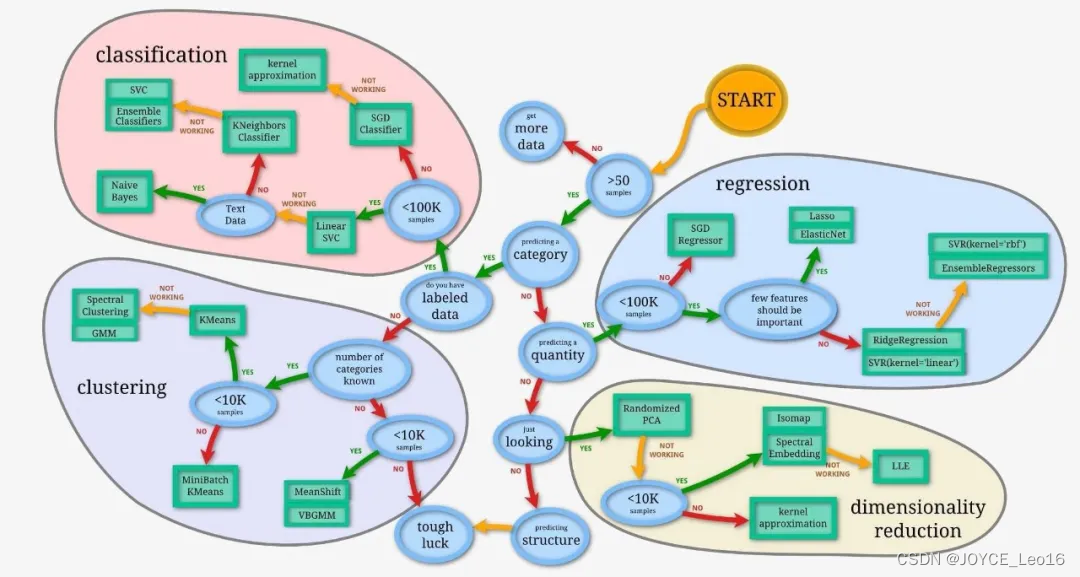
1、回归和分类的本质
回归和分类是机器学习中两种基本的预测方法,它们的本质区别在于输出变量的类型。回归问题输出的是连续的数值,分类问题输出的是有限的、离散的类别标签。两者都是监督学习的一部分,都依赖于带有标签的训练数据来学习模型。
(1)回归(Regression)的本质
回归的目的是预测数值型的目标值,本质是寻找自变量和因变量之间的关系,以便能够预测新的、未知的数据点的输出值。例如,根据房屋的面积、位置等特征预测其价格(房价预测、股票价价格预测、温度预测等)。
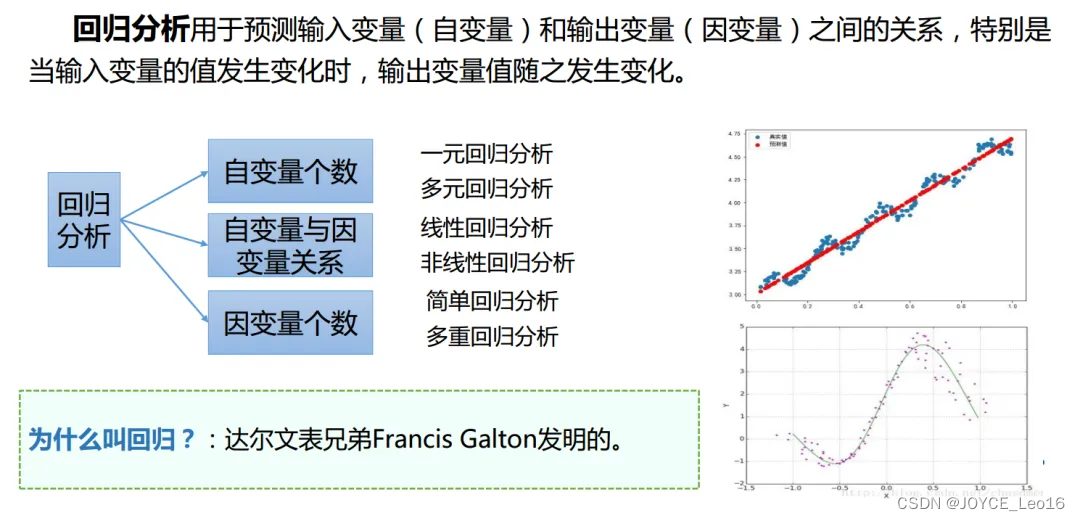
回归的本质
- 自变量个数:
一元回归:只涉及一个自变量和一个因变量的回归分析。
多元回归:涉及两个或更多个自变量和一个因变量的回归分析。
- 自变量与因变量的关系:
线性回归:自变量与因变量之间的关系被假定为线性的,即因变量是自变量的线性组合。
非线性回归:自变量与因变量之间的关系是非线性的,这通常需要通过非线性模型来描述。
- 因变量个数:
简单回归:只有一个因变量的回归分析,无论自变量的数量如何。
多重回归:涉及多个因变量的回归分析。在这种情况下,模型试图同时预测多个因变量的值。
(2)分类(Classification)的本质
分类的目的是预测标签型的目标值,本质是根据输入数据的特征将其划分到预定义的类别中。例如,根据图片的内容判断其所属的类别(猫、狗、花等)(邮件是否为垃圾邮件、疾病诊断的患病与否)。

分类的本质
- 二分类(Binary Classification):
表示分类任务中有两个类别。在二分类中,我们通常使用一些常见的算法来进行分类,如逻辑回归、支持向量机等。例如,我们想要识别一些图片是不是猫,这就是一个二分类问题,因为答案只有是或不是两种可能。
- 多分类(Multi-Class Classification):
表示分类任务中有多个类别。多分类是假设每个样本都被设置了一个且仅有一个标签:一个水果可以是苹果或者梨,但是同时不可能是两者。在多分类中,我们可以使用一些常见的算法来进行分类,如决策树、随机森林等。例如,对一堆水果图片进行分类,它们可能是橘子、苹果、梨等,这就是一个多分类问题。
- 多标签分类(Multi-Label Classification):
给每个样本一系列的目标标签,可以想象成一个数据点的各属性不是相互排斥的。多标签分类的方法分为两种,一种是将问题转化为传统的分类问题,二是调整现有的算法来适应多标签的分类。例如,一个文本可能被同时认为是宗教、政治、金融或者教育相关的话题,这就是一个多标签分类问题,因为一个文本可以同时有多个标签。
2、回归和分类的原理
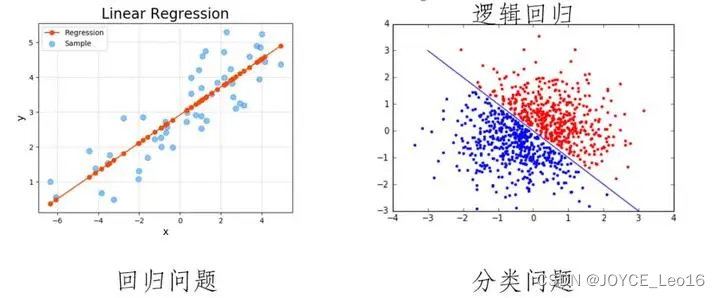
线性回归 vs 逻辑回归
(1)回归(Regression)的原理
通过建立自变量和因变量之间的数字模型来探究它们之间的关系。
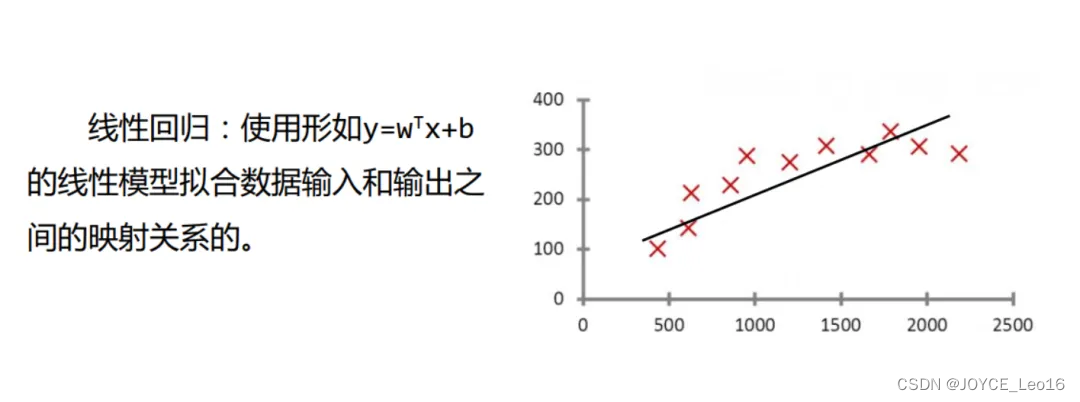
线性回归
线性回归(Linear Regression):求解权重(w)和偏置(b)的主要步骤。
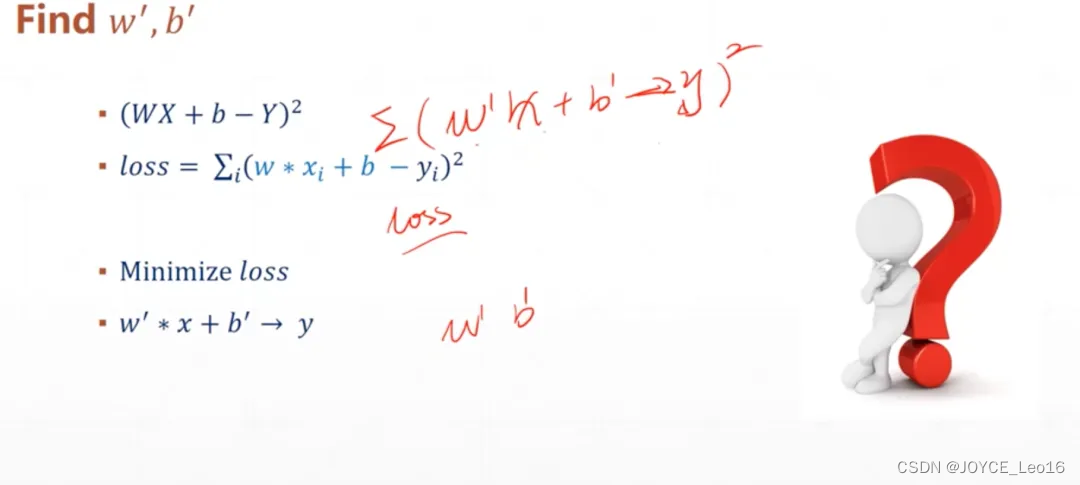
求解权重(w)和偏置(b)
- 初始化权重和偏置:为权重
和偏置
选择初始值,并准备训练数据
和标签
。
- 定义损失函数:选择一个损失函数(如均方误差)来衡量模型预测与实际值之间的差距。
- 应用梯度下降算法:使用梯度下降算法迭代更新
和
,以最小化损失函数,直到满足停止条件。
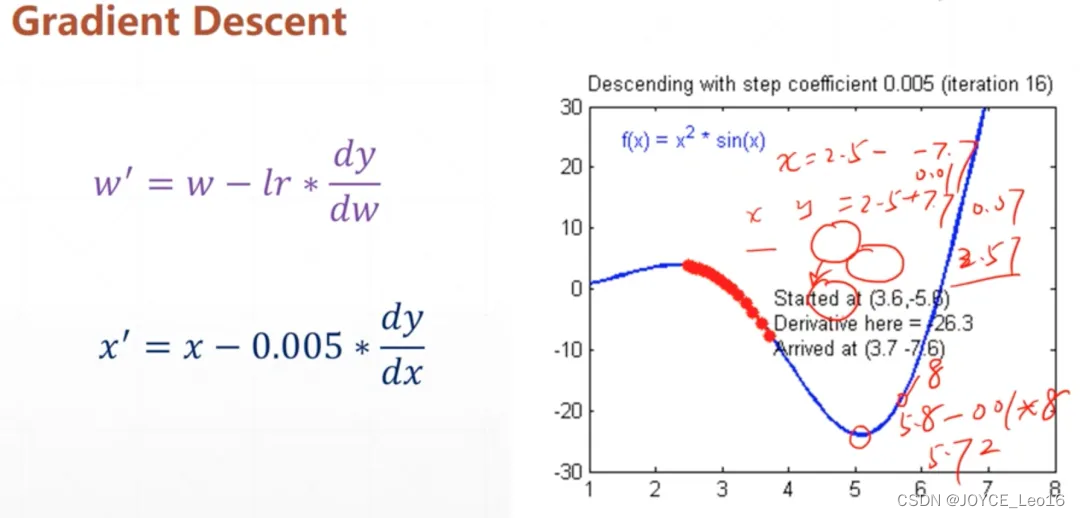
梯度下降算法迭代更新 w 和 b
- 获取并验证最终参数:当算法收敛时,得到
和
,并在验证集上检查模型性能。
- 构建最终模型:使用最终的
和
构建线性回归模型,用于新数据预测。
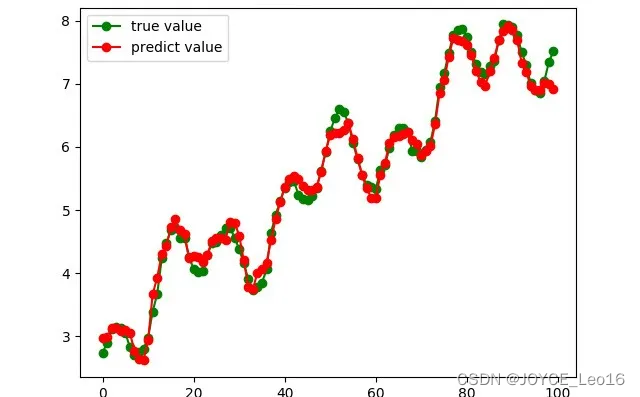
新数据预测
(2)分类(Classification)的原理
根据事物或概念的共同特征将其划分为同一类别,而将具有不同特征的事物或概念划分为不同类别。
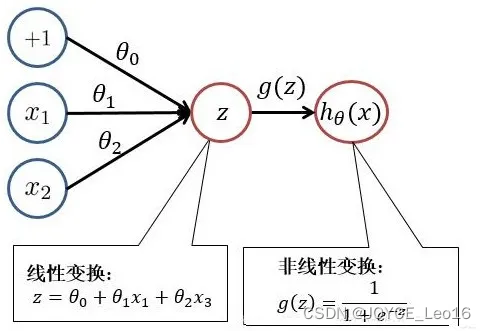
逻辑回归
逻辑回归(Logistic Regression):通过sigmoid函数将线性回归结果映射为概率的二分类算法。
- 特征工程:转换和增强原始特征以更好地表示问题。
- 模型建立:构建逻辑回归模型,使用sigmoid函数将线性组合映射为概率。
- 模型训练:通过优化算法(如梯度下降)最小化损失函数来训练模型。
- 模型评估:使用验证集或测试集评估模型的性能。
- 预测:应用训练好的模型对新数据进行分类预测。
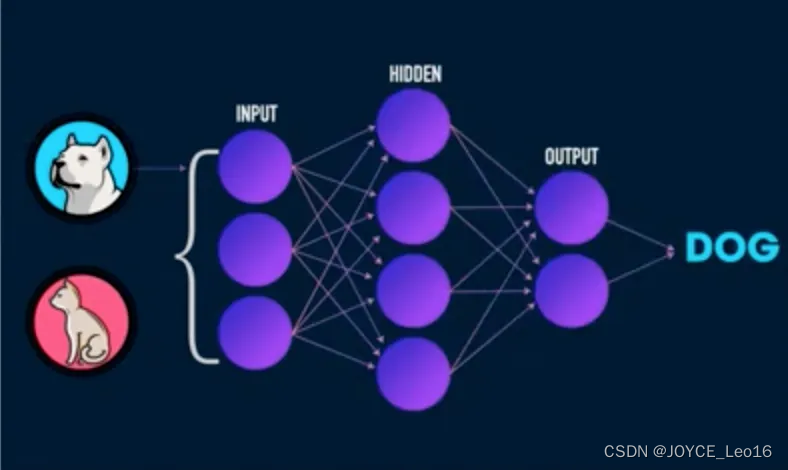
猫狗识别
3、回归和分类的算法
(1)回归(Regression)的算法
主要用于预测数值型数据。
- 线性回归(Linear Regression):这是最基本和常见的回归算法,它假设因变量和自变量之间存在线性关系,并通过最小化预测值和实际值之间的平方差来拟合数据。
- 多项式回归(Polynomial Regression):当自变量和因变量之间的关系是线性的,可以使用多项式回归。它通过引入自变量的高次项来拟合数据,从而捕捉非线性关系。
- 决策树回归(Decision Tree Regression):决策树回归是一种基于树结构的回归方法,它通过构建决策树来划分数据空间,并在每个叶节点上拟合一个简单的模型(如常数或线性模型)。决策树回归易于理解和解释,能够处理非线性关系,并且对特征选择不敏感。
- 随机森林回归(Random Forest Regression):随机森林回归是一种集成学习方法,它通过构建多个决策树并将它们的预测结果组合起来来提高回归性能。随机森林回归能够处理高维数据和非线性关系,并且对噪声和异常值具有一定的鲁棒性。
(2)分类(Classification)的算法
主要用于发现类别规则并预测新数据的类别。
- 逻辑回归(Logistic Regression):尽管名字中有“回归”,但实际上逻辑回归是一种分类算法,常用于二分类问题。它通过逻辑函数将线性回归的输出映射到(0,1)之间,得到样本点属于某一类别的概率。在回归问题中,有时也使用逻辑回归来处理因变量是二元的情况,此时可以将问题看作是对概率的回归。
- 支持向量机(SVM):支持向量机是一种基于统计学习理论的分类算法。它通过寻找一个超平面来最大化不同类别之间的间隔,从而实现分类。SVM在高维空间和有限样本情况下表现出色,并且对于非线性问题也可以使用核函数进行扩展。
- K最近邻(KNN):K最近邻是一种基于实例的学习算法,它根据输入样本的K个最近邻样本的类别来确定输入样本的类别。KNN算法简单且无需训练阶段,但在处理大规模数据集时可能效率较低。
- 朴素贝叶斯分类器:朴素贝叶斯是一种基于贝叶斯定理的分类算法,它假设特征之间相互独立(即朴素假设)。尽管这个假设在实际应用中往往不成立,但朴素贝叶斯分类器在许多领域仍然表现出色,尤其是在文本分类和垃圾邮件过滤等方面。
参考:架构师带你玩转AI