位运算（均是拷贝运算，不会影响原数据，这点要注意）

&、|、^

位运算特性+细节

首先，我们尝试不使用递归来解决这道题，他让我们判断是一个数是否为2的次幂。
尝试往位运算方面靠，位运算是通过二进制来解决问题的，而二进制就是2的次幂的表示，且，二进制从低位向高位，依次是2的012345…次方，所以，我们可以知道二进制表示为10000的数，（即第一位是1，后面全是0的数）是2的次幂数
所以，初步的认知已经建立了。之后寻找位运算的特性，如果一个数是1000的话，那么0111 + 1 就是 1000，而1000与0111做位与运算，可以得到0000，所以可以通过该性质找到10000特点的数

注意点1：小于等于0的数，可以直接排除
注意点2：进行位运算时，要在做完位运算之后，加一层括号，因为位运算的优先级低于==

知识补充

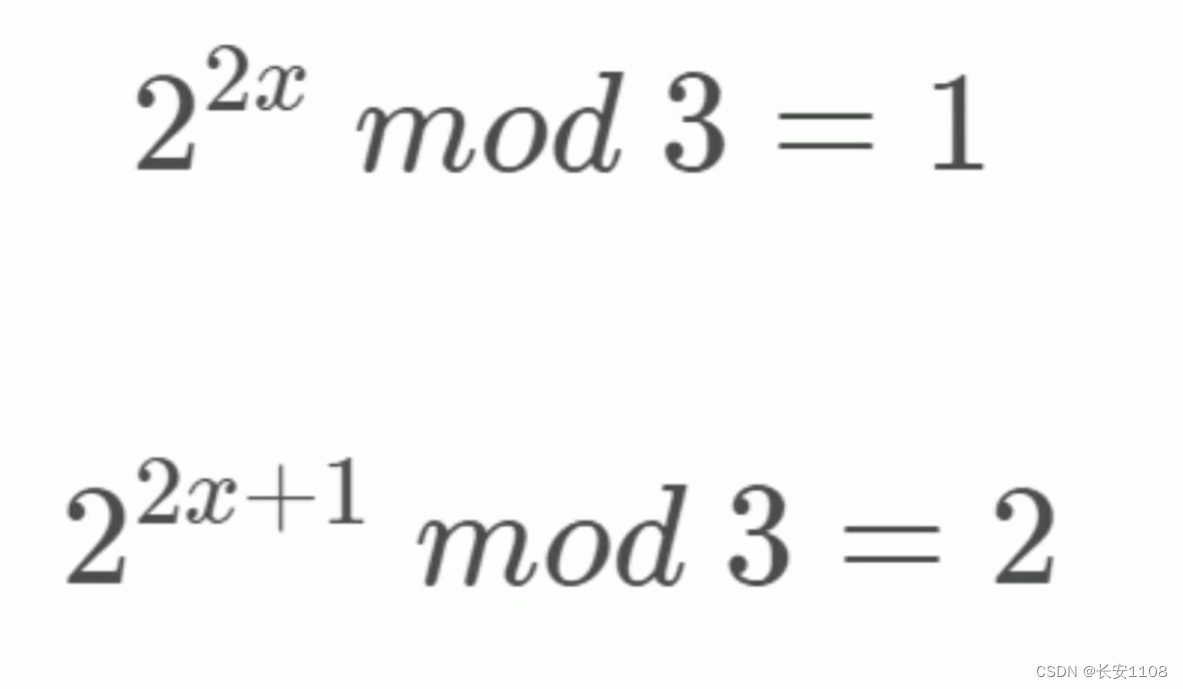
2的偶数次幂mod3等于1，例如4、16等，mod3 等于 1
而2的奇数次幂，就是2的偶数次幂再乘2，此时如8、32，mod3等于2

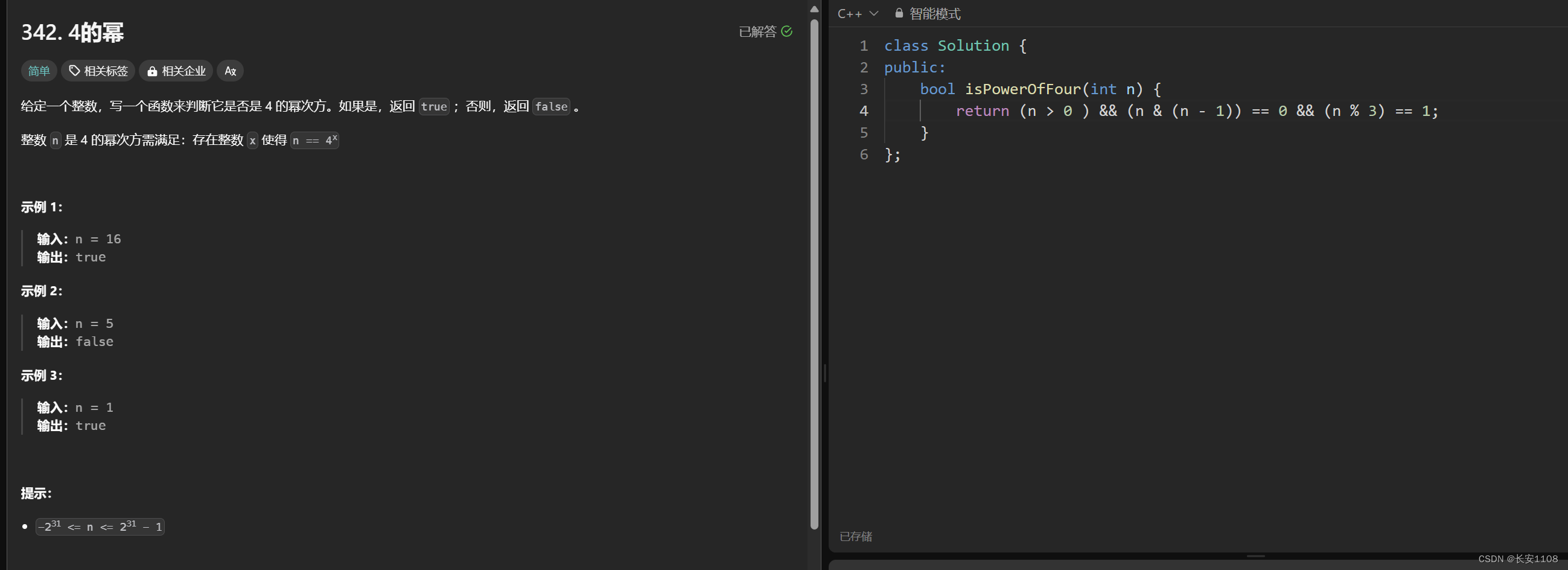
所以在求4的次幂时，因为2的偶次幂，一定是4的次幂，所以，我们在找到2的次幂数的基础上，再找到那些是2的偶次幂的数，那些数mod3==1

对于n-1的理解

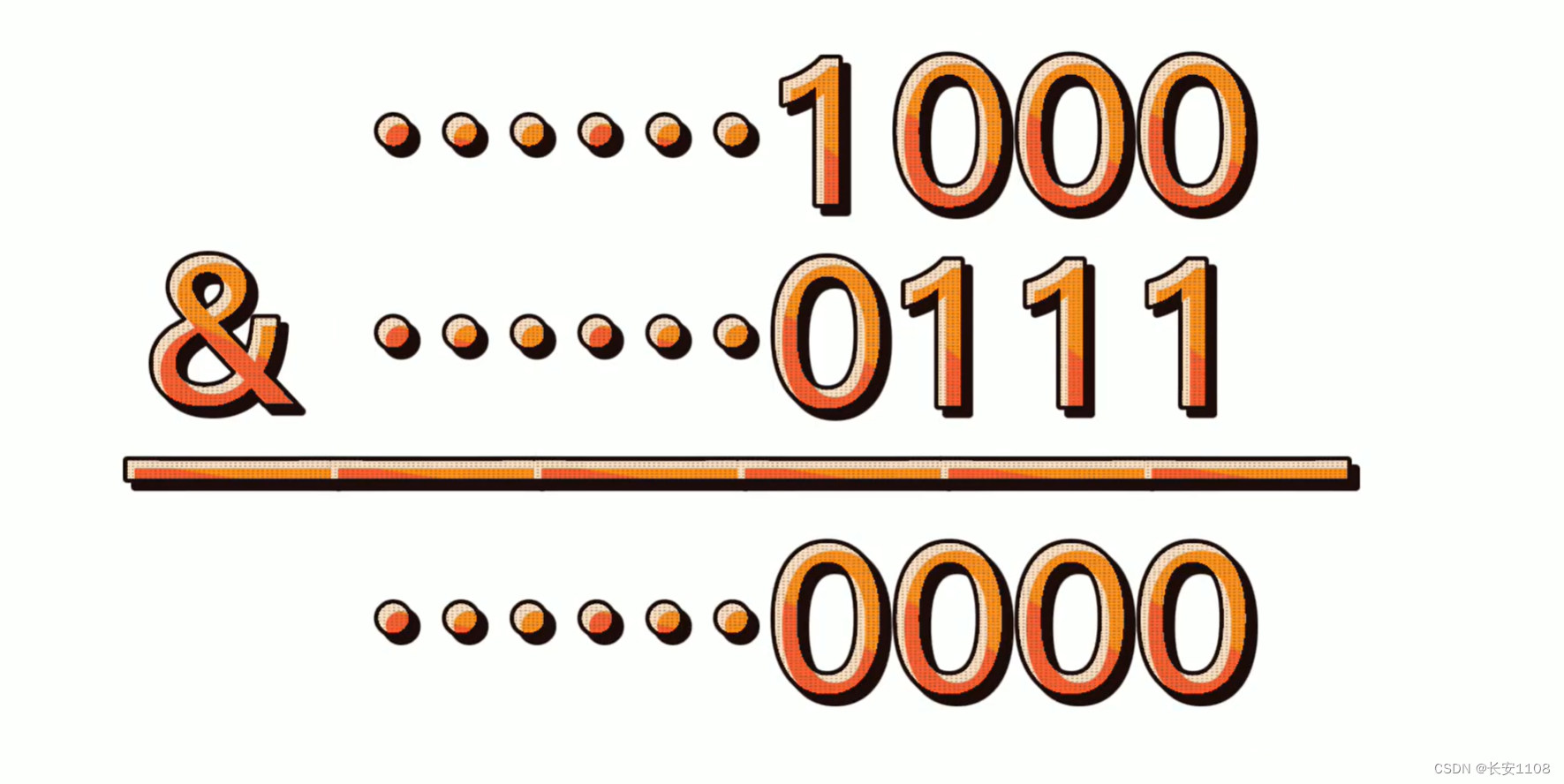
对于一个二进制 n = 10000010000101010，n - 1 = 10000010000101000，n - 1会将一个数的二进制表达最右边的1变为0，而其他不变，利用该特点可以得到1的个数

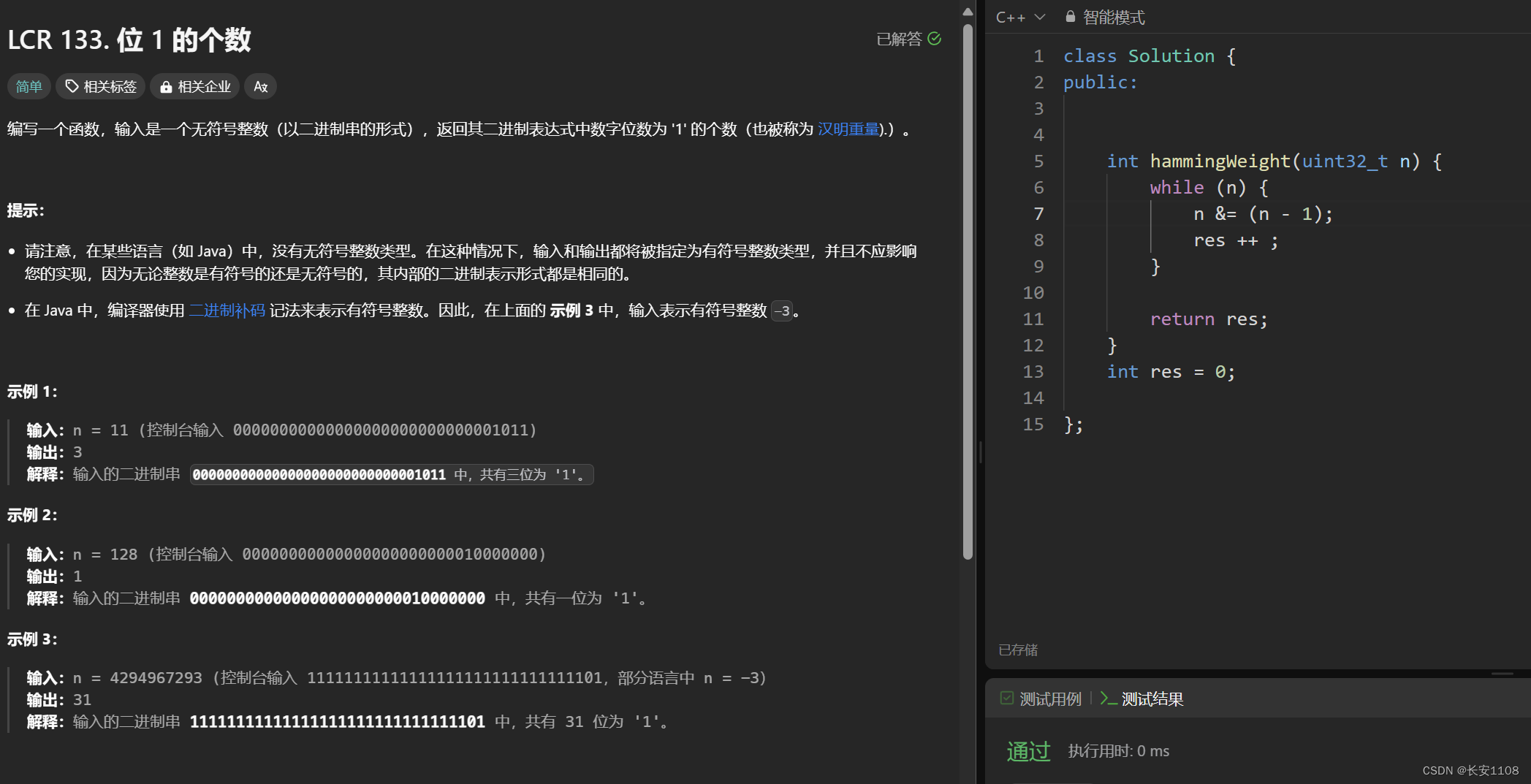
或者使用lowbit，见算法一栏“基础算法”（lowbit的时间复杂度更低）

异或来实现数字交换

首先，a = a ^ b，此后我们可以将一个a看成是变化之后的a，而如果a^b，则是原数据a、b
b = a ^ b，此时a是变化之后的a，将其拆开：a ^ b ^ b，此时a是变化之前的a，所以，就等于a ^ 0，最终等于原来的a
而到此时，a除了在第一行做出了改变，其他地方均无改变，所以，还是第一行的结论：可以将一个a看成是变化之后的a，而如果a^b，则是原数据a、b
所以，a = a ^ b，a是第一行代码执行后变化的a，b是原来的a，所以，将a拆开（得到原来的a 和 b）并且将b换成原来的a：a ^ b ^ a，再使用交换律，得到a ^ a ^ b，最后等于原来的b

找到只出现一次的数据，其余数据出现偶数次

首先定义res = 0；
之后将res与数组中的每个数进行异或运算
用到的知识点：
1、0^a = a
2、b^b = 0；

>> 、<<

二进制中相邻的位的特点

判断相邻位数是否交替为0、1

也就是相邻的位数上不能是相同的，即不能是00或者11，
而00对应于十进制是0，11对应于十进制是3

所以，如果 n&3 == 3，则表示当前n的右边两位是11
如果n&3 = = 0,则表示当前n的右边是00，（注意，此处还是&3，即00&11结果为00。逻辑上，他还有个等价式是00&00结果为11，也就是n&0 = = 3，但是如果&0的话，可能转为二进制就变成&一位0，而&3的话，铁定在二进制是&两位，所以，&0会导致某些数据点报错）

每次判断完之后，将n>>1右移一位，并覆盖到n，注意每次右移一位，如果右移两位，可能会出现0110，这样的数据，会出错

注意点1：&运算一次进行多位二进制判断时，尽量避免&0，尽可能找其等效式
注意点2：从此处我们也可以看出，我们之前的x&1，就是利用&的原始定义来求的，最终求出x二进制的个位，因为1表示成二进制就是…00001

找出某个排列的所有子集

我们以一个存有三个数的数组为例，那么nums.size()就等于3，而他的子集可能会是没有元素，或者一个元素，或者两个，或者三个，如果我们挨个遍历的话，时间复杂度肯定会剧增，所以，我们利用二进制，即利用位运算

我们可以将某个数在or不在，表示为二进制上的1or0，现在我们已经有了不同的子集与二进制的对应，那么如何进行遍历呢，我们可以让
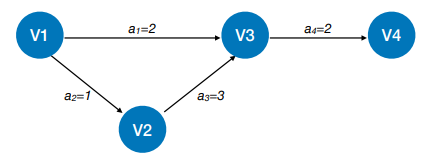
i 从 0 遍历到 小于（1 << size()），因为1左移size位，就变成了1000，他正好就是四位的第一个数，所以小于他的，就是所有0位1位2位3位的二进制，也就是下图所示情况。这样，每个 i 的二进制，都标识了一种数组子集的情况

有了这些 i 的循环，我们如何判断当前是哪个二进制位上为1呢，我们可以在每个i循环步内，定义一个 j 循环，j 从 0 到小于size，
他实际上数组下标，判断 i & （1 << j）是否为1，而（1 << j）的循环是 001、010、100，如果结果不为0，那么就是为1，即当前循环步的 i的二进制标识，与当前 j 二进制中为1的那一位，都是1，即表明，i 中对应 j 为1 的位置是1，则nums[ size - j - 1 ]就是当前子集的元素之一

但是注意，他的顺序不是“先是单个元素，然后两个，三个”，他会先输出两个单元素，再输出一个双元素，再输出一个单元素，…无规则的，因为3对应二进制11，肯定会得到两个数

如果想要从左边开始判断，适当修改 i 和 j 的循环方向

一级目录

二级目录

二级目录

二级目录

一级目录

二级目录

二级目录

二级目录

一级目录

二级目录

二级目录

二级目录

一级目录

二级目录

二级目录

二级目录