【洛谷】P9236 [蓝桥杯 2023 省 A] 异或和之和

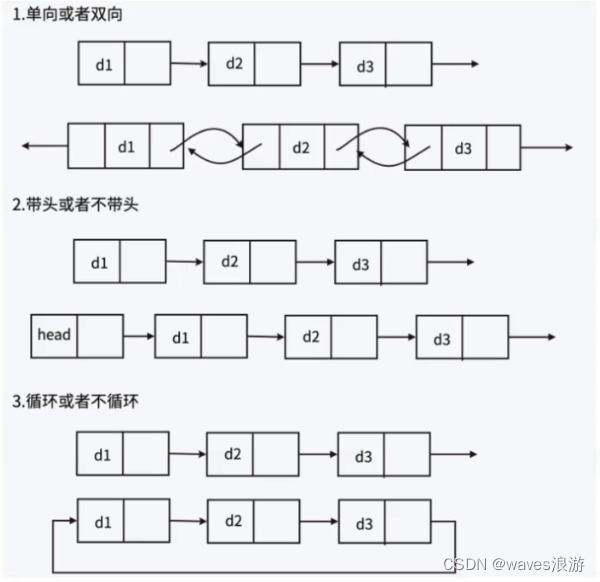
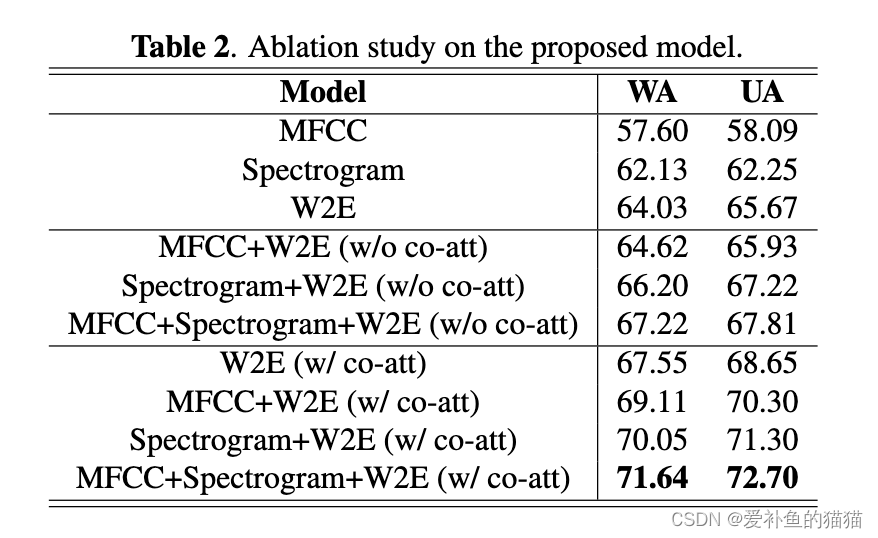
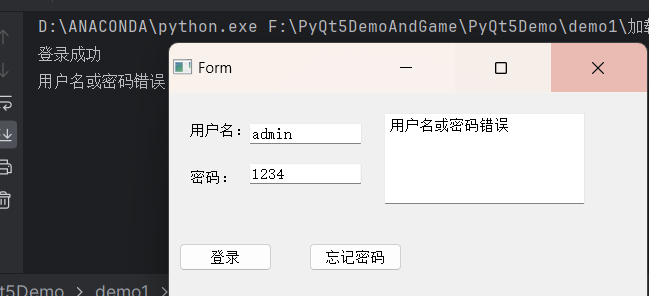
题目链接

P9236 [蓝桥杯 2023 省 A] 异或和之和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

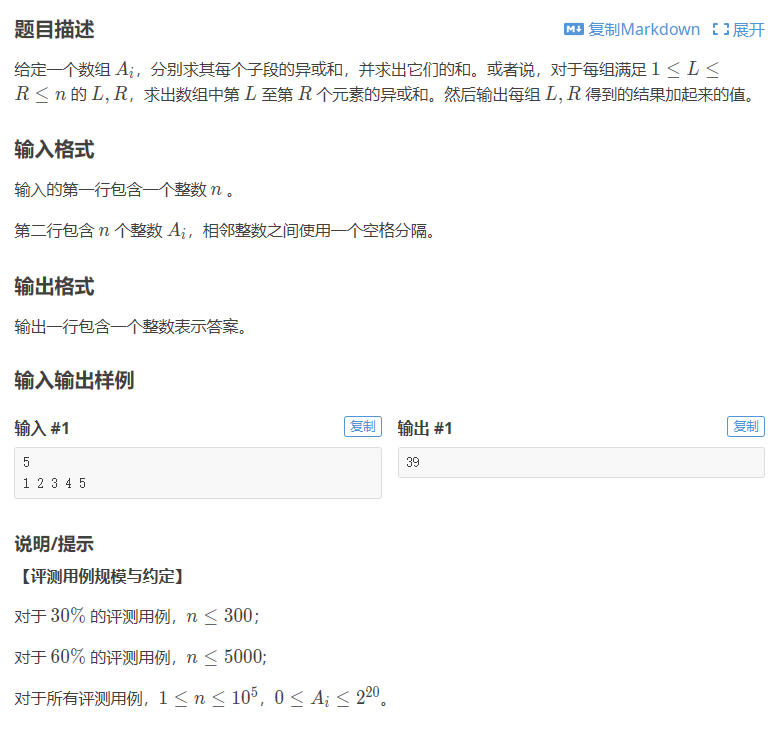
思路

1. 暴力求解

直接枚举出所有子数组，求每个子数组的异或和，再对所有的异或和求和

枚举所有子数组的时间复杂度为O（N^2），求每个子数组的异或和又要遍历一次数组，所以总的时间复杂度为O（N^3）

2. 优化

异或中有这么一个性质：a ^ b ^ b = a，即两个相同元素异或后为0，此性质推广到子数组同理

因此我们可以用前缀和的思想来快速得出一个区间的异或和。

此时可以将时间复杂度优化为O（N^2）

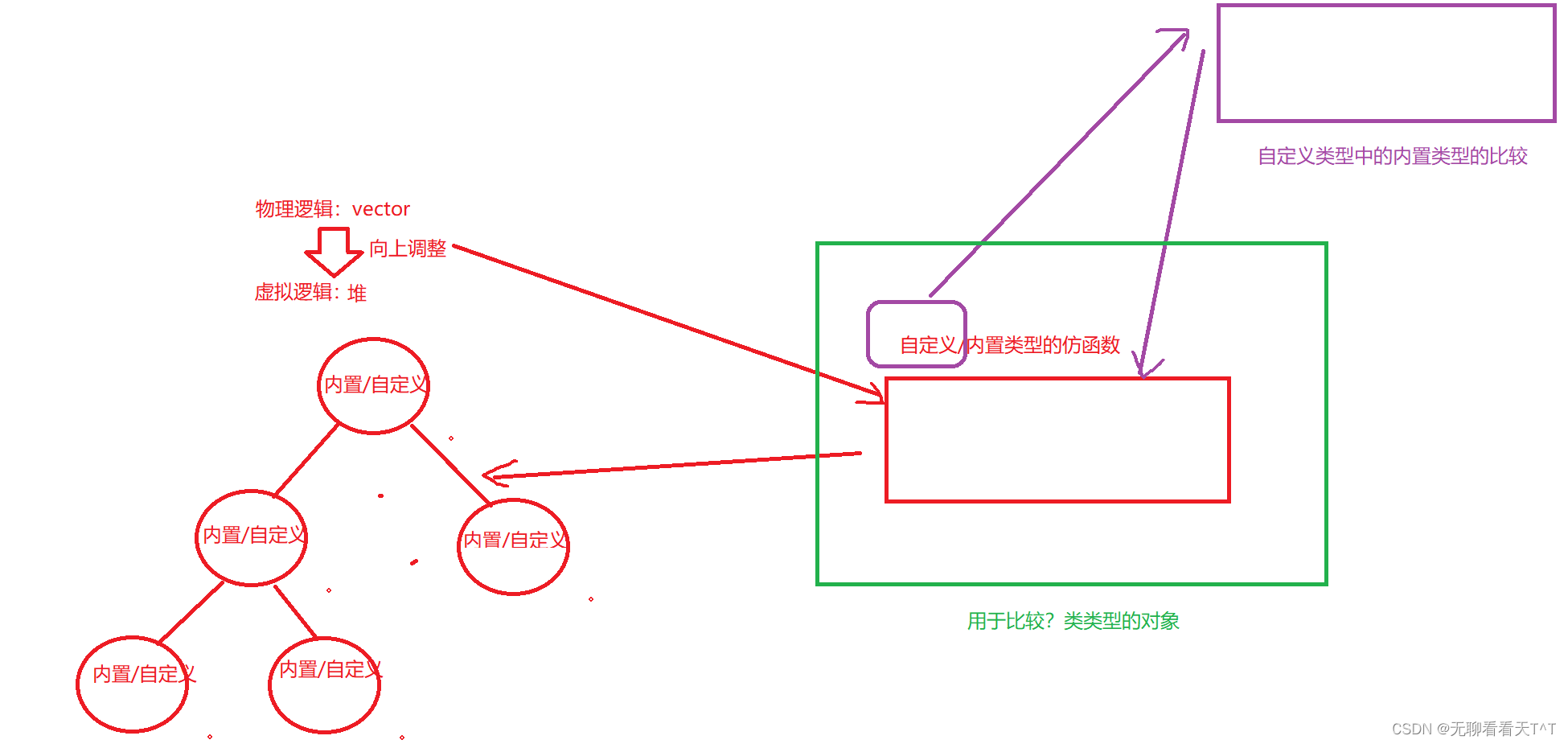
基于前缀和，我们进行进一步的优化：拆位法和贡献法

（1）拆位法

拆位法：将一个数转换成二进制形式，并拆分成单独的二进制位来计算

二进制中除了0就是1，由于异或的性质，我们可以得出一个结论：对于二进制位中的第i位而言，如果这一位中1的个数为奇数，那么异或后的结果中这一位就是1，否则为0

例如：

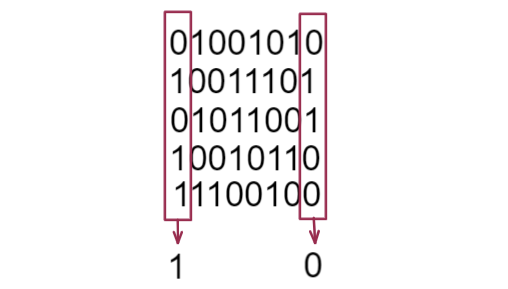
拆位法加上前缀和，我们就能计算出某个区间中这一位上1的个数，进而得出在该区间中这个二进制位异或后是0还是1

（2）贡献法

贡献法：从区间的角度转换成计算每个二进制位对答案的贡献

某个区间中，这一位异或后的结果为1时，这一位就产生了贡献；异或后的结果为0时这一位就不会产生贡献。

例如：

我们以一个二进制位作为一个计算周期，统计该位中1的前缀和

例如该位中1的前缀和为偶数，说明对于虚线内的这个区间，异或后该位为0，无贡献

注意：这里的区间最终异或后只可能为1或0，因此当我们谈论区间的贡献时，实际上也就是谈论该位是否有贡献

但是如果一个前缀和为偶数的区间减去一个前缀和为奇数的区间，所得到的新的区间的前缀和也为奇数，即新区间中该位异或后的结果为1，有贡献

例如：

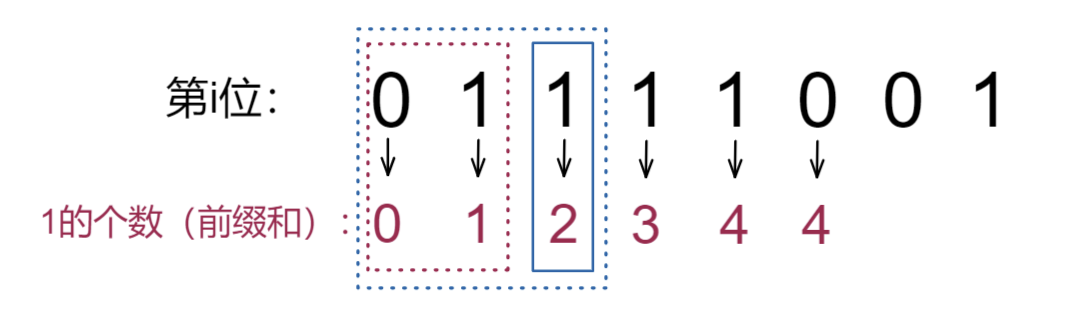
蓝色虚线的区间前缀和为偶数（2），减去红色虚线前缀和为奇数（1）的区间，所得到蓝色实线区间的1的前缀和为奇数（2 - 1 = 1），则该实线区间异或后也有贡献

通过观察，我们可以得出以下结论：

对于第i个二进制位，如果以第n个数为结尾的区间所对的前缀和为偶数时，该区间能够提供 前面奇数前缀和的个数 个贡献区间

例如对于上面蓝色虚线的区间，其前面有一个奇数前缀和，那么该区间自身就能提供一个贡献区间

而该位中1的前缀和为奇数，与上面同理，我们只需要计算出前面所有前缀和为偶数的区间个数，减去这些前缀和为偶数的区间得到的新区间，前缀和都为奇数（奇-偶=奇），则都有贡献

而因为该区间本身的前缀和为奇数，所以能够提供的贡献区间为：1 + 前面偶数前缀和的个数

通过提示我们可以知道所有的数中有效位数不会超过20

代码

#include <bits/stdc++.h>
using namespace std;
#define ll long longll n;int main()
{cin >> n;ll *arr = new ll[n];for (int i = 0; i < n; i++)cin >> arr[i];ll pow = 1, sum = 0;  for (int i = 0; i < 20; i++) //最多计算20个二进制位 {ll counti = 0, oddnum = 0, evenum = 0, range = 0; //counti统计1的前缀和，oddnum统计奇数前缀和的个数//evenum统计偶数前缀和的个数，range统计有贡献区间个数 for (int j = 0; j < n; j++) //遍历n个整数 {if (arr[j] & 1) //按位与1后结果为1，说明最低位为1，否则为0 counti++; //更新前缀和 if (counti % 2 == 1) //前缀和为奇数{range += 1 + evenum; //更新有贡献区间个数 oddnum++; //奇数前缀和的个数+1 }else //前缀和为偶数 {range += oddnum; //更新有贡献区间个数 evenum++; //偶数前缀和的个数+1 }arr[j] >>= 1; //移位 }sum += range * pow; //计算位数对结果的贡献值 pow *= 2; //更新pow }cout << sum;return 0;
}