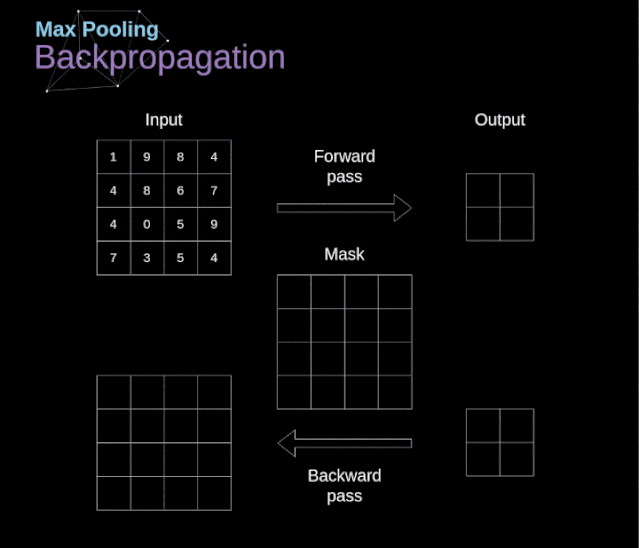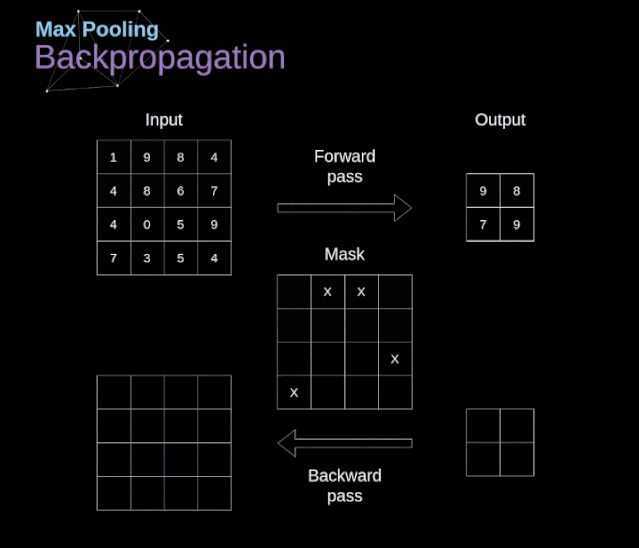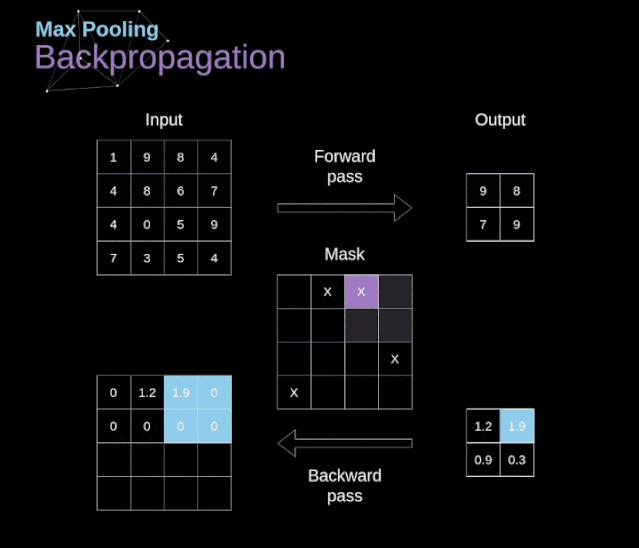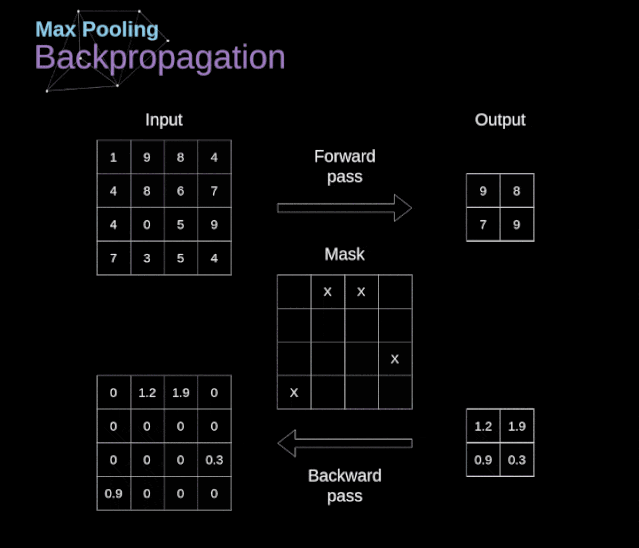
线性代数:构建数据的骨架
数学对象

标量(Scalar)
标量是最基本的数学对象,代表了单个的数值,无论是整数还是实数。在机器学习中,标量可以用来表示一个模型的单个参数,如偏差(bias)项。
向量(Vector)
向量是标量的直接扩展,表示由多个标量组成的有序集合。在数据科学中,一个实例或数据点的特征通常以向量的形式出现,其中每个元素代表一个特征。
矩阵(Matrix)
矩阵是二维数组,它扩展了向量的概念,允许我们同时操作多个数据点。在机器学习中,矩阵经常用于表示整个数据集,其中每行代表一个数据点,每列代表一种特征。
张量(Tensor)
张量是更高维度的数组,广泛应用于深度学习。例如,在处理图像数据时,一个彩色图像可以表示为一个3D张量,维度分别对应于图像的高度、宽度和颜色通道。
简单运算

矩阵转置(Matrix Transpose)
矩阵转置是将矩阵的行列互换的操作,是许多线性代数运算的基础。
矩阵求逆(Matrix Inversion)
矩阵求逆是找到一个矩阵,使得当它与原矩阵相乘时,结果为单位矩阵。矩阵求逆在理论上非常重要,尤其是在求解线性系统时。
矩阵乘法(Matrix Multiplication)
矩阵乘法是线性代数中最核心的运算之一,允许我们组合和转换数据集。它是定义线性变换的基础,也是深度学习中神经网络层之间传递信息的方式。
范数(Norm)
L_pLp 范数
L_pLp 范数是向量元素绝对值的p次方和的p次根。特别地,L_1L1 范数和L_2L2 范数在机器学习中广泛用于正则化,以避免过拟合。


概率论:不确定性的语言
随机变量

离散和连续
随机变量可以是离散的,取有限或可数无限多个值;或者是连续的,取值于某个区间内的所有实数。离散随机变量的例子包括掷硬币的结果,连续随机变量的例子包括测量的身高。

概率分布
PMF 和 PDF
离散随机变量的概率分布可以通过概率质量函数(PMF)描述,而连续随机变量的概率分布可以通过概率密度函数(PDF)描述。


边缘概率分布(Marginal Probability Distribution)

边缘概率描述了忽略其他变量后,单个随机变量的概率分布。
条件概率(Conditional Probability)

条件概率表示在给定一个事件发生的条件下,另一个事件发生的概率。
独立和条件独立

两个事件的独立意味着一个事件的发生不影响另一个事件的发生概率。条件独立则是在给定第三个事件的情况下,两个事件互不影响。
期望、方差和协方差
- **期望(Expectation)**表示随机变量的平均值。
-

- **方差(Variance)**衡量随机变量的波动大小。

- **协方差(Covariance)**衡量两个随机变量同时变化的趋势。
-

常见的概率分布
包括伯努利分布、二项分布、正态分布等,每种分布都有其特定的应用场景。



贝叶斯定理(Bayes' Theorem)

贝叶斯定理提供了一种在已知某些其他条件下,事件概率如何转换的方法。它是现代机器学习中不可或缺的工具,尤其在贝叶斯网络和贝叶斯推断中。
优化:寻找最佳解

梯度下降(Gradient Descent)

梯度下降是一种寻找函数最小值的方法,通过计算函数的梯度并沿着梯度的反方向更新参数来逐步逼近最小值点。
临界点(Critical Points)
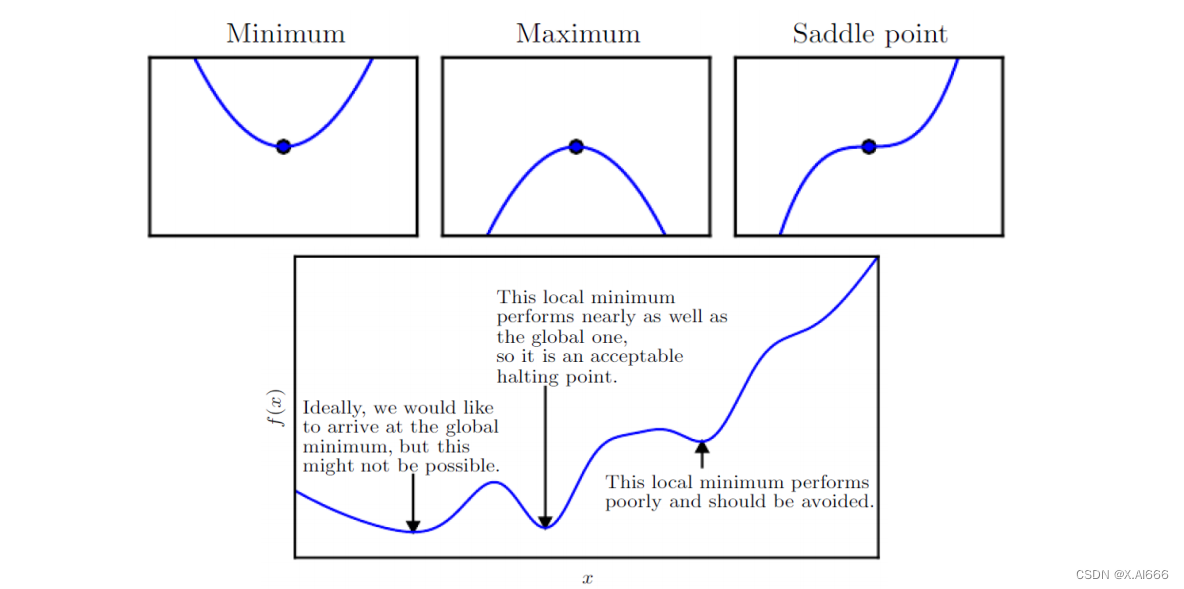
临界点是函数梯度为零的点,可以是局部最小值、局部最大值或鞍点。
微积分运算法则

微积分运算法则,包括链式法则、乘法法则和除法法则,是计算梯度下降法中梯度以及在更复杂优化问题中应用微积分的基础。
微积分运算法则在优化中的应用
微积分,特别是导数和偏导数,是理解和实施优化算法的基础。在机器学习中,我们通常需要最小化或最大化某个函数,例如损失函数或目标函数。要做到这一点,我们需要计算函数相对于其参数的梯度,即需要知道如何有效地应用微积分运算法则。

链式法则
链式法则是微积分中的一项关键法则,它允许我们计算复合函数的导数。在机器学习的背景下,这是反向传播算法的基础,后者是训练深度神经网络的主要方法。通过链式法则,我们可以将复杂模型的梯度分解为较简单函数梯度的乘积,从而有效地计算出梯度来更新模型参数。
乘法法则和除法法则
乘法法则和除法法则提供了计算两个函数相乘或相除的导数的方法。这在处理包含多个项相乘或相除的损失函数时非常有用。例如,在正则化项被添加到损失函数中时,可能需要应用这些法则来正确计算梯度。
优化技术的进阶主题
机器学习中的优化不仅仅局限于梯度下降和其变体。存在一系列高级技术,可以帮助更有效地解决优化问题。
动量和自适应学习率方法
动量方法借鉴了物理学中的概念,通过考虑之前梯度的累积来加速学习。自适应学习率方法(如Adam和RMSprop)则通过自动调整学习率来解决梯度下降中的一些常见问题,如学习率选择和梯度消失。
临界点的辨识与处理
识别函数的临界点是优化中的一个重要方面。在实践中,我们需要区分这些临界点是局部最小值、局部最大值还是鞍点,并采取策略避免陷入次优解。高级优化技术,如二阶方法,可以提供关于临界点性质的更多信息,但计算成本也更高。
结合理论与实践
机器学习中的优化是一个动态平衡的过程,涉及理论知识和实践技能的结合。理解线性代数、概率论和微积分的基础原理是构建有效模型的关键。同时,掌握各种优化技术和算法,能够让我们在实际问题中找到最佳解。
优化不仅仅是找到任何解,而是要找到在给定数据和约束条件下的最佳解。这要求我们深入理解模型的工作原理,以及如何通过优化算法调整模型参数以达到最佳性能。
在不断发展的机器学习领域,新的理论和技术不断涌现。保持对基础数学原理的坚实理解,同时紧跟最新的研究和技术发展,是每一个机器学习从业者和研究者的必备素质。
通过上述讨论,我们深入探讨了线性代数、概率论和优化这三个机器学习的核心数学基础,以及它们如何相互作用来支持和推动机器学习模型的开发和优化。理解这些概念为在这一激动人心的领域内进行创新和实践提供了坚实的基础。