政安晨：【Keras机器学习实践要点】（二十五）—— 使用 EANet（外部注意力转换器）进行图像分类

简介

设置

准备数据

配置超参数

使用数据增强

实施补丁提取和编码层

实施外部关注模块

实施 MLP 模块

执行变压器模块

实施 EANet 模式

培训 CIFAR-100

政安晨的个人主页：政安晨

欢迎 👍点赞✍评论⭐收藏

收录专栏: TensorFlow与Keras机器学习实战

希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正！

本文目标：利用外部注意力的变形器进行图像分类。

简介

本例实现了用于图像分类的 EANet 模型，并在 CIFAR-100 数据集上进行了演示。

EANet 引入了一种名为 "外部注意 "的新型注意机制，它基于两个外部、小型、可学习和共享的记忆，只需使用两个级联线性层和两个归一化层即可轻松实现。

它可以方便地取代现有架构中使用的自我注意。外部注意力具有线性复杂性，因为它只隐含地考虑了所有样本之间的相关性。

设置

import keras
from keras import layers
from keras import opsimport matplotlib.pyplot as plt

准备数据

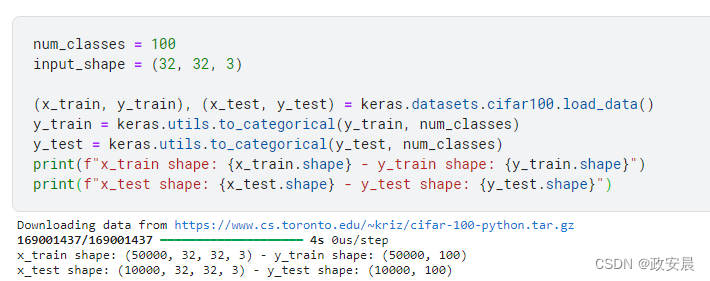
num_classes = 100
input_shape = (32, 32, 3)(x_train, y_train), (x_test, y_test) = keras.datasets.cifar100.load_data()
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")

演绎展示：

配置超参数

weight_decay = 0.0001
learning_rate = 0.001
label_smoothing = 0.1
validation_split = 0.2
batch_size = 128
num_epochs = 50
patch_size = 2  # Size of the patches to be extracted from the input images.
num_patches = (input_shape[0] // patch_size) ** 2  # Number of patch
embedding_dim = 64  # Number of hidden units.
mlp_dim = 64
dim_coefficient = 4
num_heads = 4
attention_dropout = 0.2
projection_dropout = 0.2
num_transformer_blocks = 8  # Number of repetitions of the transformer layerprint(f"Patch size: {patch_size} X {patch_size} = {patch_size ** 2} ")
print(f"Patches per image: {num_patches}")

结果演绎：

使用数据增强

data_augmentation = keras.Sequential([layers.Normalization(),layers.RandomFlip("horizontal"),layers.RandomRotation(factor=0.1),layers.RandomContrast(factor=0.1),layers.RandomZoom(height_factor=0.2, width_factor=0.2),],name="data_augmentation",
)
# Compute the mean and the variance of the training data for normalization.
data_augmentation.layers[0].adapt(x_train)

实施补丁提取和编码层

class PatchExtract(layers.Layer):def __init__(self, patch_size, **kwargs):super().__init__(**kwargs)self.patch_size = patch_sizedef call(self, x):B, C = ops.shape(x)[0], ops.shape(x)[-1]x = ops.image.extract_patches(x, self.patch_size)x = ops.reshape(x, (B, -1, self.patch_size * self.patch_size * C))return xclass PatchEmbedding(layers.Layer):def __init__(self, num_patch, embed_dim, **kwargs):super().__init__(**kwargs)self.num_patch = num_patchself.proj = layers.Dense(embed_dim)self.pos_embed = layers.Embedding(input_dim=num_patch, output_dim=embed_dim)def call(self, patch):pos = ops.arange(start=0, stop=self.num_patch, step=1)return self.proj(patch) + self.pos_embed(pos)

实施外部关注模块

def external_attention(x,dim,num_heads,dim_coefficient=4,attention_dropout=0,projection_dropout=0,
):_, num_patch, channel = x.shapeassert dim % num_heads == 0num_heads = num_heads * dim_coefficientx = layers.Dense(dim * dim_coefficient)(x)# create tensor [batch_size, num_patches, num_heads, dim*dim_coefficient//num_heads]x = ops.reshape(x, (-1, num_patch, num_heads, dim * dim_coefficient // num_heads))x = ops.transpose(x, axes=[0, 2, 1, 3])# a linear layer M_kattn = layers.Dense(dim // dim_coefficient)(x)# normalize attention mapattn = layers.Softmax(axis=2)(attn)# dobule-normalizationattn = layers.Lambda(lambda attn: ops.divide(attn,ops.convert_to_tensor(1e-9) + ops.sum(attn, axis=-1, keepdims=True),))(attn)attn = layers.Dropout(attention_dropout)(attn)# a linear layer M_vx = layers.Dense(dim * dim_coefficient // num_heads)(attn)x = ops.transpose(x, axes=[0, 2, 1, 3])x = ops.reshape(x, [-1, num_patch, dim * dim_coefficient])# a linear layer to project original dimx = layers.Dense(dim)(x)x = layers.Dropout(projection_dropout)(x)return x

实施 MLP 模块

def mlp(x, embedding_dim, mlp_dim, drop_rate=0.2):x = layers.Dense(mlp_dim, activation=ops.gelu)(x)x = layers.Dropout(drop_rate)(x)x = layers.Dense(embedding_dim)(x)x = layers.Dropout(drop_rate)(x)return x

执行变压器模块

def transformer_encoder(x,embedding_dim,mlp_dim,num_heads,dim_coefficient,attention_dropout,projection_dropout,attention_type="external_attention",
):residual_1 = xx = layers.LayerNormalization(epsilon=1e-5)(x)if attention_type == "external_attention":x = external_attention(x,embedding_dim,num_heads,dim_coefficient,attention_dropout,projection_dropout,)elif attention_type == "self_attention":x = layers.MultiHeadAttention(num_heads=num_heads,key_dim=embedding_dim,dropout=attention_dropout,)(x, x)x = layers.add([x, residual_1])residual_2 = xx = layers.LayerNormalization(epsilon=1e-5)(x)x = mlp(x, embedding_dim, mlp_dim)x = layers.add([x, residual_2])return x

实施 EANet 模式

EANet 模型利用了外部注意力。咱们发现，大多数像素只与其他几个像素密切相关，N 对 N 的注意力矩阵可能是多余的。

因此，他们提出了外部注意力模块作为替代方案，外部注意力的计算复杂度为 O（d * S * N）。由于 d 和 S 都是超参数，所提出的算法与像素数量呈线性关系。事实上，这等同于丢弃补丁操作，因为图像中的补丁所包含的很多信息都是冗余和不重要的。

def get_model(attention_type="external_attention"):inputs = layers.Input(shape=input_shape)# Image augmentx = data_augmentation(inputs)# Extract patches.x = PatchExtract(patch_size)(x)# Create patch embedding.x = PatchEmbedding(num_patches, embedding_dim)(x)# Create Transformer block.for _ in range(num_transformer_blocks):x = transformer_encoder(x,embedding_dim,mlp_dim,num_heads,dim_coefficient,attention_dropout,projection_dropout,attention_type,)x = layers.GlobalAveragePooling1D()(x)outputs = layers.Dense(num_classes, activation="softmax")(x)model = keras.Model(inputs=inputs, outputs=outputs)return model

培训 CIFAR-100

model = get_model(attention_type="external_attention")model.compile(loss=keras.losses.CategoricalCrossentropy(label_smoothing=label_smoothing),optimizer=keras.optimizers.AdamW(learning_rate=learning_rate, weight_decay=weight_decay),metrics=[keras.metrics.CategoricalAccuracy(name="accuracy"),keras.metrics.TopKCategoricalAccuracy(5, name="top-5-accuracy"),],
)history = model.fit(x_train,y_train,batch_size=batch_size,epochs=num_epochs,validation_split=validation_split,
)

演绎展示：

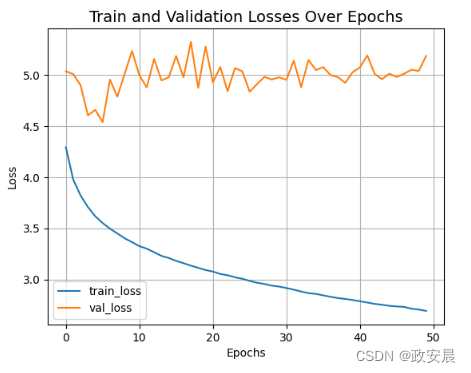
Epoch 1/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 88s 186ms/step - accuracy: 0.0398 - loss: 4.4477 - top-5-accuracy: 0.1500 - val_accuracy: 0.0616 - val_loss: 5.0341 - val_top-5-accuracy: 0.2087
Epoch 2/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.1029 - loss: 4.0288 - top-5-accuracy: 0.2978 - val_accuracy: 0.0831 - val_loss: 5.0064 - val_top-5-accuracy: 0.2586
Epoch 3/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.1378 - loss: 3.8494 - top-5-accuracy: 0.3716 - val_accuracy: 0.0988 - val_loss: 4.8977 - val_top-5-accuracy: 0.2889
Epoch 4/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.1645 - loss: 3.7276 - top-5-accuracy: 0.4137 - val_accuracy: 0.1122 - val_loss: 4.6032 - val_top-5-accuracy: 0.3353
Epoch 5/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.1834 - loss: 3.6294 - top-5-accuracy: 0.4497 - val_accuracy: 0.1174 - val_loss: 4.6568 - val_top-5-accuracy: 0.3346
Epoch 6/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2004 - loss: 3.5588 - top-5-accuracy: 0.4747 - val_accuracy: 0.1228 - val_loss: 4.5376 - val_top-5-accuracy: 0.3487
Epoch 7/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2151 - loss: 3.4962 - top-5-accuracy: 0.4968 - val_accuracy: 0.1074 - val_loss: 4.9529 - val_top-5-accuracy: 0.3326
Epoch 8/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2335 - loss: 3.4458 - top-5-accuracy: 0.5116 - val_accuracy: 0.1223 - val_loss: 4.7854 - val_top-5-accuracy: 0.3429
Epoch 9/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.2427 - loss: 3.3955 - top-5-accuracy: 0.5275 - val_accuracy: 0.1159 - val_loss: 5.0100 - val_top-5-accuracy: 0.3406
Epoch 10/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2476 - loss: 3.3648 - top-5-accuracy: 0.5325 - val_accuracy: 0.1116 - val_loss: 5.2325 - val_top-5-accuracy: 0.3276
Epoch 11/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2567 - loss: 3.3301 - top-5-accuracy: 0.5476 - val_accuracy: 0.1261 - val_loss: 4.9936 - val_top-5-accuracy: 0.3409
Epoch 12/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2675 - loss: 3.2927 - top-5-accuracy: 0.5563 - val_accuracy: 0.1321 - val_loss: 4.8763 - val_top-5-accuracy: 0.3490
Epoch 13/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2680 - loss: 3.2709 - top-5-accuracy: 0.5650 - val_accuracy: 0.1245 - val_loss: 5.1547 - val_top-5-accuracy: 0.3404
Epoch 14/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.2845 - loss: 3.2266 - top-5-accuracy: 0.5795 - val_accuracy: 0.1375 - val_loss: 4.9445 - val_top-5-accuracy: 0.3581
Epoch 15/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.2865 - loss: 3.2079 - top-5-accuracy: 0.5874 - val_accuracy: 0.1418 - val_loss: 4.9763 - val_top-5-accuracy: 0.3582
Epoch 16/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.2897 - loss: 3.1846 - top-5-accuracy: 0.5911 - val_accuracy: 0.1307 - val_loss: 5.1843 - val_top-5-accuracy: 0.3488
Epoch 17/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3020 - loss: 3.1492 - top-5-accuracy: 0.6004 - val_accuracy: 0.1436 - val_loss: 4.9738 - val_top-5-accuracy: 0.3705
Epoch 18/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3064 - loss: 3.1178 - top-5-accuracy: 0.6112 - val_accuracy: 0.1315 - val_loss: 5.3203 - val_top-5-accuracy: 0.3506
Epoch 19/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3121 - loss: 3.1007 - top-5-accuracy: 0.6169 - val_accuracy: 0.1517 - val_loss: 4.8716 - val_top-5-accuracy: 0.3772
Epoch 20/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3165 - loss: 3.0770 - top-5-accuracy: 0.6239 - val_accuracy: 0.1292 - val_loss: 5.2754 - val_top-5-accuracy: 0.3565
Epoch 21/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3260 - loss: 3.0571 - top-5-accuracy: 0.6265 - val_accuracy: 0.1517 - val_loss: 4.9253 - val_top-5-accuracy: 0.3765
Epoch 22/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3315 - loss: 3.0374 - top-5-accuracy: 0.6355 - val_accuracy: 0.1420 - val_loss: 5.0759 - val_top-5-accuracy: 0.3693
Epoch 23/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3316 - loss: 3.0307 - top-5-accuracy: 0.6352 - val_accuracy: 0.1579 - val_loss: 4.8387 - val_top-5-accuracy: 0.3809
Epoch 24/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3338 - loss: 3.0089 - top-5-accuracy: 0.6445 - val_accuracy: 0.1517 - val_loss: 5.0654 - val_top-5-accuracy: 0.3673
Epoch 25/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3382 - loss: 3.0029 - top-5-accuracy: 0.6451 - val_accuracy: 0.1535 - val_loss: 5.0329 - val_top-5-accuracy: 0.3742
Epoch 26/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3448 - loss: 2.9714 - top-5-accuracy: 0.6493 - val_accuracy: 0.1590 - val_loss: 4.8344 - val_top-5-accuracy: 0.3839
Epoch 27/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3533 - loss: 2.9568 - top-5-accuracy: 0.6582 - val_accuracy: 0.1608 - val_loss: 4.9081 - val_top-5-accuracy: 0.3873
Epoch 28/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3537 - loss: 2.9458 - top-5-accuracy: 0.6625 - val_accuracy: 0.1568 - val_loss: 4.9791 - val_top-5-accuracy: 0.3727
Epoch 29/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3541 - loss: 2.9362 - top-5-accuracy: 0.6622 - val_accuracy: 0.1531 - val_loss: 4.9535 - val_top-5-accuracy: 0.3818
Epoch 30/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3620 - loss: 2.9063 - top-5-accuracy: 0.6708 - val_accuracy: 0.1528 - val_loss: 4.9747 - val_top-5-accuracy: 0.3713
Epoch 31/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3665 - loss: 2.9046 - top-5-accuracy: 0.6717 - val_accuracy: 0.1634 - val_loss: 4.9506 - val_top-5-accuracy: 0.3865
Epoch 32/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3680 - loss: 2.8889 - top-5-accuracy: 0.6751 - val_accuracy: 0.1574 - val_loss: 5.1366 - val_top-5-accuracy: 0.3665
Epoch 33/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3806 - loss: 2.8523 - top-5-accuracy: 0.6863 - val_accuracy: 0.1689 - val_loss: 4.8796 - val_top-5-accuracy: 0.3848
Epoch 34/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3812 - loss: 2.8454 - top-5-accuracy: 0.6877 - val_accuracy: 0.1512 - val_loss: 5.1448 - val_top-5-accuracy: 0.3725
Epoch 35/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3801 - loss: 2.8481 - top-5-accuracy: 0.6859 - val_accuracy: 0.1616 - val_loss: 5.0463 - val_top-5-accuracy: 0.3817
Epoch 36/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3846 - loss: 2.8313 - top-5-accuracy: 0.6879 - val_accuracy: 0.1652 - val_loss: 5.0744 - val_top-5-accuracy: 0.3863
Epoch 37/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3862 - loss: 2.8218 - top-5-accuracy: 0.6912 - val_accuracy: 0.1653 - val_loss: 4.9966 - val_top-5-accuracy: 0.3881
Epoch 38/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3915 - loss: 2.8045 - top-5-accuracy: 0.7003 - val_accuracy: 0.1684 - val_loss: 4.9768 - val_top-5-accuracy: 0.3945
Epoch 39/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 181ms/step - accuracy: 0.3888 - loss: 2.8025 - top-5-accuracy: 0.6986 - val_accuracy: 0.1750 - val_loss: 4.9214 - val_top-5-accuracy: 0.3931
Epoch 40/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.3956 - loss: 2.7918 - top-5-accuracy: 0.7039 - val_accuracy: 0.1645 - val_loss: 5.0248 - val_top-5-accuracy: 0.3962
Epoch 41/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 183ms/step - accuracy: 0.3984 - loss: 2.7769 - top-5-accuracy: 0.7041 - val_accuracy: 0.1644 - val_loss: 5.0712 - val_top-5-accuracy: 0.3891
Epoch 42/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 183ms/step - accuracy: 0.4065 - loss: 2.7514 - top-5-accuracy: 0.7145 - val_accuracy: 0.1644 - val_loss: 5.1896 - val_top-5-accuracy: 0.3805
Epoch 43/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 183ms/step - accuracy: 0.4024 - loss: 2.7514 - top-5-accuracy: 0.7103 - val_accuracy: 0.1695 - val_loss: 5.0084 - val_top-5-accuracy: 0.3912
Epoch 44/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 183ms/step - accuracy: 0.4098 - loss: 2.7455 - top-5-accuracy: 0.7173 - val_accuracy: 0.1795 - val_loss: 4.9562 - val_top-5-accuracy: 0.3955
Epoch 45/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 183ms/step - accuracy: 0.4116 - loss: 2.7289 - top-5-accuracy: 0.7190 - val_accuracy: 0.1734 - val_loss: 5.0107 - val_top-5-accuracy: 0.3965
Epoch 46/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.4153 - loss: 2.7149 - top-5-accuracy: 0.7233 - val_accuracy: 0.1712 - val_loss: 4.9779 - val_top-5-accuracy: 0.3913
Epoch 47/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.4169 - loss: 2.7148 - top-5-accuracy: 0.7234 - val_accuracy: 0.1698 - val_loss: 5.0097 - val_top-5-accuracy: 0.3908
Epoch 48/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.4222 - loss: 2.6960 - top-5-accuracy: 0.7260 - val_accuracy: 0.1676 - val_loss: 5.0487 - val_top-5-accuracy: 0.3952
Epoch 49/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.4247 - loss: 2.6861 - top-5-accuracy: 0.7299 - val_accuracy: 0.1690 - val_loss: 5.0369 - val_top-5-accuracy: 0.3897
Epoch 50/50
313/313 ━━━━━━━━━━━━━━━━━━━━ 57s 182ms/step - accuracy: 0.4279 - loss: 2.6776 - top-5-accuracy: 0.7329 - val_accuracy: 0.1694 - val_loss: 5.1839 - val_top-5-accuracy: 0.3785

演绎展示：

理想状态：

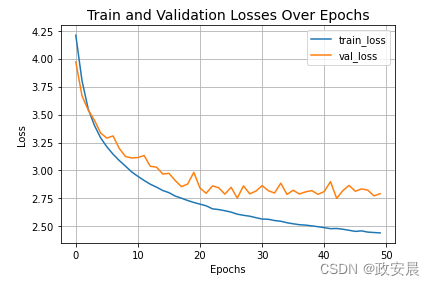
让我们来看看 CIFAR-100 的最终测试结果。

演绎展示：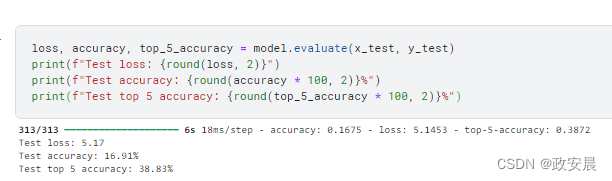
EANet 只

是用外部注意力取代了 Vit 中的自我注意力。传统的 Vit 在训练了 50 个 epoch 之后，测试前 5 名的准确率达到了约 73%，前 1 名的准确率达到了约 41%，但参数为 0.6M。

在相同的实验环境和超参数下，我们刚刚训练的 EANet 模型只有 0.3M 个参数，就能达到 ~73% 的测试 top-5 准确率和 ~43% 的 top-1 准确率。这充分证明了外部注意力的有效性。

我们只展示了 EANet 的训练过程，您可以在相同的实验条件下训练 Vit 并观察测试结果。