Abstract 摘要
Recent studies in Radiance Fields have paved the robust way for novel view synthesis with their photorealistic rendering quality. Nevertheless, they usually employ neural networks and volumetric rendering, which are costly to train and impede their broad use in various real-time applications due to the lengthy rendering time. Lately 3D Gaussians splatting-based approach has been proposed to model the 3D scene, and it achieves remarkable visual quality while rendering the images in real-time. However, it suffers from severe degradation in the rendering quality if the training images are blurry. Blurriness commonly occurs due to the lens defocusing, object motion, and camera shake, and it inevitably intervenes in clean image acquisition. Several previous studies have attempted to render clean and sharp images from blurry input images using neural fields. The majority of those works, however, are designed only for volumetric rendering-based neural radiance fields and are not straightforwardly applicable to rasterization-based 3D Gaussian splatting methods. Thus, we propose a novel real-time deblurring framework, deblurring 3D Gaussian Splatting, using a small Multi-Layer Perceptron (MLP) that manipulates the covariance of each 3D Gaussian to model the scene blurriness. While deblurring 3D Gaussian Splatting can still enjoy real-time rendering, it can reconstruct fine and sharp details from blurry images. A variety of experiments have been conducted on the benchmark, and the results have revealed the effectiveness of our approach for deblurring. Qualitative results are available at Deblurring 3D Gaussian Splatting
最近的研究在辐射领域铺平了道路,为新的视图合成与他们的真实感渲染质量。然而,它们通常采用神经网络和体积渲染,这是昂贵的训练和阻碍其广泛使用的各种实时应用程序由于漫长的渲染时间。近年来提出了一种基于三维高斯分裂的三维场景建模方法,并在实时绘制图像的同时获得了良好的视觉效果。然而,如果训练图像是模糊的,它遭受严重的渲染质量下降。模糊通常是由于透镜散焦、物体运动和相机抖动而发生的,并且它不可避免地干扰了清晰图像的获取。之前的几项研究试图使用神经场从模糊的输入图像中渲染干净清晰的图像。 然而,这些作品中的大多数仅针对基于体积渲染的神经辐射场而设计,并且不直接适用于基于光栅化的3D高斯溅射方法。因此,我们提出了一种新的实时去模糊框架,去模糊3D高斯飞溅,使用一个小的多层感知器(MLP),操纵每个3D高斯的协方差模型的场景模糊。虽然去模糊3D高斯溅射仍然可以享受实时渲染,但它可以从模糊图像中重建精细和清晰的细节。在基准上进行了各种实验,结果表明了该方法的有效性。定性结果见https://benhenryl.github。io/去模糊-3D-Gaussian-Splatting/ Deblurring 3D Gaussian Splatting
1Introduction 1介绍
With the emergence of Neural Radiance Fields (NeRF) [23], Novel view synthesis (NVS) has accounted for more roles in computer vision and graphics with its photorealistic scene reconstruction and applicability to diverse domains such as augmented/virtual reality(AR/VR) and robotics. Various NVS methods typically involve modeling 3D scenes from multiple 2D images from arbitrary viewpoints, and these images are often taken under diverse conditions. One of the significant challenges, particularly in practical scenarios, is the common occurrence of blurring effects. It has been a major bottleneck in rendering clean and high-fidelity novel view images, as it requires accurately reconstructing the 3D scene from the blurred input images.
随着神经辐射场(NeRF)[ 23]的出现,新视图合成(NVS)在计算机视觉和图形学中占据了更多的角色,其逼真的场景重建和适用于增强/虚拟现实(AR/VR)和机器人等不同领域。各种NVS方法通常涉及从任意视点从多个2D图像建模3D场景,并且这些图像通常在不同条件下拍摄。其中一个重大挑战,特别是在实际场景中,是模糊效果的常见发生。它一直是绘制干净和高保真的新视图图像的主要瓶颈,因为它需要从模糊的输入图像精确地重建3D场景。
NeRF [23] has shown outstanding performance in synthesizing photo-realistic images for novel viewpoints by representing 3D scenes with implicit functions. The volume rendering [7] technique has been a critical component of the massive success of NeRF. This can be attributed to its continuous nature and differentiability, making it well-suited to today’s prevalent automatic differentiation software ecosystems. However, significant rendering and training costs are associated with the volumetric rendering approach due to its reliance on dense sampling along the ray to generate a pixel, which requires substantial computational resources. Despite the recent advancements [10, 38, 24, 8, 9] that significantly reduce training time from days to minutes, improving the rendering time still remains a vital challenge.
NeRF [ 23]通过用隐式函数表示3D场景,在合成新颖视点的照片级逼真图像方面表现出出色的性能。体绘制[ 7]技术是NeRF取得巨大成功的关键组成部分。这可以归因于其连续性和差异性,使其非常适合当今流行的自动差异化软件生态系统。然而,显著的渲染和训练成本与体积渲染方法相关联,这是由于其依赖于沿射线沿着密集采样以生成像素,这需要大量的计算资源。尽管最近的进步[ 10,38,24,8,9]显着减少训练时间从几天到几分钟,提高渲染时间仍然是一个至关重要的挑战。
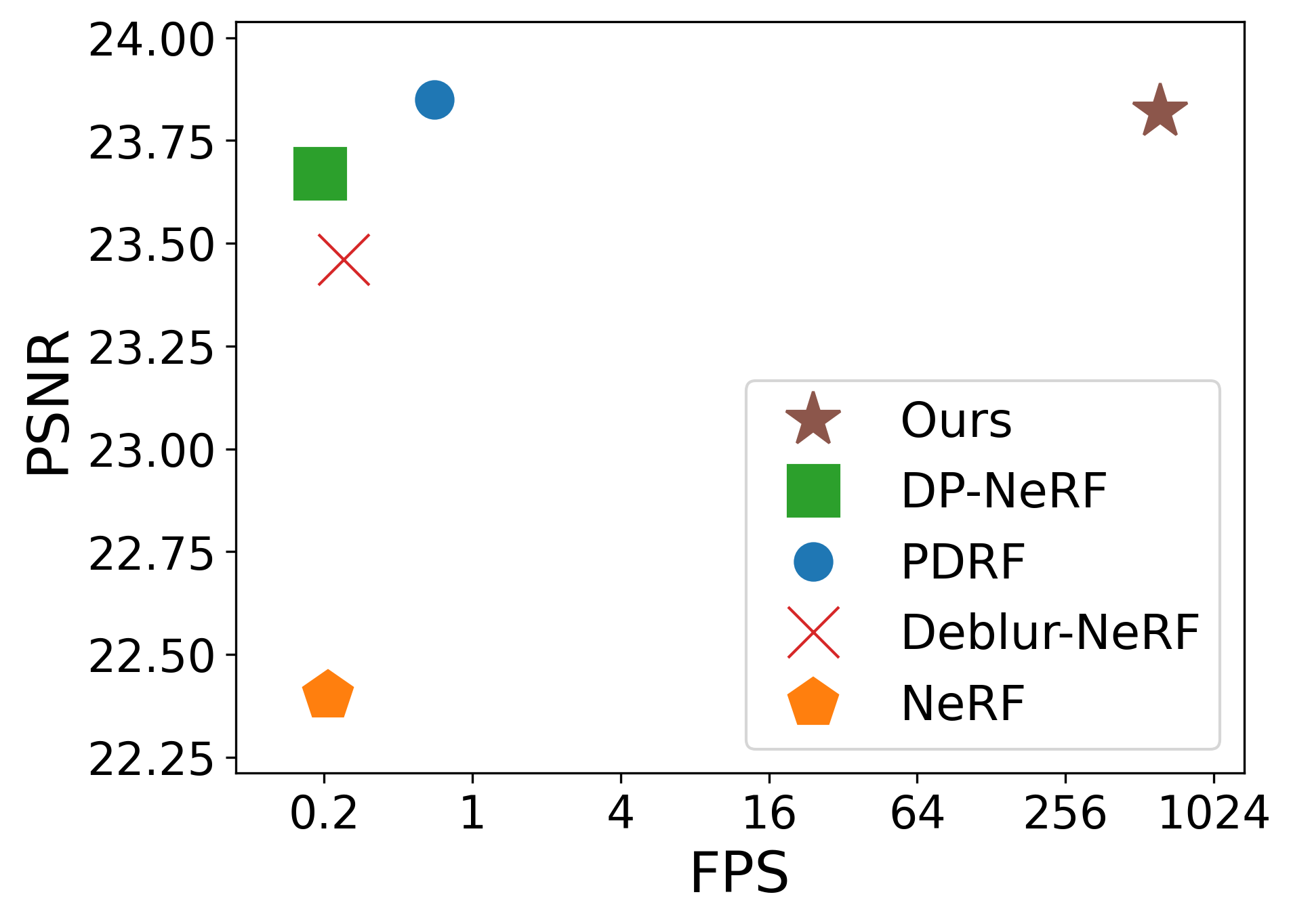
Figure 1:Performance comparison to state-of-the-art deblurring NeRFs. Ours achieved a fast rendering speed (200 fps vs. 1 fps) while maintaining competitive rendered image quality (x-axis is represented in log scale).
图1:与最先进的去模糊NeRF的性能比较。我们的实现了快速渲染速度(200 fps vs. 1 fps),同时保持了具有竞争力的渲染图像质量(x轴以对数标度表示)。
Recently, 3D Gaussian Splatting (3D-GS) [15] has gained significant attention, demonstrating a capability to produce high-quality images at a remarkably fast rendering speed. It combines a large number of colored 3D Gaussians to represent 3D scenes with a differentiable splatting-based rasterization, substituting NeRF’s time-demanding volumetric rendering. The rendering process projects 3D Gaussian points onto the 2D image planes, and the positions, sizes, rotations, colors, and opacities of these Gaussians are adjusted via gradient-based optimization to better capture the 3D scenes. 3D-GS leverages rasterization, which can be significantly more efficient than volume rendering techniques on modern graphics hardware, thereby enabling rapid real-time rendering.
最近,3D高斯溅射(3D-GS)[ 15]获得了极大的关注,证明了以非常快的渲染速度生成高质量图像的能力。它结合了大量的彩色3D高斯来表示3D场景,并使用可区分的基于splatting的光栅化,取代了NeRF的时间要求很高的体积渲染。渲染过程将3D高斯点投影到2D图像平面上,并且通过基于梯度的优化来调整这些高斯点的位置、大小、旋转、颜色和不透明度,以更好地捕获3D场景。3D-GS利用光栅化,这可以比现代图形硬件上的体渲染技术更有效,从而实现快速实时渲染。
Expanding on the impressive capabilities of 3D-GS, we aim to further improve its robustness and versatility for more realistic settings, especially those involving blurring effects. Several approaches have attempted to handle the blurring issues in the recent NeRF literature [22, 20, 6, 41, 43]. The pioneering work is Deblur-NeRF [22], which renders sharp images from the neural radiance fields and uses an extra multi-layer perceptron (MLP) to produce the blur kernels. DP-NeRF [20] constrains neural radiance fields with two physical priors derived from the actual blurring process to reconstruct clean images. PDRF [28] uses a two-stage deblurring scheme and a voxel representation to further improve deblurring and training time. All works mentioned above have been developed under the assumption of volumetric rendering, which is not straightforwardly applicable to rasterization-based 3D-GS. Another line of works [41, 6], though not dependent on volume rendering, only address a specific type of blur, i.e., camera motion blur, and are not valid for mitigating the defocus blur.
扩展3D-GS令人印象深刻的功能,我们的目标是进一步提高其鲁棒性和多功能性,以实现更逼真的设置,特别是那些涉及模糊效果的设置。在最近的NeRF文献中,有几种方法试图处理模糊问题[ 22,20,6,41,43]。开创性的工作是Deflur-NeRF [ 22],它从神经辐射场呈现清晰的图像,并使用额外的多层感知器(MLP)来产生模糊内核。DP-NeRF [ 20]使用从实际模糊过程中导出的两个物理先验来约束神经辐射场,以重建干净的图像。PDRF [ 28]使用两阶段去模糊方案和体素表示来进一步改善去模糊和训练时间。上述所有工作都是在体绘制的假设下开发的,这并不直接适用于基于光栅化的3D-GS。 另一行作品[ 41,6]虽然不依赖于体绘制,但仅解决了特定类型的模糊,即,相机运动模糊,并且对于减轻散焦模糊无效。
In this work, we propose Deblurring 3D-GS, the first defocus deblurring algorithm for 3D-GS, which is well aligned with rasterization and thus enables real-time rendering. To do so, we modify the covariance matrices of 3D Gaussians to model the blurriness. Specifically, we employ a small MLP, which manipulates the covariance of each 3D Gaussian to model the scene blurriness. As blurriness is a phenomenon that is based on the intermingling of the neighboring pixels, our Deblurring 3D-GS simulates such an intermixing during the training time. To this end, we designed a framework that utilizes an MLP to learn the variations in different attributes of 3D Gaussians. These small variations are multiplied to the original values of the attributes, which in turn determine the updated shape of the resulting Gaussians. During the inference time, we render the scene using only the original components of 3D-GS without any additional offsets from MLP; thereby, 3D-GS can render sharp images because each pixel is free from the intermingling of nearby pixels. Further, since the MLP is not activated during the inference time, it can still enjoy real-time rendering similar to the 3D-GS while it can reconstruct fine and sharp details from the blurry images.
在这项工作中,我们提出了去模糊3D-GS,第一个散焦去模糊算法的3D-GS,这是很好地对准光栅化,从而使实时渲染。为此,我们修改3D高斯的协方差矩阵来对模糊度进行建模。具体来说,我们采用了一个小的MLP,它操纵每个3D高斯的协方差模型的场景模糊。由于模糊是一种基于相邻像素混合的现象,因此我们的Deflurring 3D-GS在训练时间内模拟了这种混合。为此,我们设计了一个框架,利用MLP来学习3D高斯的不同属性的变化。这些小的变化被乘以属性的原始值,这反过来又决定了结果高斯的更新形状。 在推理期间,我们仅使用3D-GS的原始组件渲染场景,而不使用来自MLP的任何额外偏移;因此,3D-GS可以渲染清晰的图像,因为每个像素都没有与附近像素的混合。此外,由于MLP在推理时间期间不被激活,因此它仍然可以享受类似于3D-GS的实时渲染,同时它可以从模糊图像重建精细和清晰的细节。

Figure 2:Our method’s overall workflow. �(⋅) denotes positional encoding, ⊙ denotes hadamard product, and �, �, � stand for position, quaternion, and scaling of 3D Gaussian respectively. Given a set of 3D Gaussians �, we extract �, �, � from each 3D Gaussian. Viewing direction � from the dataset and � are positionally encoded and then fed to ��, a small MLP parameterized with �, which yields offsets �� and �� for each Gaussian. These �� and �� are element-wisely multiplied to their respective Gaussians’s � and � respectively, and these computed attributes are used to construct transformed 3D Gaussians �′(�,�⋅��,�⋅��). These transformed Gaussians �′ are differentiably rasterized to render blurred image during training time. However, for inference stage, � is directly fed to differentiable rasterizer, without involving any MLP, to render sharp image.
图2:我们的方法的总体工作流程。 �(⋅) 表示位置编码, ⊙ 表示hadamard积, � 、 � 、 � 分别代表3D高斯的位置、四元数和缩放。给定一组3D高斯 � ,我们从每个3D高斯中提取 � , � , � 。对来自数据集的观看方向 � 和 � 进行位置编码,然后将其馈送到 �� ,即用 � 参数化的小MLP,这为每个高斯产生偏移 �� 和 �� 。将这些 �� 和 �� 分别逐元素地乘以它们各自的高斯 � 和 � ,并且这些计算的属性用于构造变换的3D高斯 �′(�,�⋅��,�⋅��) 。这些变换后的高斯 �′ 在训练时间期间被可微分地光栅化以渲染模糊图像。然而,对于推理阶段, � 被直接馈送到可微分光栅化器,而不涉及任何MLP,以呈现清晰的图像。
3D-GS [15] models a 3D scene from a sparse point cloud, which is usually obtained from the structure-from-motion (SfM) [35]. SfM extracts features from multi-view images and relates them via 3D points in the scene. If the given images are blurry, SfM fails heavily in identifying the valid features, and ends up extracting a very small number of points. Even worse, if the scene has a larger depth of field, SfM hardly extracts any points which lie on the far end of the scene. Due to this excessive sparsity in the point cloud constructed from set of blurry images, existing methods, including 3D-GS [15], that rely on point clouds fail to reconstruct the scene with fine details. To compensate for this excessive sparsity, we propose to add extra points with valid color features to the point cloud using N-nearest-neighbor interpolation [29]. In addition, we prune Gaussians based on their position to keep more Gaussians on the far plane.
3D-GS [ 15]从稀疏点云建模3D场景,稀疏点云通常从运动恢复结构(SfM)[ 35]获得。SfM从多视图图像中提取特征,并通过场景中的3D点将它们关联起来。如果给定的图像是模糊的,SfM在识别有效特征时会严重失败,最终提取的点数量非常少。更糟糕的是,如果场景具有较大的景深,则SfM几乎无法提取位于场景远端的任何点。由于从一组模糊图像构建的点云中的这种过度稀疏性,依赖于点云的现有方法(包括3D-GS [ 15])无法重建具有精细细节的场景。为了补偿这种过度的稀疏性,我们建议使用N-最近邻插值向点云添加具有有效颜色特征的额外点[ 29]。此外,我们根据高斯分布的位置对它们进行修剪,以使更多的高斯分布保持在远平面上。
A variety of experiments have been conducted on the benchmark, and the results have revealed the effectiveness of our approach for deblurring. Tested under different evaluation matrices, our method achieves state-of-the-art rendering quality or performs on par with the currently leading models while achieving significantly faster rendering speed (> 200 FPS)
在基准上进行了各种实验,结果表明了该方法的有效性。在不同的评估矩阵下进行测试,我们的方法达到了最先进的渲染质量或与当前领先的模型相当,同时实现了更快的渲染速度( > 200 FPS)
To sum up, our contributions are the following:
总而言之,我们的贡献如下:
- •
We propose the first real-time rendering-enabled defocus deblurring framework using 3D-GS.
·我们提出了第一个使用3D-GS的实时渲染支持的散焦去模糊框架。 - •
We propose a novel technique that manipulates the covariance matrix of each 3D Gaussian differently to model spatially changing blur using a small MLP.
·我们提出了一种新的技术,该技术不同地操纵每个3D高斯的协方差矩阵,以使用小的MLP来对空间变化的模糊进行建模。 - •
To compensate for sparse point clouds due to the blurry images, we propose a training technique that prunes and adds extra points with valid color features so that we can put more points on the far plane of the scene and harshly blurry regions.
·为了补偿由于模糊图像而导致的稀疏点云,我们提出了一种训练技术,该技术可以修剪并添加具有有效颜色特征的额外点,以便我们可以将更多点放在场景的远平面和严重模糊的区域上。 - •
We achieve FPS > 200 while accomplishing superior rendering quality or performing on par with the existing cutting-edge models under different metrics.
·我们实现了FPS > 200,同时实现了上级渲染质量或在不同指标下与现有尖端模型的性能相当。
2Related Works 2相关作品
2.1Image Deblurring 2.1图像去模糊
It is common to observe that when we casually take pictures with optical imaging systems, some parts of scene appear blurred in the images. This blurriness is caused by a variety of factors, including object motion, camera shake, and lens defocusing [1, 34]. When the image plane is separated from the ideal reference plane during the imaging process, out-of-focus or defocus blur happens. The degradation induced by defocus blur of an image is generally expressed as follows:
当我们用光学成像系统随意拍照时,我们经常会观察到场景的某些部分在图像中出现模糊。这种模糊是由多种因素引起的,包括物体运动、相机抖动和透镜散焦[ 1,34]。在成像过程中,当像面与理想参考面分离时,会产生离焦或散焦模糊。由图像的散焦模糊引起的劣化通常表示如下:
| �(�)=∑�∈�ℎℎ(�,�)�(�)+�(�),�∈��, | (1) |
where �(�) represents an observed blurry image, ℎ(�,�) is a blur kernel or Point Spread Function (PSF), �(�) is a latent sharp image, and �(�) denotes an additive white Gaussian noise that frequently occurs in nature images. ��⊂ℝ2 is a support set of an image and �ℎ⊂ℝ2 is a support set of a blur kernel or PSF [18].
其中 �(�) 表示观察到的模糊图像, ℎ(�,�) 是模糊核或点扩散函数(PSF), �(�) 是潜在清晰图像,而 �(�) 表示在自然图像中频繁出现的加性白色高斯噪声。 ��⊂ℝ2 是图像的支持集, �ℎ⊂ℝ2 是模糊内核或PSF的支持集[ 18]。
The first canonical approach to deconvolve an image is [33]. It applies iterative minimization to an energy function to obtain a maximum likelihood approximation of the original image, using a known PSF (the blur kernel). Typically, the blurring kernel � and the sharp image � are unknown. The technique termed as image blind deblurring [42] involves recovering the latent sharp image given just one blurry image �. In this procedure, the deblurred image is obtained by first estimating a blurring kernel. Image blind deblurring is a long-standing and ill-posed problem in the field of image and vision. Numerous approaches to address the blurring issue have been suggested in the literature. Among them, traditional methods often construct deblurring as an optimization problem and rely on natural image priors [21, 26, 44, 47]. Conversely, the majority of deep learning-based techniques use convolutional neural networks (CNN) to map the blurry image with the latent sharp image directly [25, 46, 31]. While series of studies have been actively conducted for image deblurring, they are mainly designed for deblurring 2D images and are not easily applicable to 3D scenes deblurring due to the lack of 3D view consistency.
去卷积图像的第一个规范方法是[ 33]。它使用已知的PSF(模糊核)对能量函数进行迭代最小化,以获得原始图像的最大似然近似。通常,模糊核 � 和清晰图像 � 是未知的。被称为图像盲去模糊的技术[ 42]涉及在仅给定一个模糊图像 � 的情况下恢复潜在的清晰图像。在该过程中,通过首先估计模糊核来获得去模糊图像。图像盲去模糊是图像与视觉领域中一个长期存在的病态问题。在文献中已经提出了许多解决模糊问题的方法。其中,传统方法通常将去模糊构造为优化问题,并依赖于自然图像先验[ 21,26,44,47]。 相反,大多数基于深度学习的技术使用卷积神经网络(CNN)直接将模糊图像与潜在清晰图像映射[25,46,31]。虽然已经针对图像去模糊积极地进行了一系列研究,但是它们主要是针对2D图像去模糊而设计的,并且由于缺乏3D视图一致性而不容易适用于3D场景去模糊。
2.2Neural Radiance Fields
2.2神经辐射场
Neural Radiance Fields (NeRF) are a potent method that has recently gained popularity for creating high-fidelity 3D scenes from 2D images. Realistic rendering from novel viewpoints is made possible by NeRF, which uses deep neural networks to encode volumetric scene features. To estimate density �∈[0,∞) and color value �∈[0,1]3 of a given point, a radiance field is a continuous function � that maps a 3D location �∈ℝ3 and a viewing direction �∈𝕊2. This function has been parameterized by a multi-layer perceptron (MLP) [23], where the weights of MLP are optimized to reconstruct a series of input photos of a particular scene: (�,�)=��:(�(�),�(�)) Here, � indicates the network weights, and � is the specified positional encoding applied to � and � [39]. To generate the images at novel views, volume rendering [7] is used, taking into account the volume density and color of points.
神经辐射场(NeRF)是一种有效的方法,最近在从2D图像创建高保真3D场景方面越来越受欢迎。NeRF使新颖视角的真实感渲染成为可能,NeRF使用深度神经网络对体积场景特征进行编码。为了估计给定点的密度 �∈[0,∞) 和颜色值 �∈[0,1]3 ,辐射场是映射3D位置 �∈ℝ3 和观看方向 �∈𝕊2 的连续函数 � 。此函数已由多层感知器(MLP)参数化[ 23],其中MLP的权重经过优化以重建特定场景的一系列输入照片: (�,�)=��:(�(�),�(�)) 在此, � 表示网络权重, � 是应用于 � 和 � 的指定位置编码[ 39]。为了在新视图下生成图像,使用体积渲染[ 7],考虑点的体积密度和颜色。
2.2.1Fast Inference NeRF 2.2.1快速推理NeRF
Numerous follow-up studies have been carried out to enhance NeRF’s rendering time to achieve real-time rendering. Many methods, such as grid-based approaches [40, 4, 38, 3, 8, 32], or those relying on hash [24, 2] adopt additional data structures to effectively reduce the size and number of layers of MLP and successfully improve the inference speed. However, they still fail to reach real-time view synthesis. Another line of works [30, 13, 45] proposes to bake the trained parameters into the faster representation and attain real-time rendering. While these methods rely on volumetric rendering, recently, 3D-GS [15] successfully renders photo-realistic images at novel views with noticeable rendering speed using a differentiable rasterizer and 3D Gaussians. Although several approaches have attempted to render tens or hundreds of images in a second, deblurring the blurry scene in real-time is not addressed, while blurriness commonly hinders clean image acquisition in the wild.
许多后续研究已经进行,以提高NeRF的渲染时间,以实现实时渲染。许多方法,如基于网格的方法[ 40,4,38,3,8,32]或依赖于散列的方法[ 24,2],采用额外的数据结构来有效地减少MLP的大小和层数,并成功地提高推理速度。然而,他们仍然无法达到实时视图合成。另一行工作[ 30,13,45]建议将训练的参数烘焙到更快的表示中并实现实时渲染。虽然这些方法依赖于体积渲染,但最近,3D-GS [ 15]成功地使用可微分光栅化器和3D高斯以新颖的视图以显著的渲染速度渲染照片级逼真的图像。虽然有几种方法试图在一秒钟内渲染数十或数百张图像,但实时消除模糊场景的模糊并没有解决,而模糊通常会阻碍野外的清晰图像采集。
2.2.2Deblurring NeRF 2.2.2去模糊NeRF
Several strategies have been proposed to train NeRF to render clean and sharp images from blurry input images. While DoF-NeRF [43] attempts to deblur the blurry scene, both all-in-focus and blurry images are required to train the model. Deblur-NeRF [22] firstly suggests deblurring NeRF without any all-in-focus images during training. It employs an additional small MLP, which predicts per-pixel blur kernel. However, it has to render the neighboring pixels of the target pixel in advance to model the interference of the neighboring information, so it takes additional computation at the time of training. Though the inference stage does not involve the blur kernel estimation, it is no different from the training with regard to rendering time as it is based on volumetric rendering which takes several seconds to render a single image. DP-NeRF [19] improved Deblur-NeRF in terms of image quality, and PDRF [28] partially replaces MLP to the grid and ameliorates rendering speed, still they depend on volumetric rendering to produce images and are not free from the rendering cost. Other works [6, 41] are aimed at addressing another type of blur, camera motion blur, rather than solving the long rendering time. While these deblurring NeRFs successfully produce clean images from the blurry input images, there is room for improvement in terms of rendering time. Thus, we propose a novel deblurring framework, deblurring 3D Gaussian Splatting, which enables real-time sharp image rendering using a differentiable rasterizer and 3D Gaussians.
已经提出了几种策略来训练NeRF从模糊的输入图像渲染干净和清晰的图像。虽然DoF-NeRF [ 43]尝试去模糊场景,但训练模型需要全焦点和模糊图像。Deflur-NeRF [ 22]首先建议在训练期间在没有任何全聚焦图像的情况下对NeRF进行去模糊。它采用了一个额外的小MLP,预测每像素模糊内核。然而,它必须提前渲染目标像素的相邻像素来模拟相邻信息的干扰,因此在训练时需要额外的计算。虽然推理阶段不涉及模糊核估计,但它与渲染时间方面的训练没有什么不同,因为它是基于体积渲染的,渲染单个图像需要几秒钟。 DP-NeRF [ 19]在图像质量方面改进了Deflur-NeRF,PDRF [ 28]部分取代了网格的MLP并改善了渲染速度,但它们仍然依赖于体积渲染来生成图像,并且没有摆脱渲染成本。其他作品[ 6,41]旨在解决另一种类型的模糊,相机运动模糊,而不是解决长渲染时间。虽然这些去模糊NeRF成功地从模糊的输入图像中产生清晰的图像,但在渲染时间方面还有改进的空间。因此,我们提出了一种新的去模糊框架,去模糊3D高斯飞溅,它使实时清晰的图像渲染使用可微光栅化器和3D高斯。
3Deblurring 3D Gaussian Splatting
3Deflurring 3D Gaussian Splatting
Based on the 3D-GS [15], we generate 3D Gaussians, and each Gaussian is uniquely characterized by a set of the parameters, including 3D position �, opacity �, and covariance matrix derived from quaternion � scaling �. Each 3D Gaussian also contains spherical harmonics (SH) to represent view-dependent appearance. The input for the proposed method consists of camera poses and point clouds, which can be obtained through the structure from motion (SfM) [35], and a collection of images (possibly blurred). To deblur 3D Gaussians, we employ an MLP that takes the positions of the 3D Gaussians along with the � and � as inputs and outputs ��, and �� which are the small scaling factors multiplied to � and �, respectively. With new quaternion and scale, �⋅�� and �⋅��, the updated 3D Gaussians are subsequently fed to the tile-based rasterizer to produce the blurry images. The overview of our method is shown in Fig. 2.
基于3D-GS [ 15],我们生成3D高斯,每个高斯由一组参数唯一表征,包括3D位置 � ,不透明度 � 和从四元数 � 缩放 � 导出的协方差矩阵。每个3D高斯还包含球谐函数(SH)以表示视图相关外观。所提出的方法的输入包括相机姿态和点云,可以通过运动恢复结构(SfM)[ 35]和图像集合(可能模糊)获得。为了去模糊3D高斯,我们采用MLP,其将3D高斯的位置连同 � 和 � 一起沿着作为输入,并且输出 �� 和 �� ,其分别是乘以 � 和 � 的小缩放因子。使用新的四元数和比例 �⋅�� 和 �⋅�� ,更新的3D高斯随后被馈送到基于瓦片的光栅化器以产生模糊图像。我们的方法概述如图2所示。
3.1Differential Rendering via 3D Gaussian Splatting
3.1基于3D高斯散射的差分绘制
At the training time, the blurry images are rendered in a differentiable way and we use a gradient-based optimization to train our deblurring 3D Gaussians. We adopt methods from [15], which proposes differentiable rasterization. Each 3D Gaussian is defined by its covariance matrix Σ(�,�) with mean value in 3D world space � as following:
在训练时,模糊图像以可区分的方式渲染,我们使用基于梯度的优化来训练我们的去模糊3D高斯。我们采用[ 15]中的方法,该方法提出了可微光栅化。每个3D高斯由其协方差矩阵 Σ(�,�) 定义,其中3D世界空间 � 中的平均值如下:
| �(�,�,�)=�−12��Σ−1(�,�)�. | (2) |
Besides Σ(�,�) and �, 3D Gaussians are also defined with spherical harmonics coefficients (SH) to represent view-dependent appearance and opacity for alpha value. The covariance matrix is valid only when it satisfies positive semi-definite, which is challenging to constrain during the optimization. Thus, the covariance matrix is decomposed into two learnable components, a quaternion � for representing rotation and � for representing scaling, to circumvent the positive semi-definite constraint similar to the configuration of an ellipsoid. � and � are transformed into rotation matrix and scaling matrix, respectively, and construct Σ(�,�) as follows:
除了 Σ(�,�) 和 � 之外,还使用球谐系数(SH)来定义3D高斯,以表示alpha值的视图相关外观和不透明度。协方差矩阵只有在满足半正定时才有效,这在优化过程中具有挑战性。因此,协方差矩阵被分解成两个可学习的分量,用于表示旋转的四元数 � 和用于表示缩放的四元数 � ,以规避类似于椭圆体的配置的半正定约束。将 � 和 � 分别变换为旋转矩阵和缩放矩阵,并如下构造 Σ(�,�) :
| Σ(�,�)=�(�)�(�)�(�)��(�)�, | (3) |
where �(�) is a rotation matrix given the rotation parameter � and �(�) is a scaling matrix from the scaling parameter � [17]. These 3D Gaussians are projected to 2D space [48] to render 2D images with following 2D covariance matrix Σ′(�,�):
其中 �(�) 是给定旋转参数 � 的旋转矩阵,并且 �(�) 是来自缩放参数 � 的缩放矩阵[ 17]。将这些3D高斯投影到2D空间[ 48]以使用以下2D协方差矩阵 Σ′(�,�) 渲染2D图像:
| Σ′(�,�)=��Σ(�,�)����, | (4) |
where � denotes the Jacobian of the affine approximation of the projective transformation, � stands for the world-to-camera matrix. Each pixel value is computed by accumulating � ordered projected 2D Gaussians overlaid on the each pixel with the formula:
其中 � 表示投影变换的仿射近似的雅可比矩阵, � 表示世界到相机矩阵。每个像素值是通过用以下公式累积覆盖在每个像素上的 � 有序投影2D高斯来计算的:
| �=∑�∈������� with ��=∏�=1�−1(1−��), | (5) |
�� is the color of each point, and �� is the transmittance. ��∈[0,1] defined by 1−exp−���� where �� and �� are the density of the point and the interval along the ray respectively. For further details, please refer to the original paper [15].
�� 是每个点的颜色, �� 是透射率。其中 �� 和 �� 分别是点的密度和沿射线的沿着间隔。有关详细信息,请参阅原始文件[ 15]。
3.2Deblurring 3D Gaussians
3.2去模糊3D高斯
3.2.1Motivation
It is discussed in eq. 1 that the pixels in images get blurred due to defocusing, and this phenomenon is usually modeled through a convolution operation. According to the thin lens law [12], the scene points that lie at the focal distance of the camera make a sharp image at the imaging plane. On the other hand, any scene points that are not at the focal distance will make a blob instead of a sharp point on the imaging plane, and it produces a blurred image. If the separation from the focal distance of a scene point is large, it produces a blob of a large area, which corresponds to severe blur. This blurring effect is usually modeled by a 2D Gaussian function known as the point spread function (PSF). Correspondingly, an image captured by a camera is the result of the convolution of the actual image and the PSF. Through this convolution, which is the weighted summation of neighboring pixels, few pixels can affect the central pixel heavily depending on the weight. In other words, in the defocus imaging process, a pixel affects the intensity of neighboring pixels. This theoretical base provides us the motivation to build our deblurring 3D Gaussians framework. We assume that big sized 3D Gaussians cause the blur, while relatively smaller 3D Gaussians correspond to the sharp image. This is because those with greater dispersion are affected by more neighboring information as they are responsible for wider regions in image space, so they can represent the interference of the neighboring pixels. Whereas the fine details in the 3D scene can be better modeled through the smaller 3D Gaussians.
在EQ中讨论。1中,图像中的像素由于散焦而变得模糊,并且这种现象通常通过卷积运算来建模。根据薄透镜定律[ 12],位于相机焦距处的场景点在成像平面处形成清晰的图像。另一方面,任何不在焦距处的场景点将在成像平面上形成斑点而不是尖锐点,并且它产生模糊图像。如果与场景点的焦距的分离较大,则其产生大面积的斑点,这对应于严重的模糊。这种模糊效果通常由称为点扩散函数(PSF)的2D高斯函数建模。相应地,由相机捕获的图像是实际图像和PSF的卷积的结果。通过这种卷积,即相邻像素的加权求和,很少有像素会严重影响中心像素,这取决于权重。 换句话说,在散焦成像处理中,像素影响相邻像素的强度。这个理论基础为我们提供了构建去模糊3D高斯框架的动力。我们假设大尺寸的3D高斯引起模糊,而相对较小的3D高斯对应于清晰的图像。这是因为那些具有较大分散性的像素受到更多相邻信息的影响,因为它们负责图像空间中更宽的区域,因此它们可以表示相邻像素的干扰。而3D场景中的精细细节可以通过较小的3D高斯模型更好地建模。
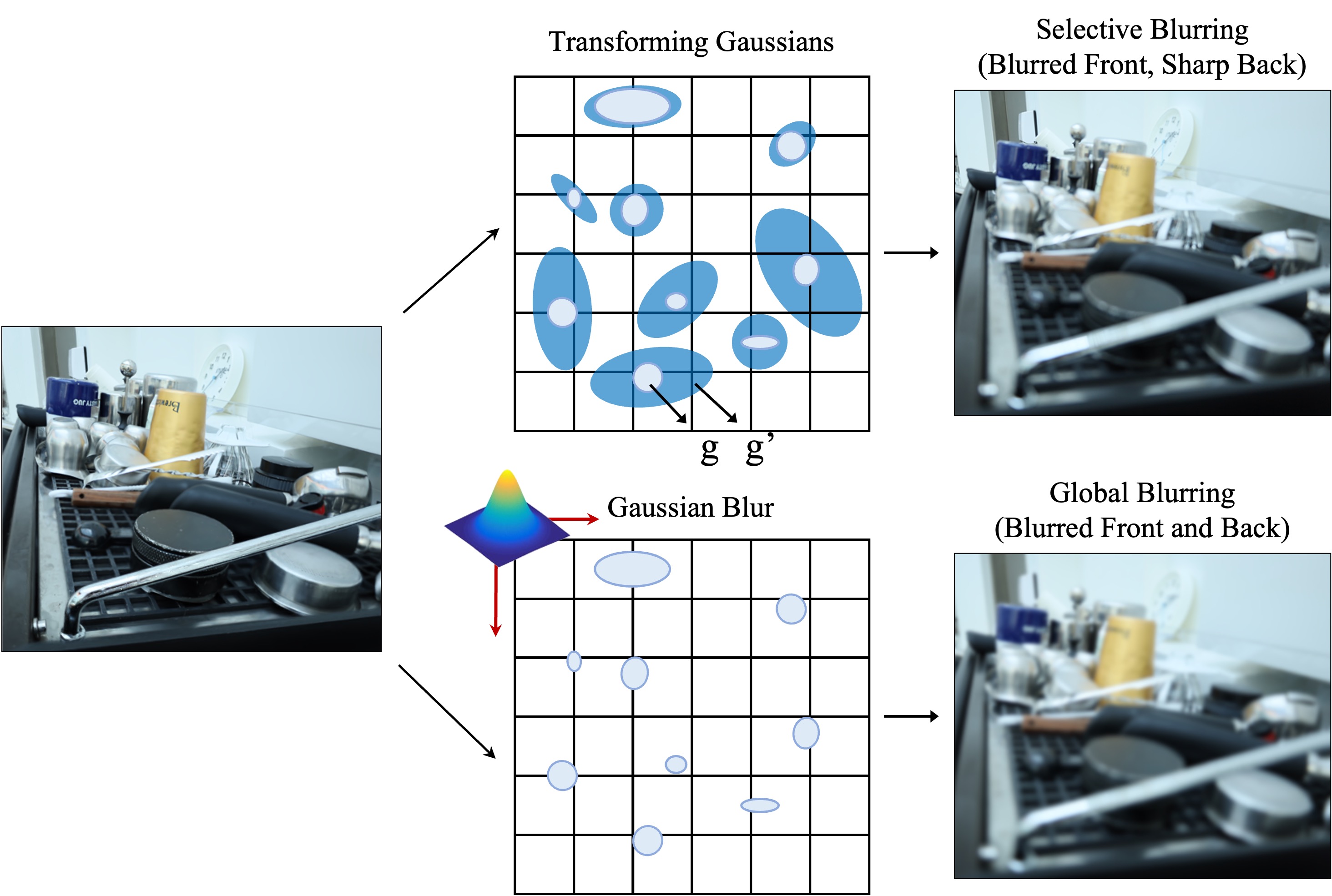
Figure 3:Comparison to normal Gaussian blur kernel. Top row: It shows the proposed method. � is the Gaussian before the transformation, and �′ is the Gaussian after the transformation. Since the different transformations can be applied to different Gaussian, ours can selectively blur the images depending on the scene; it can only blur the front parts of the scene. Bottom row: It shows a normal Gaussian blur kernel, which is not capable of handling different parts of the image differently, thereby uniformly blurring the entire image.
图3:与正常高斯模糊内核的比较。上一行:它显示了所提出的方法。 � 是变换前的高斯, �′ 是变换后的高斯。由于不同的变换可以应用于不同的高斯,我们可以根据场景选择性地模糊图像;它只能模糊场景的前部。底行:它显示了一个正常的高斯模糊内核,它不能以不同的方式处理图像的不同部分,从而均匀地模糊整个图像。
3.2.2Modelling
Following the above mentioned motivation, we learn to deblur by transforming the geometry of the 3D Gaussians. The geometry of the 3D Gaussians is expressed through the covariance matrix, which can be decomposed into the rotation and scaling factors as mentioned in Eq. 3. Therefore, our target is to change the rotation and scaling factors of 3D Gaussians in such a way that we can model the blurring phenomenon. To do so, we have employed an MLP that takes the position �, rotation �, scale �, and viewing direction � of 3D Gaussians as inputs, and outputs (��,��), as given by:
根据上述动机,我们学习通过变换3D高斯的几何形状来解模糊。3D高斯的几何形状通过协方差矩阵来表示,协方差矩阵可以分解为旋转和缩放因子,如等式2中所述。3.因此,我们的目标是改变3D高斯的旋转和缩放因子,以便我们可以对模糊现象进行建模。为此,我们采用了MLP,该MLP将3D高斯的位置 � 、旋转 � 、缩放 � 和观看方向 � 作为输入,并输出 (��,��) ,如下所示:
| (��,��)=ℱ�(�(�),�,�,�(�)), | (6) |
where ℱ� denotes the MLP, and � denotes the positional encoding which is defined as:
其中 ℱ� 表示MLP,并且 � 表示位置编码,其被定义为:
| �(�)=(sin(2���),cos(2���))�=0�−1, | (7) |
where � is the number of the frequencies, and the positional encoding is applied to each element of the vector � [23].
其中 � 是频率的数量,并且位置编码被应用于矢量 � [ 23]的每个元素。
The minima of these scaling factors (��,��) are clipped to 1 and element-wisely multiplied to � and �, respectively, to obtain the transformed attributes �′=�⋅�� and �′=�⋅��. With these transformed attributes, we can construct the transformed 3D Gaussians �(�,�′,�′), which is optimized during training to model the scene blurriness. As �′ is greater than or equal to �, each 3D Gaussian of �(�,�′,�′) has greater statistical dispersion than the original 3D Gaussian �(�,�,�). With the expanded dispersion of 3D Gaussian, it can represent the interference of the neighboring information which is a root cause of defocus blur. In addition, �(�,�′,�′) can model the blurry scene more flexibly as per-Gaussian �� and �� are estimated. Defocus blur is spatially-varying, which implies different regions has different levels of blurriness. The scaling factors for 3D Gaussians that are responsible for a region with harsh defocus blur where various neighboring information in wide range is involved in, becomes bigger to better model high degree of blurriness. Those for 3D Gaussians on the sharp area, on the other hand, are closer to 1 so that they have smaller dispersion and do not represent the influence of the nearby information.
将这些缩放因子 (��,��) 的最小值剪切为1,并分别逐元素地乘以 � 和 � ,以获得变换后的属性 �′=�⋅�� 和 �′=�⋅�� 。利用这些变换后的属性,我们可以构建变换后的3D高斯模型 �(�,�′,�′) ,该模型在训练过程中进行了优化,以对场景模糊度进行建模。由于 �′ 大于或等于 � ,所以 �(�,�′,�′) 的每个3D高斯具有比原始3D高斯 �(�,�,�) 更大的统计离散度。利用三维高斯分布的扩展色散特性,可以表征导致离焦模糊的一个根本原因--相邻信息的干扰。此外, �(�,�′,�′) 可以更灵活地对模糊场景进行建模,因为估计了每高斯 �� 和 �� 。散焦模糊是空间变化的,这意味着不同的区域具有不同的模糊程度。 用于3D高斯的缩放因子(其负责其中涉及宽范围内的各种相邻信息的具有严重散焦模糊的区域)变得更大,以更好地对高度模糊进行建模。另一方面,尖锐区域上的3D高斯的那些更接近于1,使得它们具有较小的色散并且不代表附近信息的影响。
At the time of inference, we use �(�,�,�) to render the sharp images. As mentioned earlier, we assume that multiplying two different scaling factors to transform the geometry of 3D Gaussians can work as blur kernel and convolution in eq. 1. Thus, �(�,�,�) can produce the images with clean and fine details. It is worth noting that since any additional scaling factors are not used to render the images at testing time, �� is not activated so all steps required for the inference of Deblurring 3D-GS are identical to 3D-GS, which in turn enables real-time sharp image rendering. In terms of training, only forwarding �� and simple element-wise multiplication are extra cost.
在推理时,我们使用 �(�,�,�) 来渲染清晰的图像。如前所述,我们假设将两个不同的缩放因子相乘以变换3D高斯的几何形状可以用作等式中的模糊核和卷积。1.因此, �(�,�,�) 可以产生具有清晰和精细细节的图像。值得注意的是,由于在测试时不使用任何额外的缩放因子来渲染图像,因此没有激活 �� ,因此去模糊3D-GS的推理所需的所有步骤与3D-GS相同,这反过来又实现了实时清晰图像渲染。在训练方面,只有转发 �� 和简单的元素乘法是额外的成本。
3.2.3Selective blurring 3.2.3选择性模糊
The proposed method can handle the training images arbitrarily blurred in various parts of the scene. Since we predict (��,��) for each Gaussian, we can selectively enlarge the covariances of Gaussians where the parts in the training images are blurred. Such transformed per-Gaussian covariance is projected to 2D space and it can act as pixel-wise blur kernel at the image space. It is noteworthy that applying different shapes of blur kernels to different pixels plays a pivotal role in modeling scene blurriness since blurriness spatially varies. This flexibility enables us to effectively implement deblurring capability in 3D-GS. On the other hand, a naive approach to blurring the rendered image is simply to apply a Gaussian kernel. As shown in Fig. 3, this approach will blur the entire image, not blur pixel-wisely, resulting in blurring parts that should not be blurred for training the model. Even if learnable Gaussian kernel is applied, optimizing the mean and variance of the Gaussian kernel, a single type of blur kernel is limited in its expressivity to model the complicatedly blurred scene and is optimized to model the average blurriness of the scene from averaging loss function which fails to model blurriness morphing in each pixel. Not surprisingly, the Gaussian blur is a special case of the proposed method. If we predict one (��) for all 3D Gaussians, then it will similarly blur the whole image.
该方法可以处理训练图像在场景的各个部分任意模糊。由于我们为每个高斯预测 (��,��) ,因此我们可以选择性地放大高斯的协方差,其中训练图像中的部分是模糊的。这种变换的每高斯协方差被投影到2D空间,并且它可以充当图像空间处的逐像素模糊核。值得注意的是,将不同形状的模糊核应用于不同像素在建模场景模糊中起着关键作用,因为模糊度在空间上变化。这种灵活性使我们能够在3D-GS中有效地实现去模糊功能。另一方面,模糊渲染图像的简单方法是简单地应用高斯核。如图3所示,这种方法将模糊整个图像,而不是模糊像素,导致模糊不应该模糊训练模型的部分。 即使应用可学习的高斯核,优化高斯核的均值和方差,单一类型的模糊核在其表现力方面也受限于对复杂模糊场景进行建模,并且被优化以根据平均损失函数对场景的平均模糊度进行建模,该平均损失函数未能对每个像素中的模糊度变形进行建模。毫不奇怪,高斯模糊是所提出的方法的特殊情况。如果我们为所有3D高斯模型预测一个 (��) ,那么它同样会模糊整个图像。
Algorithm 1 Add Extra Points
算法1添加额外点
𝒫 :从SfM计算的点云
� :要查找的相邻点的数量
�� :要生成的附加点数
�� :新点和现有点之间的最小所需距离
�add ←GenerateRandomPoints( 𝒫,�� )▷ Uniformly sample �� points
▷ 均匀采样 �� 点
对于 �add 中的每个 � ,
𝒫knn ←FindNearestNeighbors( 𝒫,�,� )▷ Get � nearest points of � from 𝒫
▷ 从 𝒫 获取 � 的 � 最近点
𝒫valid← CheckDistance( 𝒫knn , � , �� )▷ Discard irrelevant neighbors
▷ 丢弃不相关的邻居
��← LinearInterpolate( 𝒫valid , � )▷ Linearly interpolate neighboring colors
▷ 线性插值相邻颜色
AddToPointCloud( 𝒫,�,�� )
3.3Compensation for Sparse Point Cloud
3.3稀疏点云的补偿
3D-GS [15] constructs multiple 3D Gaussians from point clouds to model 3D scenes, and its reconstruction quality heavily relies on the initial point clouds. Point clouds are generally obtained from the structure-from-motion (SfM) [36], which extracts features from multi-view images and relates them to several 3D points. However, it can produce only sparse point clouds if the given images are blurry due to the challenge of feature extraction from blurry inputs. Even worse, if the scene has a large depth of field, which is prevalent in defocus blurry scenes, SfM hardly extracts any points that lie on the far end of the scene. To make a dense point cloud, we add additional points after ��� iterations. �� points are sampled from an uniform distribution �(�,�) where � and � are the minimum and maximum value of the position of the points from the existing point cloud, respectively. The color for each new point � is assigned with the interpolated color �� from the nearest neighbors 𝒫knn among the existing points using K-Nearest-Neigbhor (KNN) [29]. We discard the points whose distance to the nearest neighbor exceeds the distance threshold �� to prevent unnecessary points from being allocated to the empty space. The process of adding extra points to the given point cloud is summarized in algorithm 1. fig. 5 shows that a point cloud with additional points has a dense distribution of points to represent the objects.
3D-GS [ 15]从点云构建多个3D高斯模型来建模3D场景,其重建质量严重依赖于初始点云。点云通常从运动恢复结构(SfM)[ 36]中获得,该方法从多视图图像中提取特征并将其与多个3D点相关联。然而,如果给定的图像由于从模糊输入中提取特征的挑战而模糊,则它只能产生稀疏的点云。更糟糕的是,如果场景具有大的景深,这在散焦模糊场景中很普遍,SfM几乎无法提取位于场景远端的任何点。为了生成密集的点云,我们在 ��� 次迭代后添加额外的点。从均匀分布 �(�,�) 中采样 �� 点,其中 � 和 � 分别是来自现有点云的点的位置的最小值和最大值。 每个新点 � 的颜色使用K-最近邻-Neigbhor(KNN)[ 29]从现有点中的最近邻 𝒫knn 分配插值颜色 �� 。我们丢弃到最近邻的距离超过距离阈值 �� 的点,以防止不必要的点被分配到空白空间。在算法1中总结了向给定点云添加额外点的过程。图5示出了具有附加点的点云具有密集的点分布以表示对象。
Furthermore, 3D-GS [15] effectively manages the number of 3D Gaussians (the number of points) through periodic adaptive density control, densifying and pruning 3D Gaussians. To compensate for the sparsity of 3D Gaussians lying on the far end of the scene, we prune 3D Gaussians depending on their positions. As the benchmark Deblur-NeRF dataset [22] consists of only forward-facing scenes, the z-axis value of each point can be a relative depth from any viewpoints. As shown in fig. 4, we prune out less 3D Gaussians placed on the far edge of the scene to preserve more points located at the far plane, relying on the relative depth. Specifically, the pruning threshold �� is scaled by �� to 1.0 depending on the relative depth, and the lowest threshold is applied to the farthest point. Densifying more for far-plane-3D Gaussians is also an available option, but excessive compensation hinders modeling the scene blurriness, and it can further degrade real-time rendering as extra computational cost is required. We empirically found that flexible pruning was enough to compensate for sparse point cloud, considering the rendering speed. fig. 6 shows that relative depth-based pruning preserves the points lying on the far plane of the scene and leads to successful reconstruction of the objects on the far plane.
此外,3D-GS [ 15]通过周期性自适应密度控制,加密和修剪3D高斯模型,有效地管理3D高斯模型的数量(点数)。为了补偿位于场景远端的3D高斯的稀疏性,我们根据它们的位置修剪3D高斯。由于基准Deburl-NeRF数据集[ 22]仅由前向场景组成,因此每个点的z轴值可以是来自任何视点的相对深度。如图4所示,我们修剪掉放置在场景远边缘的较少3D高斯,以保留位于远平面的更多点,这取决于相对深度。具体地,取决于相对深度,修剪阈值 �� 被缩放 �� 至1.0,并且最低阈值被应用于最远点。 为远平面3D高斯模型增加密度也是一个可用的选项,但过度的补偿会阻碍场景模糊的建模,并且由于需要额外的计算成本,它会进一步降低实时渲染。我们的经验发现,灵活的修剪是足够的,以补偿稀疏点云,考虑到渲染速度。图6示出了基于相对深度的修剪保留了位于场景的远平面上的点,并导致远平面上的对象的成功重建。

Figure 4:Comparison to pruning 3D Gaussians. Left: Given 3D Gaussians. Middle: Applying pruning method proposed by 3D-GS which removes 3D Gaussians with the single threshold (��). Right: Our pruning method which discards unnecessary 3D Gaussians with different thresholds based upon their depth.
图4:与修剪3D高斯曲线的比较。左:给定3D高斯。中间:应用由3D-GS提出的修剪方法,其利用单个阈值( �� )去除3D高斯。右:我们的修剪方法,根据深度丢弃具有不同阈值的不必要的3D高斯。
4Experiments 4实验
Table 1:Quantitative results on real defocus dataset. We color each cell as best and second best. *3D-GS achieved the highest FPS because it failed to model the blurry scene, abnormally small number of 3D Gaussians are in use which in turn raises FPS.
表1:真实的散焦数据集的定量结果。我们将每个单元格着色为最佳和次佳。*3D-GS实现了最高的FPS,因为它无法对模糊场景进行建模,使用的3D高斯数量异常少,这反过来又提高了FPS。
| Cake 蛋糕 | Caps 帽 | Cisco 思科 | Coral 珊瑚 | Cupcake 纸杯蛋糕 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | ||||
| NeRF [23] | 24.42 | 0.7210 | 22.73 | 0.6312 | 20.72 | 0.7217 | 19.81 | 0.5658 | 21.88 | 0.6809 | |||
| 3D-GS [15] | 20.16 | 0.5903 | 19.08 | 0.4355 | 20.01 | 0.6931 | 19.50 | 0.5519 | 21.53 | 0.6794 | |||
| Deblur-NeRF [22] | 26.27 | 0.7800 | 23.87 | 0.7128 | 20.83 | 0.7270 | 19.85 | 0.5999 | 22.26 | 0.7219 | |||
| DP-NeRF [19] | 26.16 | 0.7781 | 23.95 | 0.7122 | 20.73 | 0.7260 | 20.11 | 0.6107 | 22.80 | 0.7409 | |||
| PDRF-10 [28] | 27.06 | 0.8032 | 24.06 | 0.7102 | 20.68 | 0.7239 | 19.61 | 0.5894 | 22.95 | 0.7421 | |||
| Ours | 27.08 | 0.8076 | 24.68 | 0.7437 | 21.06 | 0.7409 | 20.24 | 0.5617 | 22.65 | 0.7477 | |||
| Cups 杯 | Daisy 黛西 | Sausage 香肠 | Seal 密封 | Tools 工具 | Average 平均 | FPS | |||||||
| PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | ↑ | |
| NeRF [23] | 25.02 | 0.7581 | 22.74 | 0.6203 | 17.79 | 0.4830 | 22.79 | 0.6267 | 26.08 | 0.8523 | 22.40 | 0.6661 | < 1 |
| 3D-GS [15] | 20.55 | 0.6459 | 20.96 | 0.6004 | 17.83 | 0.4718 | 22.25 | 0.5905 | 23.82 | 0.805 | 20.57 | 0.6064 | 788* |
| Deblur-NeRF [22] | 26.21 | 0.7987 | 23.52 | 0.6870 | 18.01 | 0.4998 | 26.04 | 0.7773 | 27.81 | 0.8949 | 23.46 | 0.7199 | < 1 |
| DP-NeRF [19] | 26.75 | 0.8136 | 23.79 | 0.6971 | 18.35 | 0.5443 | 25.95 | 0.7779 | 28.07 | 0.8980 | 23.67 | 0.7299 | < 1 |
| PDRF-10 [28] | 26.39 | 0.8066 | 24.49 | 0.7426 | 18.94 | 0.5686 | 26.36 | 0.7959 | 28.00 | 0.8995 | 23.85 | 0.7382 | < 1 |
| Ours | 26.26 | 0.8240 | 23.70 | 0.7268 | 18.74 | 0.5539 | 26.25 | 0.8197 | 27.58 | 0.9037 | 23.82 | 0.7430 | 620 |
Table 2:Quantitative results on synthetic defocus dataset. We color each cell as best and second best. *3D-GS achieved the highest FPS because it failed to model the blurry scene, abnormally small number of 3D Gaussians are in use which in turn raises FPS.
表2:合成散焦数据集的定量结果。我们将每个单元格着色为最佳和次佳。*3D-GS实现了最高的FPS,因为它无法对模糊场景进行建模,使用的3D高斯数量异常少,这反过来又提高了FPS。
| Cozyroom 舒适的房间 | Factory 工厂 | Pool 池 | Tanabata 七夕 | Trolley 小车 | Average 平均 | FPS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | PSNR↑ | SSIM↑ | ↑ | |
| NeRF [23] | 30.03 | 0.8926 | 25.36 | 0.7847 | 27.77 | 0.7266 | 23.90 | 0.7811 | 22.67 | 0.7103 | 25.93 | 0.7791 | < 1 |
| 3D-GS [15] | 30.09 | 0.9024 | 24.52 | 0.8057 | 20.14 | 0.4451 | 23.08 | 0.7981 | 22.26 | 0.7400 | 24.02 | 0.7383 | 789* |
| Deblur-NeRF [22] | 31.85 | 0.9175 | 28.03 | 0.8628 | 30.52 | 0.8246 | 26.26 | 0.8517 | 25.18 | 0.8067 | 28.37 | 0.8527 | < 1 |
| DP-NeRF [19] | 32.11 | 0.9215 | 29.26 | 0.8793 | 31.44 | 0.8529 | 27.05 | 0.8635 | 26.79 | 0.8395 | 29.33 | 0.8713 | < 1 |
| PDRF-10 [28] | 32.29 | 0.9305 | 30.90 | 0.9138 | 30.97 | 0.8408 | 28.18 | 0.9006 | 28.07 | 0.8799 | 30.08 | 0.8931 | < 1 |
| Ours | 32.03 | 0.9269 | 29.89 | 0.9096 | 30.50 | 0.8344 | 27.56 | 0.9071 | 27.18 | 0.8755 | 29.43 | 0.8907 | 663 |
We compared our method against the state-of-the-art deblurrig approaches in neural rendering: Deblur-NeRF [22], DP-NeRF [20], PDRF [28] and original 3D Gaussians Splatting (3D-GS) [15]
我们将我们的方法与神经渲染中最先进的去模糊方法进行了比较:Deflur-NeRF [ 22],DP-NeRF [ 20],PDRF [ 28]和原始的3D高斯飞溅(3D-GS)[ 15]
4.1Experimental Settings 4.1实验设置
We utilized PyTorch [27] to create our deblurring pipeline while maintaining the differentiable Gaussian rasterization 3D-GS [15]. We conducted 30k iterations of training. Adam optimizer [16] is used for optimization with the identical setting of 3D-GS. We set the learning rate for MLP at 1e-3, and the rest parameters are identical to 3D-GS. We use MLP with 3 hidden layers, each layer having 64 hidden units and ReLU activation. MLP is initialized with Xavier intialization [11]. For adding extra points to compensate the sparse point cloud, we set the addition start iteration ��� to 2,500, the number of supplementing points �� to 100,000, the number of neighbors � to 4, and the minimum distance threshold �� to 10. In terms of depth-based pruning, �� for pruning threshold is set to 5e-3 and 0.3 is used for ��, the pruning threshold scaler. All the experiments were conducted on NVIDIA RTX 4090 GPU with 24GB memory.
我们利用PyTorch [ 27]创建去模糊流水线,同时保持可微分高斯光栅化3D-GS [ 15]。我们进行了3万次迭代训练。Adam优化器[ 16]用于与3D-GS相同设置的优化。我们将MLP的学习率设置为1 e-3,其余参数与3D-GS相同。我们使用带有3个隐藏层的MLP,每个层有64个隐藏单元和ReLU激活。MLP使用Xavier初始化进行初始化[ 11]。为了添加额外点以补偿稀疏点云,我们将添加开始迭代 ��� 设置为2,500,将补充点 �� 的数量设置为100,000,将相邻点 � 的数量设置为4,并且将最小距离阈值 �� 设置为10。在基于深度的修剪方面,用于修剪阈值的 �� 被设置为5e-3,并且0.3被用于 �� ,修剪阈值缩放器。所有的实验都是在具有24 GB内存的NVIDIA RTX 4090 GPU上进行的。
We evaluated the performance on the benchmark Deblur-NeRF dataset [22] that includes both synthetic and real defocus blurred images. This dataset contains five scenarios in the synthetic defocus category and ten in the real defocus category. Synthetic defocus images are constructed using Blender [5]. By setting the aperture size and randomly selecting a focal plane between the closest and farthest depths, realistic defocus blur effects were produced. COLMAP [36, 37] is used to calculate the camera position of the blur and reference image in the real scene after choosing a big aperture to capture the defocus image.
我们评估了基准Deflur-NeRF数据集[ 22]的性能,该数据集包括合成和真实的散焦模糊图像。该数据集包含合成散焦类别中的五个场景和真实的散焦类别中的十个场景。合成散焦图像使用Blender构建[ 5]。通过设置光圈大小和随机选择最近和最远深度之间的焦平面,产生逼真的散焦模糊效果。COLMAP [ 36,37]用于在选择大光圈捕获散焦图像后计算真实的场景中模糊和参考图像的相机位置。

Figure 5:Comparison on densifying point clouds during training. Left: Example training view. Middle: Point cloud at 5,000 training iterations without adding points. Bottom: Point cloud at 5,000 training iterations with adding extra points at 2,500 iterations.
图5:训练过程中点云加密的比较。左:示例训练视图。中图:5,000次训练迭代的点云,不添加点。底部:5,000次训练迭代的点云,在2,500次迭代时添加额外的点。
4.2Results and Comparisons
4.2结果和比较
In this section, we provide the outcomes of our experiments, presenting a thorough analysis of both qualitative and quantitative results. Our evaluation framework encompasses a diverse set of metrics to show a comprehensive assessment of the experimental results. Primarily, we rely on established metrics such as the Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Frames Per Second (FPS).
在本节中,我们提供了我们的实验结果,对定性和定量结果进行了全面的分析。我们的评估框架包括一组不同的指标,以显示对实验结果的全面评估。首先,我们依赖于已建立的指标,如峰值信噪比(PSNR),结构相似性指数(SSIM)和每秒帧数(FPS)。
First of all, we show the transformation in the values of two Gaussian attributes (scale and rotation) to model the blur. The average values of these two attributes have been mentioned in Table 3. These values have been computed for all the scenes in real defocus dataset. It can be seen that during training, as compared to testing, 3D Gaussians of larger values of scale and rotation have been used to rasterize the scene. This indicates that larger values of scale and rotation are needed to adjust the 3D Gaussians to rasterize the blurred (training) images. While, in contrast, smaller values of these two attributes demonstrate that the smaller sized Gaussians are more suitable to model the fine details that are present in the sharp (testing) images.
首先,我们展示了两个高斯属性(缩放和旋转)的值的变换来对模糊进行建模。这两个属性的平均值已在表3中提及。这些值已被计算的所有场景在真实的散焦数据集。可以看出,在训练期间,与测试相比,具有较大尺度和旋转值的3D高斯模型已被用于对场景进行光栅扫描。这表明需要更大的缩放和旋转值来调整3D高斯以使模糊(训练)图像光栅化。相反,这两个属性的较小值表明较小尺寸的高斯更适合于对清晰(测试)图像中存在的精细细节进行建模。

Figure 6:Comparison on applying depth-based pruning. Top: Rendered image from the model with depth-dependent pruning. Bottom: Rendered image from the model with naive pruning as 3D-GS does.
图6:应用基于深度的修剪的比较。顶部:使用深度相关修剪从模型渲染的图像。下图:从模型中渲染的图像,像3D-GS一样进行朴素修剪。
As shown in table 1 and fig. 1 our method is on par with the state-of-the-art model in PSNR and achieve state-of-the-art performance evaluated under SSIM on the real defocus dataset. At the same time, it can still enjoy real-time rendering, with noticeable FPS, compared to other deblurring models. Also, table 2 shows the quantitative result on the synthetic defocus dataset. FPS of 3D-GS is abnormally high because it fails to model the blurry scene, thus only small number of 3D Gaussians are created. fig. 7 and fig. 8 show the qualitative results on real and synthetic defocus dataset, respectively. We can see that ours can produce sharp and fine details, while 3D-GS fail to reconstruct those details.
如表1和图1所示,我们的方法在PSNR方面与最先进的模型相当,并且在真实的散焦数据集上实现了在SSIM下评估的最先进的性能。与此同时,与其他去模糊模型相比,它仍然可以享受实时渲染,具有明显的FPS。此外,表2示出了关于合成散焦数据集的定量结果。3D-GS的FPS异常高,因为它无法对模糊场景进行建模,因此只能创建少量的3D高斯。图7和图8分别示出了关于真实的和合成散焦数据集的定性结果。我们可以看到,我们可以产生清晰和精细的细节,而3D-GS无法重建这些细节。
4.3Ablation Study 4.3消融研究
4.3.1Extra points allocation
4.3.1额外积分分配
In this section, we evaluate the effect of adding extra points to the sparse point cloud. As shown in fig. 5, directly using sparse point cloud without any point densification only represents the objects with a small number of points or totally fails to model the tiny objects. Meanwhile, in case extra points are added to the point cloud, points successfully represent the objects densely. Also, the quantitative result is presented in table 4. It shows assigning valid color features to the additional points is important to deblur the scene and reconstruct the fine details.
在本节中,我们将评估向稀疏点云添加额外点的效果。如图5所示,直接使用稀疏点云而不进行任何点加密只能表示具有少量点的对象,或者完全无法对微小对象进行建模。同时,在向点云添加额外点的情况下,点成功地密集地表示对象。此外,定量结果见表4。这表明为额外的点分配有效的颜色特征对于去模糊场景和重建细节是重要的。
Figure 7:Qualitative results on real defocus blur dataset.
图7:真实的散焦模糊数据集的定性结果。

Figure 8:Qualitative results on synthetic defocus blur dataset.
图8:合成散焦模糊数据集的定性结果。
4.3.2Depth-based pruning 4.3.2基于深度的剪枝
We conduct an ablation study on depth-based pruning. To address excessive sparsity of point cloud at the far plane, we prune the points on the far plane less to maintain more numbers of points. table 5 shows there is severe rendering quality degradation if naive pruning, prunes the points with the same threshold from near plane to far plane, is used. In addition, fig. 6 shows a failure to reconstruct objects at the far plane when naive pruning is used, while objects lying on the near-end of the scene are well reconstructed. Meanwhile, ours, with depth-based pruning, can render clean objects on both near and far planes.
我们对基于深度的修剪进行了消融研究。为了解决点云在远平面上过于稀疏的问题,我们对远平面上的点进行较少的修剪,以保持更多的点。表5示出了如果使用朴素修剪(从近平面到远平面用相同阈值修剪点),则存在严重的渲染质量降级。此外,图6示出了当使用朴素修剪时在远平面处重建对象的失败,而位于场景的近端的对象被很好地重建。同时,我们的,基于深度的修剪,可以在近平面和远平面上渲染干净的对象。
Table 3:Transformation of two attributes (scale and rotaion) of 3D Gaussians to model the blur.
表3:3D高斯的两个属性(比例和旋转)的变换以对模糊进行建模。
| train 火车 | test 测试 | |
|---|---|---|
| scale 规模 | 0.87 | 0.85 |
| rotation 旋转 | 0.26 | 0.25 |
Table 4:Ablation study on adding the extra points. w/ Random Colors stands for uniformly allocating points to the point cloud but color features are randomly initialized, rather than interpolated from neighboring points.
表4:增加额外点的消融研究。w/ Random Colors表示将点均匀分配给点云,但颜色特征是随机初始化的,而不是从相邻点插值。
| Methods 方法 | PSNR ↑ | SSIM ↑ |
|---|---|---|
| w/o Extra Points 无额外积分 | 22.56 | 0.7016 |
| w/ Random Colors w/随机颜色 | 22.90 | 0.7089 |
| w/ Extra Points w/额外积分 | 23.80 | 0.7430 |
Table 5:Ablation study on depth-depending pruning. Naive pruning stands for using naive points pruning from 3D-GS and Depth-based pruning stands for applying our depth-based pruning.
表5:对深度依赖性修剪的消融研究。朴素修剪代表使用来自3D-GS的朴素点修剪,基于深度的修剪代表应用我们的基于深度的修剪。
| Methods 方法 | PSNR ↑ | SSIM ↑ |
|---|---|---|
| Naive pruning 朴素剪枝 | 23.33 | 0.7296 |
| Depth-based pruning 基于深度的剪枝 | 23.80 | 0.7430 |
5Limitations & Future Works
5局限与未来作品
NeRF-based deblurring methods [22, 20, 28], which are developed under the assumption of volumetric rendering, are not straightforwardly applicable to rasterization-based 3D-GS [15]. However, they can be compatible to rasterization by optimizing their MLP to deform kernels in the space of the rasterized image instead of letting MLP deform the rays and kernels in the world space. Although it is an interesting direction, it will incur additional costs for interpolating pixels and just implicitly transform the geometry of 3D Gaussians. Therefore, we believe that it will not be an optimal way to model scene blurriness using 3D-GS [15]. Another approach to deblur the defocus blur using 3D-GS [15] can be convolving the rasterized image with conventional grid blur kernels such as gaussian blur kernel [14]. With this approach however, the kernel expressivity is limited compared to the learnable kernels since the Gaussian blur kernel is a simple unimodal Gaussian distribution along each axis and is not learnable. Instead of a fixed Gaussian blur kernel, adopting a learnable grid blur kernel can also be another promising direction to address defocus blur. Nevertheless, as blurriness naturally varies spatially across the scene and each pixel, it is ideal to train blur kernels for every pixel from all training views. Thus, such method can incur high memory requirements, and its usage is limited if the rendering image is high resolution or lots of training images are provided.
基于NeRF的去模糊方法[ 22,20,28]是在体积渲染的假设下开发的,并不直接适用于基于光栅化的3D-GS [ 15]。然而,它们可以通过优化它们的MLP以使光栅化图像的空间中的核变形而不是让MLP使世界空间中的射线和核变形来与光栅化兼容。虽然这是一个有趣的方向,但它会产生额外的插值像素成本,并且只是隐式地转换3D高斯的几何形状。因此,我们认为使用3D-GS [ 15]对场景模糊进行建模不是最佳方式。使用3D-GS [ 15]去模糊散焦模糊的另一种方法可以是将光栅化图像与诸如高斯模糊核[ 14]的传统网格模糊核进行卷积。 然而,通过这种方法,与可学习的核相比,核表达能力是有限的,因为高斯模糊核是沿沿着每个轴的简单单峰高斯分布,并且是不可学习的。代替固定的高斯模糊核,采用可学习的网格模糊核也可以是解决散焦模糊的另一个有前途的方向。然而,由于模糊度在场景和每个像素上自然地在空间上变化,因此理想的是为来自所有训练视图的每个像素训练模糊内核。因此,这种方法可能会导致高存储器需求,并且如果渲染图像是高分辨率的或提供大量训练图像,则其使用受到限制。
6Conclusion 6结论
We proposed Deblurring 3D-GS, the first defocus deblurring algorithm for 3D-GS. We adopted a small MLP that transforms the 3D Gaussians to model the scene blurriness. We also further facilitate deblurring by densifying sparse point clouds from blurry input images through additional point allocation, which uniformly distributes points in the scene and assigns color features using the K-Nearest-Neighbor algorithm. Also, as we applied depth-based pruning instead of naive pruning, which 3D-GS has adopted, we could preserve more points at the far edge of the scene where SfM usually struggles to extract features and fails to generate enough points. Through extensive experiments, we validated that our method can deblur the defocus blur while still enjoying the real-time rendering with FPS > 200. This is because we use the MLP only during the training time, and the MLP is not involved in the inference stage, keeping the inference stage identical to the 3D-GS. Our method achieved state-of-the-art performance or performed comparably with current cutting-edge models evaluated under different metrics.
我们提出了第一个3D-GS的散焦去模糊算法Deflurring 3D-GS。我们采用了一个小的MLP转换的3D高斯模型的场景模糊。我们还通过额外的点分配从模糊的输入图像中致密稀疏点云来进一步促进去模糊,该点分配均匀地分布在场景中,并使用K-最近邻算法分配颜色特征。此外,由于我们应用了基于深度的修剪而不是3D-GS采用的朴素修剪,因此我们可以在场景的远边缘保留更多点,而SfM通常难以提取特征并且无法生成足够的点。通过大量的实验,我们验证了我们的方法可以去模糊散焦模糊,同时仍然享受与FPS > 200的实时渲染。这是因为我们仅在训练期间使用MLP,并且MLP不参与推理阶段,从而使推理阶段与3D-GS相同。 我们的方法实现了最先进的性能,或者使用在不同指标下评估的当前尖端模型进行了验证。