原文链接:https://arxiv.org/abs/2402.10739
1. 引言
基于Transformer的点云分析方法有二次时空复杂度,一些方法通过限制感受野降低计算。这引出了一个问题:如何设计方法实现线性复杂度并有全局感受野。
状态空间模型(SSM)作为序列建模方法,Mamba在结构状态空间模型(S4)的基础上使用时变SSM参数和硬件感知算法,实现了线性复杂度和全局感受野。但目前的Mamba较少用于视觉任务。
本文探索SSM在点云分析任务中的潜力。直接使用Mamba的性能不佳,这是因为SSM的单向建模能力(相反,自注意力是输入顺序不变的)。本文提出点状态空间模型(PointMamba),首先生成点的token序列,然后使用重排序策略以特定顺序扫描数据,使模型捕捉点云结构。最后将重排序后点的token输入Mamba编码器,进行全局建模。
实验表明,本文方法可以超过基于Transformer方法的性能,且有更少的参数和计算量。
3. 方法
3.1 准备知识
状态空间模型:状态空间模型建模了时不变(LTI)系统,使用一阶微分方程捕捉系统动态:
h ˙ ( t ) = A h ( t ) + B x ( t ) , y ( t ) = C h ( t ) + D x ( t ) . \dot h(t)=Ah(t)+Bx(t),\\y(t)=Ch(t)+Dx(t). h˙(t)=Ah(t)+Bx(t),y(t)=Ch(t)+Dx(t).
为处理离散token序列输入,需要进行离散化:
h k = A ˉ h k − 1 + B ˉ x k , y k = C ˉ h k + D ˉ x k . h_k=\bar Ah_{k-1}+\bar Bx_k,\\y_k=\bar Ch_k+\bar Dx_k. hk=Aˉhk−1+Bˉxk,yk=Cˉhk+Dˉxk.
其中 A ˉ ∈ R N × N , B ˉ ∈ R N × 1 , C ˉ ∈ R 1 × N , D ˉ ∈ R \bar A\in\mathbb R^{N\times N},\bar B\in\mathbb R^{N\times 1},\bar C\in\mathbb R^{1\times N},\bar D\in\mathbb R Aˉ∈RN×N,Bˉ∈RN×1,Cˉ∈R1×N,Dˉ∈R为参数矩阵。 D ˉ \bar D Dˉ为残差连接,通常可简化或忽略。离散化需要使用时间步长 Δ \Delta Δ,在连续信号 x ( t ) x(t) x(t)进行采样,得到 x k = x ( k Δ ) x_k=x(k\Delta) xk=x(kΔ)。这使得:
A ˉ = ( I − Δ / 2 ⋅ A ) − 1 ( I + Δ / 2 ⋅ A ) , B ˉ = ( I − Δ / 2 ⋅ A ) − 1 Δ B , C ˉ = C \bar A=(I-\Delta/2\cdot A)^{-1}(I+\Delta/2\cdot A),\\\bar B=(I-\Delta/2\cdot A)^{-1}\Delta B,\\\bar C=C Aˉ=(I−Δ/2⋅A)−1(I+Δ/2⋅A),Bˉ=(I−Δ/2⋅A)−1ΔB,Cˉ=C
选择性SSM: B ˉ , C ˉ \bar B,\bar C Bˉ,Cˉ和 Δ \Delta Δ为动态、输入相关的参数,从而使得SSM为时变模型。这样能够过滤和捕捉时间相关的特征和关系,从而更精确地表达输入序列。
3.2 PointMamba
3.2.1 概述
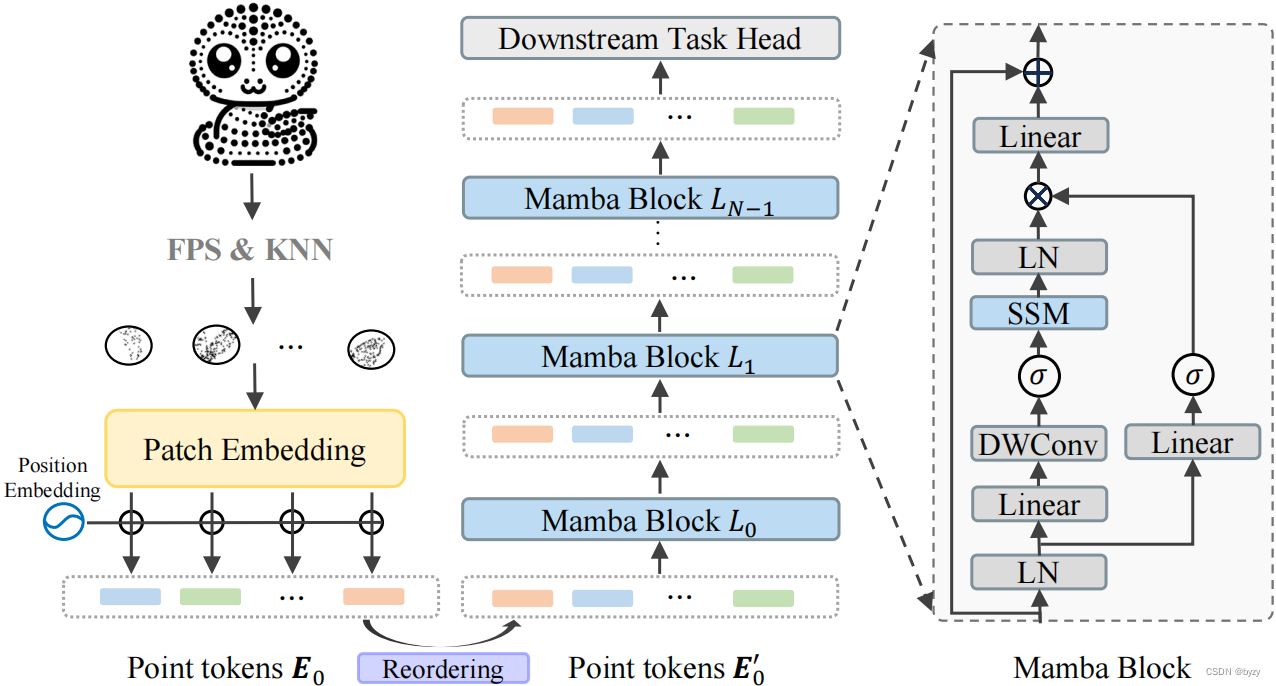
如图所示,本文方法包括点tokenizer,重排序策略、Mamba和下游任务头。本文使用轻量化PointNet嵌入点的patch,得到点的token,然后根据几何坐标进行重排序,将序列长度变为3倍,输入Mamba。
3.2.2 点tokenizer
使用最远点采样(FPS)和K近邻(KNN)算法将点云分为不规则的点patch。具体来说,给定含 M M M个点的点云 I ∈ R M × 3 I\in\mathbb R^{M\times3} I∈RM×3,使用FPS采样 n n n个关键点,然后为每个关键点,使用KNN算法选择 k k k个最近点,得到 n n n个patch P ∈ R n × k × 3 P\in\mathbb R^{n\times k\times3} P∈Rn×k×3。然后,求取patch中各点相对关键点的相对坐标,并使用轻量化PointNet映射到特征空间,得到点token E 0 ∈ R n × C E_0\in\mathbb R^{n\times C} E0∈Rn×C。
3.2.3 重排序策略
由于Mamba是单向处理数据,适合1D数据;但难以处理点云这类无序数据。
本文通过特定顺序扫描点云,以捕捉点云结构。如图所示,本文分别基于点token簇中心的几何 x , y , z x,y,z x,y,z坐标进行排序并拼接,得到 E 0 ′ ∈ R 3 n × C E'_0\in\mathbb R^{3n\times C} E0′∈R3n×C。该方法通过提供更有逻辑的几何扫描顺序,提高了Mamba的几何建模能力。

3.2.4 Mamba块
每个Mamba块包含层归一化(LN)、SSM、逐深度卷积和残差连接,如图1右侧所示。公式表示为:
Z l ′ = D W ( M L P ( L N ( Z l − 1 ) ) ) , Z l = M L P ( L N ( S S M ( σ ( Z l ′ ) ) ) × σ ( L N ( Z l − 1 ) ) ) + Z l − 1 Z'_l=DW(MLP(LN(Z_{l-1}))),\\Z_l=MLP(LN(SSM(\sigma(Z_l')))\times\sigma(LN(Z_{l-1})))+Z_{l-1} Zl′=DW(MLP(LN(Zl−1))),Zl=MLP(LN(SSM(σ(Zl′)))×σ(LN(Zl−1)))+Zl−1
其中 Z l ∈ R 3 n × C Z_l\in\mathbb R^{3n\times C} Zl∈R3n×C为第 l l l块的输出, Z 0 = E 0 ′ Z_0=E'_0 Z0=E0′; σ \sigma σ为SiLU激活函数。
3.2.5 预训练
本文使用PointMAE的设置进行预训练,即随机掩蔽60%的点patch,使用自编码器提取点的特征并使用预测头重建点云。
自编码器可公式化为:
T v = F e ( T v + P E ) , H v , H m = F d ( C o n c a t ( T v , T m ) ) , P m = F h ( H m ) . T_v=F_e(T_v+PE),\\H_v,H_m=F_d(Concat(T_v,T_m)),\\P_m=F_h(H_m). Tv=Fe(Tv+PE),Hv,Hm=Fd(Concat(Tv,Tm)),Pm=Fh(Hm).
其中 F e F_e Fe为编码器,以未掩蔽的token T v T_v Tv为输入; F d F_d Fd为Mamba解码器,以 F e F_e Fe的输出和掩蔽的token T m T_m Tm为输入。本文仅在编码器和解码器的第一层加入位置编码 P E PE PE。 F h F_h Fh为线性层,将掩蔽token H m H_m Hm投影为与掩蔽输入点形状相同的向量。使用Chamfer距离作为重建损失,以恢复掩蔽点的坐标。
4. 实验
4.1 实施细节
与ViT不同,本文不使用类别token。分类时,本文将最后一层Mamba的所有输出平均值用于分类。分割任务则将中间多层的输出合并,进行最大和均值池化得到全局特征,然后与逐点特征拼接,输入线性层预测。
4.2 与基于Transformer的方法比较
实验表明,本文方法在无预训练情况下能达到与基于Transformer的方法相当的性能,且有更少的参数和计算量。预训练和使用重排序策略均能提高性能。
此外,随着序列长度的增加,基于Transformer的方法GPU内存占用显著增加,但本文的PointMamba仅线性增长。
4.3 消融研究
重排序策略:比较不进行重排序(1倍序列长度)、进行重排序(3倍序列长度)和双向重排序(即将重排序结果逆序后与重排序结果拼接,6倍序列长度)。实验表明,基于Transformer的方法在序列长度增加时,性能略微下降;重排序策略能提高单向建模Mamba在点云中的适应能力;进一步增加序列长度能进一步提高性能,但为平衡计算量与性能,本文选择3倍序列长度;尽管如此,由于本文方法的线性复杂度,计算量增长也远小于基于Transformer的方法。
分类token的分析:实验表明,不使用类别token能达到最好的分类性能。
4.4 局限性
预训练没有考虑Mamba的单向建模特点;重排序需要将序列长度变为3倍。