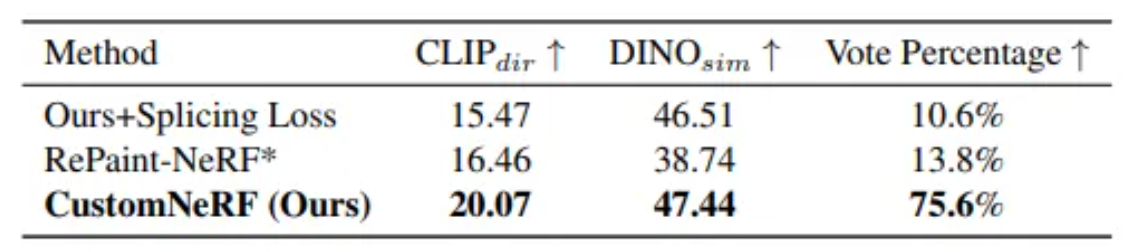
排序
- 1. 复杂度
- 2. 插入排序
- 2.1 直接插入排序
- 2.2 希尔排序
- 3. 选择排序
- 3.1 直接选择排序
- 3.2 堆排序
排序在生活中很常见,比如在网购时,按价格排序,按好评数排序,点餐时,按评分排序等等。而排序有快和慢,快的排序效率高,慢的排序效率低,需要的时间也多。下面就一一介绍各种排序。介绍排序算法时,统一以 升序为例。
1. 复杂度
当一个算法编写完成后,运行时需要消耗时间和空间资源。因此,衡量一个算法的好坏,需要从时间和空间两个维度来衡量,即时间复杂度和空间复杂度。
时间复杂度是衡量快慢的,空间复杂度是衡量该算法运行所需的额外空间。现如今,计算机的内存空间已经很大了,因此空间复杂度已经不是特别关注了。
时间复杂度是一个函数,一个算法的基本操作的执行次数就是该算法的时间复杂度。
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}
}
比如这段代码主要执行的是++count语句,计算该语句的执行次数。
可以看到,++count外套了两层循环,外循环每执行一次,内循环执行N次,而外循环执行了N次,因此++count语句执行了N^2次。算法的执行次数最多的语句一般在循环内部。因此计算时间复杂度,首要计算的就是循环内的。而这个函数可能是若干多项式的和,我们不可能把这个算法的时间复杂度算的非常清楚,只需要知道大概就可以了。因此时间复杂度采用大O渐进表示法。
大O渐进表示法:
1.在这个运行次数的函数中,只保留最高阶的那一项,比如10N^2+2N+2---->10N^2
2.如果最高阶存在并且不是1,那么将该项的系数化为1,比如10N^2 —>N^2
最终我们就得到了一个很简单的函数。此外,有些算法的时间复杂度在不同情况下会有不同,因此需要计算最坏情况和最好情况,有些排序算法就存在这种情况。
空间复杂度也是一个函数,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。空间复杂度计算的是额外使用的空间的大小,不包括本身对变量开辟的空间。
复杂度主要有以下几种
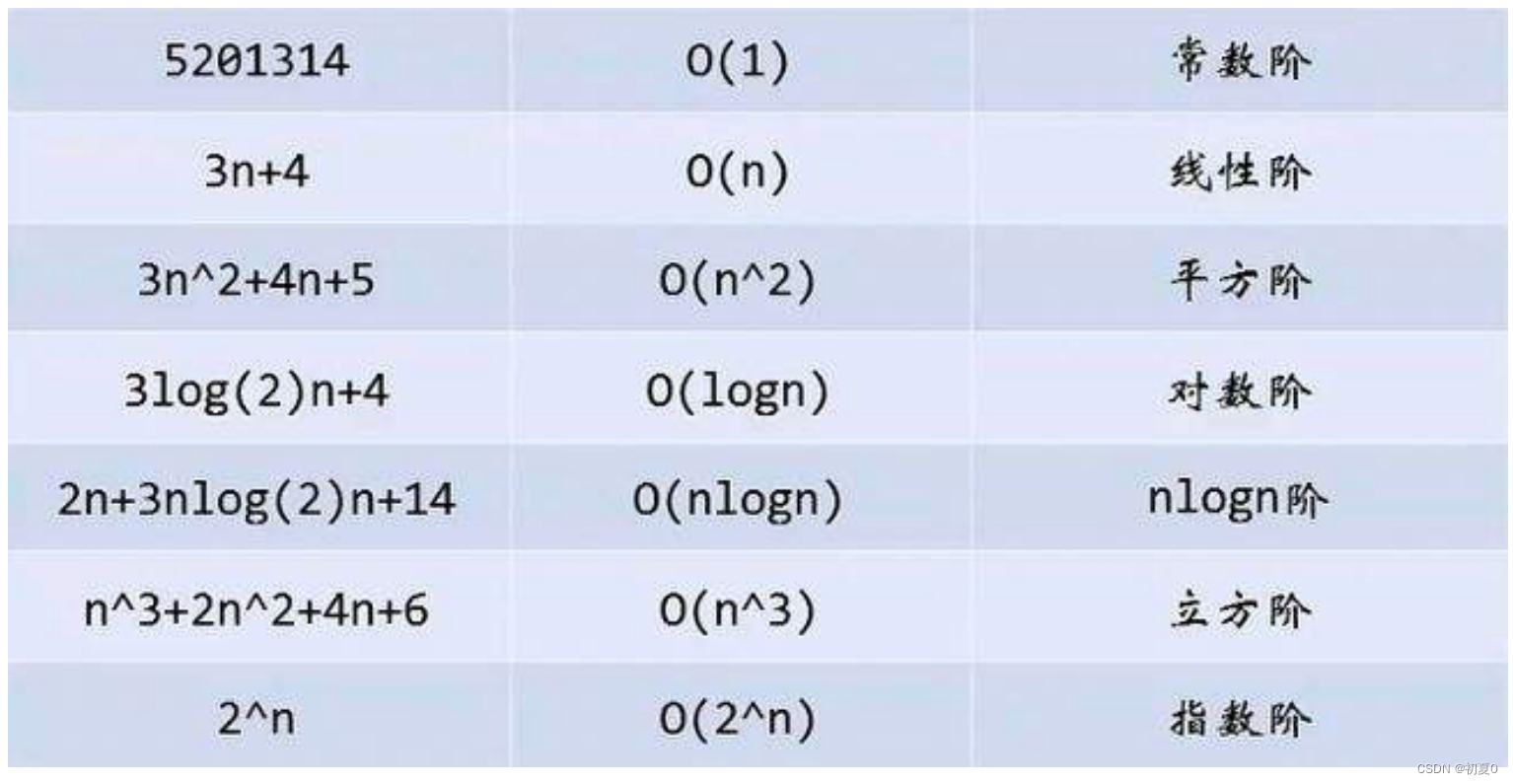
其中含有对数的主要是以2为底数的。
2. 插入排序
2.1 直接插入排序
思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
什么意思呢?我们举一个例子,比如将排序5,9,7,6,2
排序过程如下。
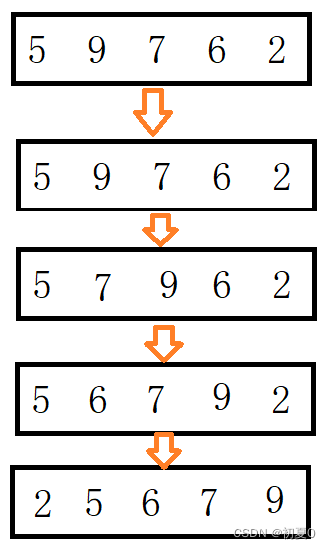
当数组遍历完,得到的就是有序的数组了。
void InsertSort(int* array, int numsArr)//待排序数组和数组大小
{//插入numsArr-1次for (int i = 0; i < numsArr - 1; i++){int end = i;int tmp = array[end + 1];while (end >= 0){//后移if (array[end] > tmp){array[end + 1] = array[end];--end;}else{break;}}array[end + 1] = tmp;}
}
直接插入排序的时间复杂度分最好情况和最坏情况,最好情况是数组本就有序,不需要插入,但是需要遍历一遍数组,所以时间复杂度为O(N);最坏情况是数组逆序,插入的次数是1,2,3,4…N-3,N-2,N-1次,数据是一个等差数列,计算出来为**(N^2-N)/2** 根据大O渐进表示法最终化简为O(N^2);
结论:最坏情况O(N^2)最好情况O(N)
空间复杂度O(1),表示没有用到额外空间。
2.2 希尔排序
希尔排序又称为缩小增量排序,希尔排序对直接插入排序进行了优化,先进行若干次预排序,在进行一次直接插入排序,预排的作用是使得所有记录更快的接近有序。
基本思想是:先选定一个整数(假设为K),把待排序的所有记录分成K个
组,所有距离为K的记录分在同一组内,并对每一组内的记录进行插入排序。然后缩小K的值,重复上述分组和排序的工作。当K=1时,所有记录在一组内排好序。
这里举例将10,9,8,7,6,5,4,3,2,1进行第一轮的排序,假设K=3;
排序过程如图

可以看到,第一轮的排序结果,已经很接近有序了,缩小K的值,在进行分组和排序,当K=1时,所有数据为一组,此时进行的就是直接插入排序。
将数据分组进行预排,可以将更小的数据更快的插入到前面,更大的数据更快的移到后面,减少了插入和移动的次数。
整数的选择也是一个问题,太小了会导致预排效果不明显,太大了会导致预排次数变多,因此整数的每次选取方式为缩小三倍在加1,加1会使得最后一次这个整数一定为1。即最后一次的排序一定是直接插入排序。
代码如下
void ShellSort(int* array, int numsArr)
{int gap = numsArr;while (gap > 1){//间隔gap的数据作为一组,一共gap组//gap=1时是直接插入排序gap = gap / 3 + 1; for (int i = 0; i < numsArr - gap; i++){int end = i;int tmp = array[end + gap];while (end >= 0){//往后挪数据if (array[end] > tmp){array[end + gap] = array[end];end -= gap;}else{break;}}array[end + gap] = tmp;}}
}
希尔排序的时间复杂度比较难算,因为预排和gap的选择会影响结果,并且每一次的预排都会对下一次的预排产生影响。这里直接说结论,希尔排序的时间复杂度大约为N^1.3。
3. 选择排序
3.1 直接选择排序
思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始(或末尾)位置,直到全部待排序的数据元素排完 。
这里进行一个小的优化,同时选出最大和最小的元素,分别放到末尾和起始位置。
但也会产生一个小问题,我们先看代码。
void SelectSort(int* array, int numsArr)
{int begin = 0, end = numsArr - 1;while (begin < end){//最大最小值的下标int minIndex = begin, maxIndex = begin;for (int i = begin + 1; i <= end; i++){//找最小值并更新下标if (array[i] < array[minIndex]){minIndex = i;}//找最大值并更新下标if (array[i] > array[maxIndex]){maxIndex = i;}}swap(&array[begin], &array[minIndex]);//最大值和起始位置重复了if (maxIndex == begin)maxIndex = minIndex;swap(&array[end], &array[maxIndex]);begin++;end--;}
}
问题是会产生数据重复,看下面这组数据。
9,2,3,4,5,6,8,1
如果没有这两条语句会产生什么情况。
if (maxIndex == begin)
maxIndex = minIndex;

当最大值的下标和起始位置的下标重复,就会产生上面的情况,解决办法就是加上判断语句。
时间复杂度:O(N^2)
空间复杂度:O(1)
3.2 堆排序
关于堆排序在之前已经介绍过了,这里就不在赘述了,大家可以看这篇进行了解:堆的应用
代码如下
void HeapSort(int* array, int numsArr)
{//向下调整建堆,复杂度O(N)for (int i = (numsArr - 2) / 2; i >= 0; i--){AdJustDown(array, numsArr, i);}//升序建大堆;降序建小堆//复杂度O(N*logN)int i = numsArr - 1;while (i > 0){swap(&array[0], &array[i]);//交换首尾元素AdJustDown(array, i, 0);i--;}
}
void AdJustDown(int* array, int num_array, int parent)//建大堆
{//假设左孩子符合条件int child = parent * 2 + 1;while (child < num_array){//存在右孩子且右孩子符合条件if (child + 1 < num_array && array[child + 1] > array[child]){++child;}if (array[child] > array[parent]){//交换数据swap(&array[child], &array[parent]);//更新下标parent = child;child = parent * 2 + 1;}else{break;}}
}
这里对堆排序的时间复杂度进行一个计算。
如下图,这是建堆的时间复杂度
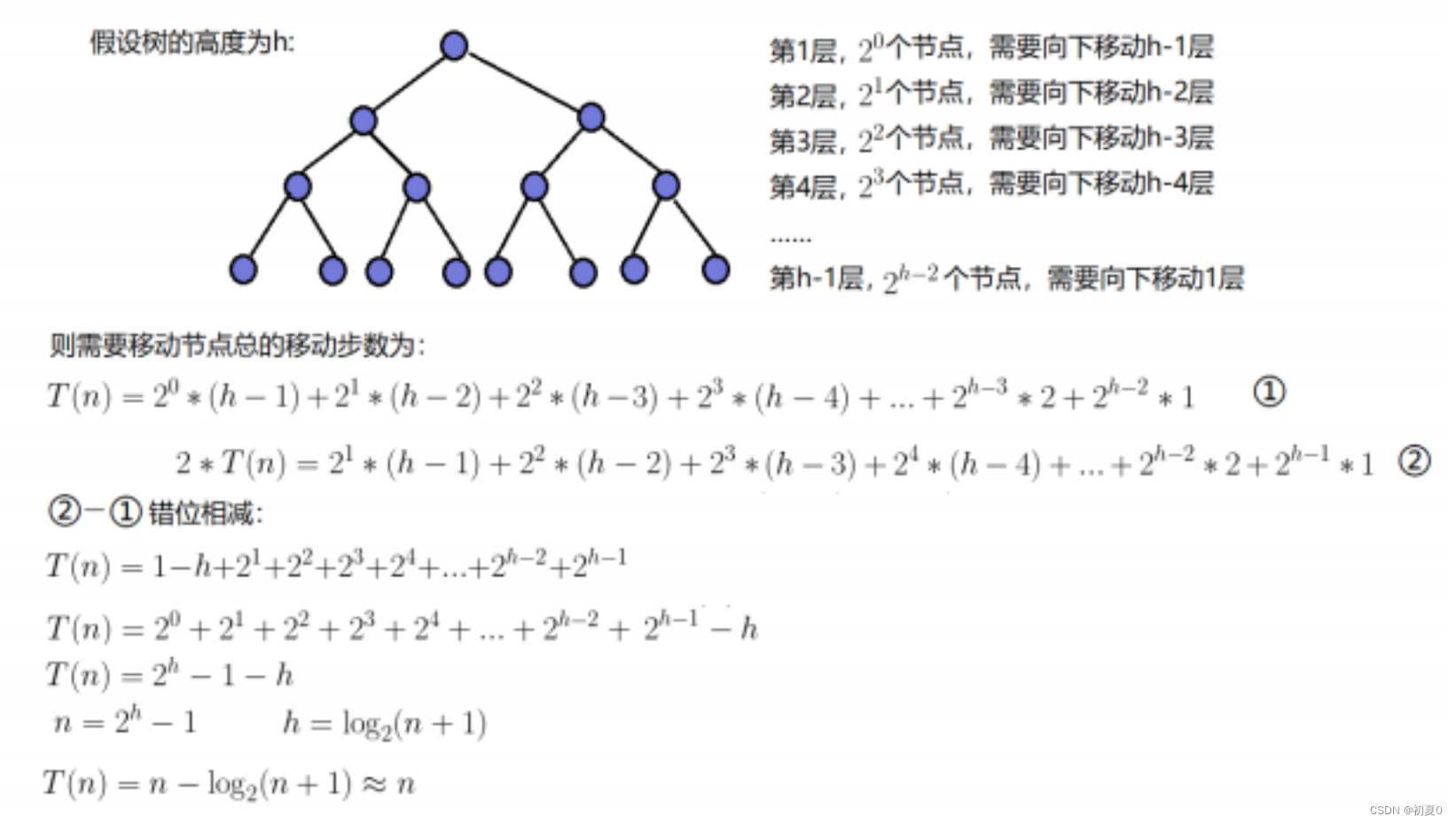
根据大O渐进表示法,最终建堆的时间复杂度为O(N)
而进行排序时,时间复杂度为
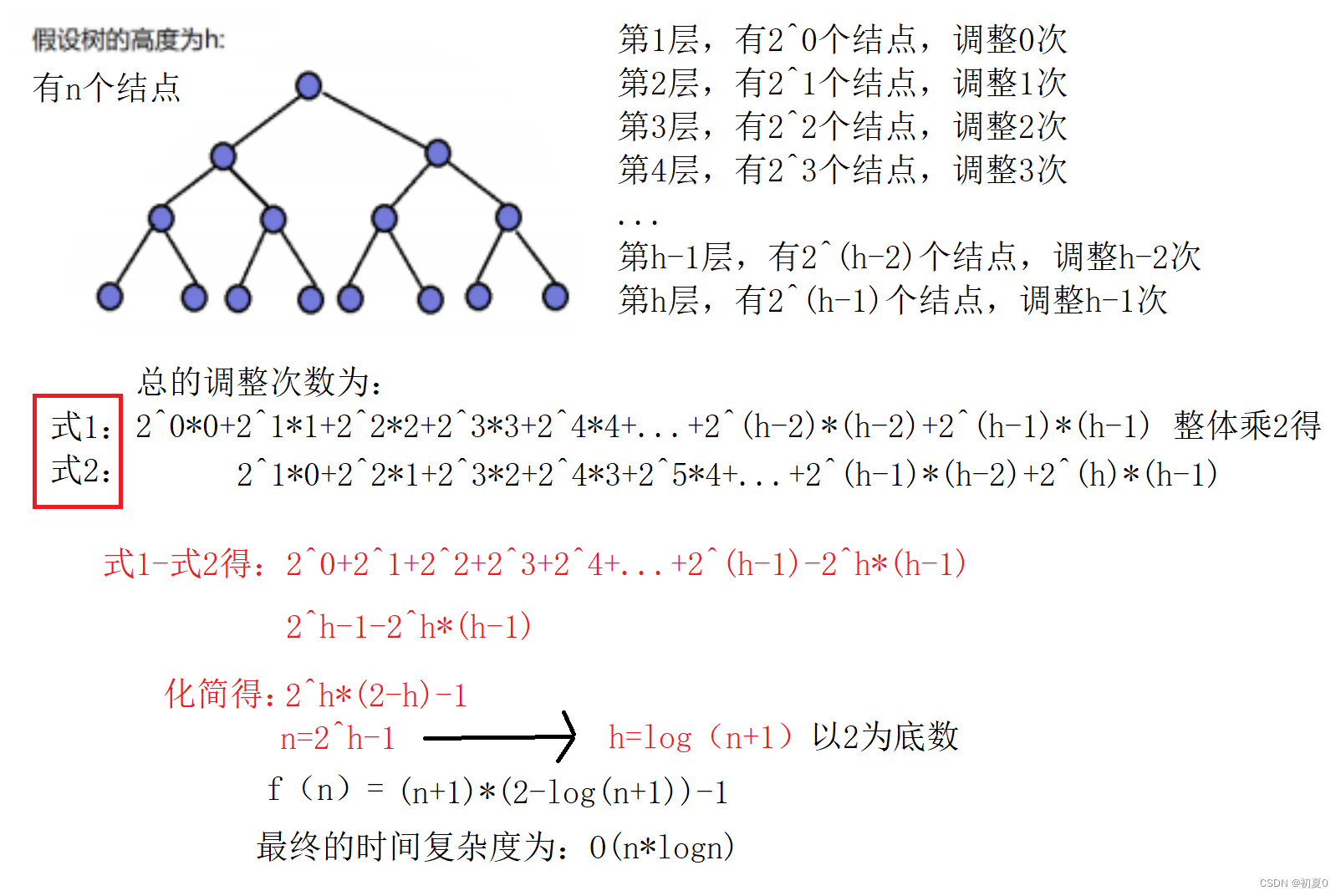
建堆的时间复杂度为O(N),排序的时间复杂度为O(NlogN),最大项为NlogN,因此堆排序的时间复杂度为O(N*logN)
关于其他排序,后续会依次介绍。