1.二叉树的分层遍历

OJ链接

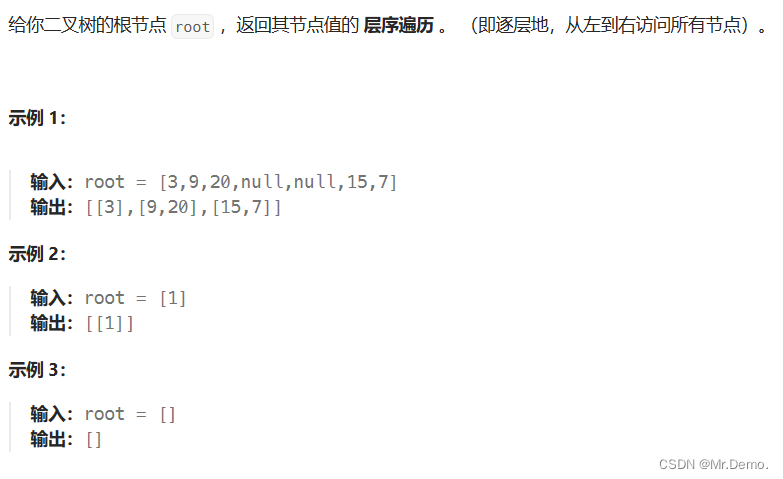
上面这道题是分层式的层序遍历,每一层有哪些结点都很明确,我们先想一想普通的层序遍历怎么做

/*** 层序遍历* @param root*/public void levelOrder1(Node root){Queue<Node> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){Node cur = queue.poll();System.out.println(cur.value);if (cur.left != null){queue.offer(cur.left);}if (cur.right != null){queue.offer(cur.right);}}}

这里我们通过申请队列的方式来实现层序遍历.按照从左到右的方式依次把结点依次存入队列中.

整体思路:

1. 首先把根节点放入队列中,之后让根结点出队列.
2. 把根结点的左结点和右结点放入队列中.
3. 第二层放完之后,再把根结点的左结点出队列,把它的左右结点再放入队列中.再把根结点的右结点出队列,把它的左右结点再放入队列中.
4. 以此类推,这样便可以做到从左到右,从上到下.

下面我们来实现分层操作:

/*** 层序遍历(分层)* @param root* @return*/public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> lists = new ArrayList<>();Queue<Node> queue = new LinkedList<>();if (root == null){//root为空直接返回空列表return lists;}queue.offer(root);//把根节点放进去while (!queue.isEmpty()){//队列不为空继续给lists中添加元素int size = queue.size();//获取队列大小,就是该层元素的大小List<Integer> list = new ArrayList<>();//每一层都有一个Listwhile (size != 0){//当size--为0的时候,证明这一层添加完成Node cur = queue.poll();list.add(cur.value);//忽略警告,下面的两个条件会把cur限制住if (cur.left != null){//左子树不为空,把根的左结点放进来queue.offer(cur.left);}if (cur.right != null){queue.offer(cur.right);//右子树不为空,把根的右结点放进来}size--;}lists.add(list);//每一层遍历完都添加到lists中}return lists;}

技巧性:

这里使用了size这个巧妙的变量,用来记录当前队列的大小.我们每一层都会申请一个list,把当前层数中的结点全部放入该list中,当队列的size–为0 ,说明该层的结点遍历完成,把该层的list放入总的lists中.

子问题:判断一棵树是否是完全二叉树

/*** 判断一棵树是否是完全二叉树* @param root* @return*/public boolean isCompeteTree(Node root){Queue<Node> queue = new LinkedList<>();//申请队列queue.offer(root);//把根节点放入Node cur = queue.poll();//弹出根节点赋给curwhile (cur != null){queue.offer(cur.left);queue.offer(cur.right);cur = queue.poll();//这里需要注意的是,根结点的左右子树如果为null也要放入}while(!queue.isEmpty()){Node cur1 = queue.poll();if (cur1 != null){return false;//让元素出队列,如果出的过程中遇到不是空的情况,说明不是完全二叉树}}return true;}

整体思路:
我们下面只介绍与上面问题不同的地方

1. 这道题和上面的问题有所不同的一个点就是,即使遍历到最后,cur的左右仍然为空,也要放入队列中.
2. 在遍历完成之后出队列的时候,如果在出到不等于null的元素,即在层序遍历完成之后,队列中仍然存在元素,此时就不是完全二叉树,否者为完全二叉树.

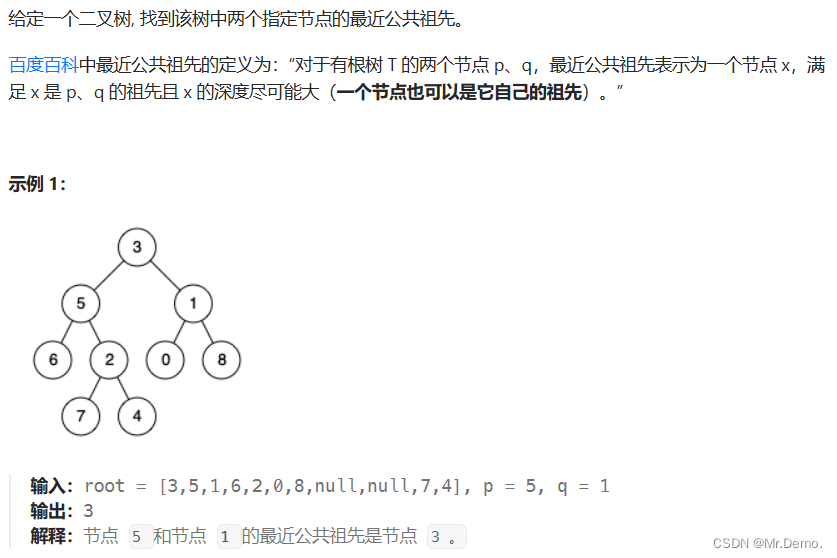
2. 最近公共祖先

OJ链接

/*** 寻找公共祖先,分为root是p,q中的一个,在root同侧,在root异侧* @param root* @param p* @param q* @return*/public Node lowestCommonAncestor(Node root, Node p, Node q) {if (root == null){return null;//如果是空树返回null}if (root == p || root == q){return root;//如果p或者q中有一个是根结点,那么根结点就是公共祖先}Node leftnode = lowestCommonAncestor(root.left,p,q);//向左子树递归Node rightnode = lowestCommonAncestor(root.right,p,q);//向右子树递归if (leftnode != null && rightnode != null){return root;//如果左子树和右子树返回的都不是null,说明p,q在root两侧,root是公共祖先} else if (leftnode == null) {return rightnode;//如果左子树返回null,说明p,q同在root右侧,返回右侧先找到的结点}else {return leftnode;//同理}}

这道题分为这几种情况:

1. p,q其中有一个是根结点,直接返回root.
2. p,q在根结点的异侧,则在返回的时候,根结点左子树和右子树返回的都不是空,这种情况返回的就是root.
3. p,q在根结点的同侧,根结点左子树或者右子树有其中一个返回空,那么它们的子树中又有可能是上面的1或者2中的情况,返回子树得到的返回值即可.

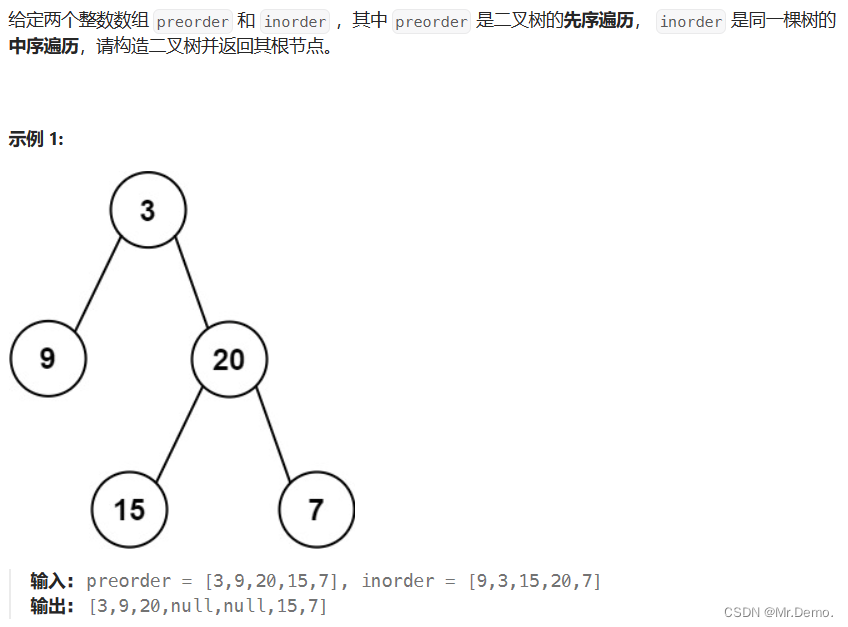
3. 中序前序遍历构造二叉树

OJ链接

/*** 中序前序遍历构造二叉树* @param preorder 前序遍历* @param inorder 中序遍历* @return*/public int preindex = 0;//注意遍历前序数组的时候,要设置为成员变量public Node buildTree(int[] preorder, int[] inorder) {return buildTreeChild(preorder,inorder,0,inorder.length-1);}private Node buildTreeChild (int[] preorder, int[] inorder, int ibegin ,int iend){if (ibegin > iend){return null;//遍历中序数组,遍历到头大于尾的时候,返回null}int inorderindex = findIndex(inorder,preorder[preindex],ibegin,iend);//在中序数组中寻找前序遍历到的字符串//找到的即为树的根结点preindex ++;//向后遍历前序数组Node node = new Node(inorder[inorderindex]);//创建结点Node leftnode = buildTreeChild(preorder,inorder,ibegin,inorderindex-1);node.left = leftnode;//向中序数组的左遍历,构建左子树Node rightnode = buildTreeChild(preorder,inorder,inorderindex+1,iend);node.right = rightnode;//向中序数组的右遍历,构建右子树return node;}private int findIndex (int[] inorder, int order,int ibegin, int iend){for (int i = ibegin; i <= iend; i++) {if (inorder[i] == order){return i;}}return -1;}

整体思路:

1. 由于前序遍历可以决定根节点,所以我们要拿着前序遍历数组的元素在中序遍历数组的的元素中寻找对应元素,即根结点,并创建根结点.并找到中序遍历数组中对应的下标位置.(inorderindex)
2. 之后创建左子树,向下递归,在0~inorderindex-1的范围之中创建左子树.
3. 之后创建右子树,向下递归,在inorderindex+1~inorder.length-1的范围之中创建右子树.

注意:
遍历前序数组的preindex应该设置为成员变量,否者在每次递归的时候preindex不会向下走,又会返回原来的值.

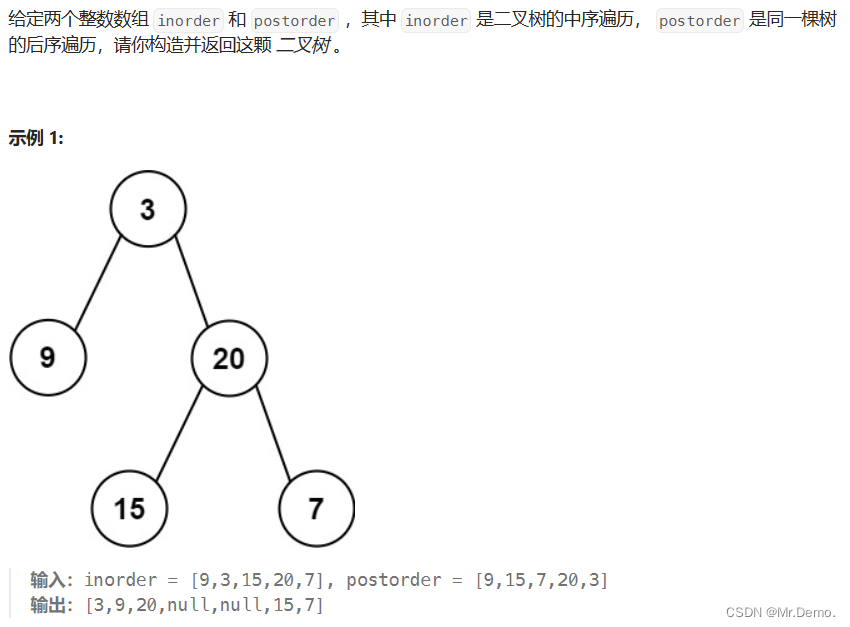
4. 后序遍历和中序遍历构建二叉树

OJ链接

/*** 后序遍历和中序遍历构建二叉树* @param inorder* @param postorder* @return*/public int postindex = 0;public Node buildTree2(int[] inorder, int[] postorder) {postindex = postorder.length-1;return buildTreeChild2(inorder,postorder,0,inorder.length-1);}private Node buildTreeChild2(int[] inoder, int[] postorder,int ibegin,int iend){if (ibegin > iend){return null;}int inorderindex = findIndex2(inoder,postorder[postindex],ibegin,iend);Node node = new Node(inoder[inorderindex]);postindex--;Node rightnode = buildTreeChild2(inoder,postorder,inorderindex+1,iend);node.right = rightnode;Node leftnode = buildTreeChild2(inoder,postorder,ibegin,inorderindex-1);node.left = leftnode;//由于后序遍历数组的顺序为左右根,所以在从后向前遍历的时候,遍历完根之后是右//所以要先构建右子树,再构建左子树return node;}private int findIndex2(int[] inorder,int order,int ibegin,int iend){for (int i = ibegin; i <= iend; i++) {if (order == inorder[i]){return i;}}return -1;}

注意:

1. 与前序遍历不同的是,这里遍历后序数组的变量为postindex,大小为postorder.length-1,在途中让postindex- -.
2. 子树先构建右子树,再构建左子树,因为:由于后序遍历数组的顺序为左右根,所以在从后向前遍历的时候,遍历完根之后是右,所以要先构建右子树,再构建左子树.

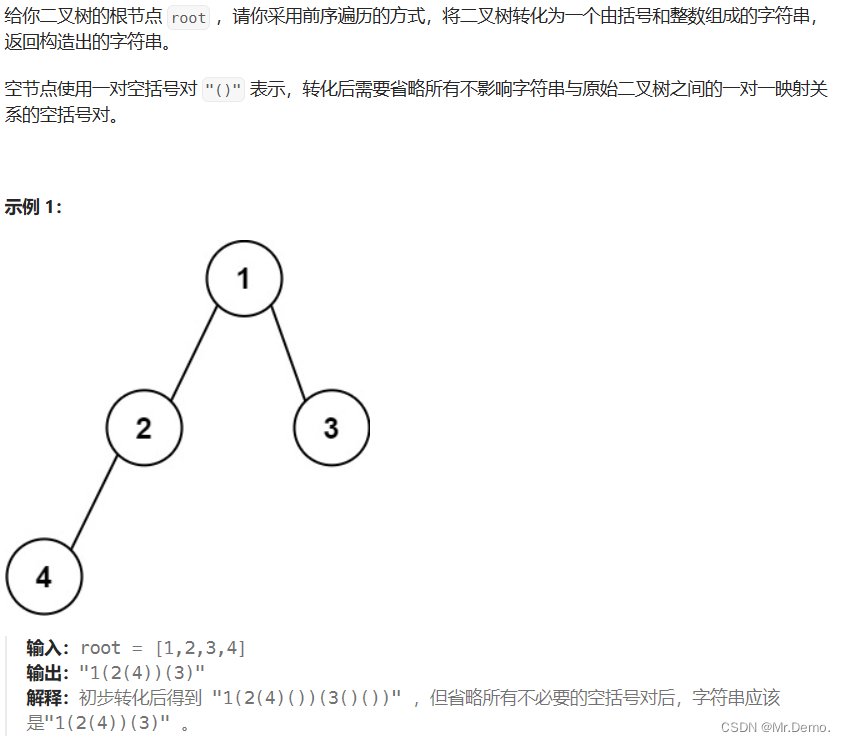
5. 根据二叉树创建字符串(采用前序遍历)

OJ链接

/*** 根据二叉树创建字符串,采用前序遍历* @param root* @return*/StringBuilder stringBuilder = new StringBuilder();//创建stringbuilderpublic String tree2str(Node root) {if (root == null){return null;//空树返回null}stringBuilder.append(root.value);//添加根结点的值if (root.left != null){stringBuilder.append("(");tree2str(root.left);//添加左结点stringBuilder.append(")");}else {if (root.right != null){stringBuilder.append("()");//如果左结点为空,看右结点是否为空,如果不为空,添加()}}if (root.right != null){//添加右结点stringBuilder.append("(");tree2str(root.right);stringBuilder.append(")");}return stringBuilder.toString();}

整体思路:

1. 创建StringBuilder对象.
2. 先把根结点放入,之后向左子树遍历.
3. 如果左结点不为空,键入括号,并键入左结点的值.
4. 如果左结点为空,又分为两种情况:右结点为空,直接什么都不做,右结点不为空,键入空的括号.
5. 向右子树遍历.
6. 构建好StringBilder对象之后,使用toString方法转为String.

6. 二叉树的非递归前序遍历

OJ链接

/*** 二叉树的非递归前序遍历 ->借助栈* @param root* @return*/public List<Integer> preorderTraversal(Node root) {List<Integer> list = new ArrayList<>();//创建顺序表if (root == null){return list;//如果为空树,返回空顺序表}Stack<Node> stack = new Stack<>();//创建栈,使用栈代替递归Node cur = root;//cur指向根while (cur != null || !stack.isEmpty()) {while (cur != null) {//cur遍历到空stack.push(cur);//把根结点放入栈中,用入栈的方式代替递归中递的过程list.add(cur.value);//并放入顺序表,完成了前序遍历的第一步,根cur = cur.left;//向左遍历,完成了前序遍历的第二部,左//循环回去又是下一个根,有到了前序遍历的第一步}Node top = stack.pop();//开始返回,用出栈的方式代替递归的归的过程cur = top.right;//cur遍历到右结点,循环回去完成了前序遍历的第三部,右}return list;}

整体思路:

1. 该题需要借助栈来代替递归的过程.
2. 先使得cur指向root.
3. 把cur放入栈中,并放入list中,之后cur向左结点走,依次都把向左走的结点放入栈中.
4. 在出栈的时候,top得到出栈元素,拿着出栈元素找到top结点的右结点,之后依次循环3,4两步.

注意:

1. 在top拿到出栈元素之后,如果没有外层循环,该结点右结点就无法执行思路中的第三步.
2. 出栈的时候,栈有可能为空,所以要添加!stack.isEmpty().

7. 二叉树的非递归中序遍历

/*** 二叉树的非递归中序遍历 ->借助栈* @param root* @return*/public List<Integer> inorderTraversal(Node root) {List<Integer> list = new ArrayList<>();//创建顺序表if (root == null){return list;//如果为空树,返回空顺序表}Stack<Node> stack = new Stack<>();//创建栈,使用栈代替递归Node cur = root;//cur指向根while (cur != null || !stack.isEmpty()) {while (cur != null) {//cur遍历到空stack.push(cur);//把根结点放入栈中,用入栈的方式代替递归中递的过程cur = cur.left;//向左遍历//循环回去,让左结点入栈}Node top = stack.pop();//开始返回,用出栈的方式代替递归的归的过程list.add(top.value);//为顺序表添加结点cur = top.right;//cur遍历到右结点//循环回去,可能遍历到最后,top的右节点是空,但是栈不为空,走下来就可以把根节点放入list中}return list;}

与前序的不同点:

1. 在左结点入栈的时候,不入list
2. 在最后出栈的时候先把左结点放入list中,最后cur的右为null,但是栈不为空,所以可以进入下一层循环,就可以得到原来cur上一层的根节点.

8. 二叉树的非递归后序遍历

OJ链接

public List<Integer> postorderTraversal(Node root) {List<Integer> list = new ArrayList<>();if (root == null) {return list;}Stack<Node> stack = new Stack<>();Node cur = root;Node prev = null;while (cur != null || !stack.isEmpty()) {while (cur != null) {stack.push(cur);cur = cur.left;}Node top = stack.peek();if (top.right == null || top.right == prev) {stack.pop();list.add(top.value);prev = top;} else {cur = top.right;}}return list;}

注意:
在走到最后的时候,会出现死循环,所以我们要使用prev来记录最近存入list的结点,以避免死循环