摘要

本文主要讨论PINN。本文简要介绍了监督学习。其次本文展示了题为Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations的论文主要内容。该论文提出了一个深度学习框架，使数学模型和数据能够协同结合。该文以此为基础引出了一种有效机制，用于在较小数据规模下规范化深度神经网络的训练。该方法能够在不完整的模型以及数据中推测出较为合理的结果。本文主要集中在该文第三节——偏微分方程的数据驱动解。最后，本文基于pytorch实现了PINN并使用该模型预测Burgers方程。

Abstract

This article focuses on the PINN. This article provides a brief introduction to supervised learning. Secondly, this paper presents the main content of the paper entitled Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. The paper proposes a deep learning framework that enables mathematical models and data to be synergistically combined. Based on this, the paper proposes an effective mechanism for the training of normalized deep neural networks at a small data scale. This method can infer reasonable results from incomplete models and data. This article focuses on the third section of the paper, data-driven solutions to partial differential equations. Finally, this article implements PINN based on pytorch and uses the model to predict the Burgers equation.

一、监督学习

监督学习就是学习输入、输出，也就是从输入到输出的映射。监督学习的数据集就是有标签的，这个数据集由“正确答案”组成，也就是是人们给机器一大堆标记好的数据，比如一大堆照片，标记住那些是猫的照片，那些是狗的照片，然后让机器自己学习归纳出算法或模型，然后所使用该算法或模型判断出其他照片是否是猫或狗。

监督学习问题的类型分为两种：回归问题和分类问题。

对输入变量和输出变量均为连续变量的预测问题称为 回归问题。
输出变量为有限个离散变量的预测问题称为 分类问题。
回归问题
回归问题，我们试着推测出一个连续值的结果，一般应用于预测等任务。回归的目的是为了找到最优拟合的曲线，这个曲线可以最好的接近数据集中的各个点。回归是对真实值的一种逼近预测，值不确定，当预测值与真实值相近时，误差较小时，认为这是一个好的回归。

线性回归
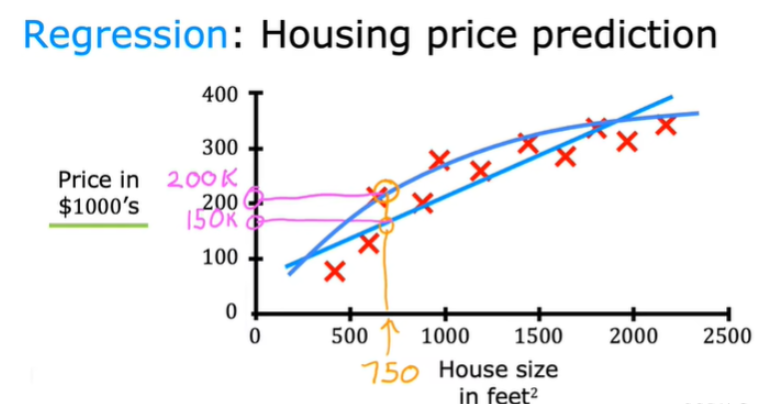
下图收集一些房价的数据：横轴表示房子的面积，单位是平方英尺，纵轴表示房价，单位是千美元。那基于这组数据，假如你有一个朋友，他有一套750平方英尺房子，现在他希望把房子卖掉，他想知道这房子能卖多少钱。机器学习算法可以在这组数据拟合一条直线，根据这条线我们可以推测出，这套房子可能卖$150,00（也可能拟合的是二次方程的曲线效果更好，因此算法不是唯一的）。在房价的例子中，我们给了一系列房子的数据，我们给定数据集中每个样本的正确价格，即它们实际的售价，然后运用学习算法，算出更多的正确答案。

线性回归数学原理

线性回归模型

线性回归模型是用一条曲线拟合一个或多个自变量x与因变量y之间的关系。若曲线是一条直线，则为一元线性回归；若是超平面，则是多元线性回归。不管是一维还是多维，线性回归的预测函数的一般表达式为：
$$f(x_i)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_m{x}_m\text{\hspace{1em}(1)}$$
令$x_0=1$带入上式有
$$f(x_i)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_m{x}_m=\sum _{i=1}^m{\theta }_i{x}_i\text{\hspace{1em}(2)}$$
转换为向量形式有
$$f(x)={\theta }^{T}x+b\text{\hspace{1em}(3)}$$

二、文献阅读

该文篇幅较大，本文主要介绍偏微分方程的数据驱动解，另一部分数据驱动偏微分方程的发现将在下周介绍

1. 题目

题目：Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations

作者：M. Raissi, P. Perdikaris , G.E. Karniadakis

链接：https://www.sciencedirect.com/science/article/pii/S0021999118307125

发布：Journal of Computational Physics Volume 378, 1 February 2019, Pages 686-707

2. abstract

该文引入了基于物理的神经网络。这项工作在解决两类主要问题的背景下展示了进展：数据驱动的解决方案和数据驱动的偏微分方程发现。根据可用数据的性质和排列，该文设计了两种不同类型的算法，即连续时间模型和离散时间模型。该框架的有效性通过流体、量子力学、反应扩散系统和非线性浅水波传播中的一系列经典问题得到了证明。

We introduce physics-informed neural networks. This work presents the developments in the context of solving two main classes of problems: data-driven solution and data-driven discovery of partial differential equations. Depending on the nature and arrangement of the available data, this article devise two distinct types of algorithms, namely continuous time and discrete time models. The effectiveness of the proposed framework is demonstrated through a collection of classical problems in fluids, quantum mechanics, reaction–diffusion systems, and the propagation of nonlinear shallow-water waves.

3. 偏微分方程的数据驱动解

一般形式的偏微分方程的数据驱动解的问题
$$u_t+\mathcal{N}[u;\lambda ]=0,x\in \Omega ,t\in [0,T]\text{\hspace{1em}(2)}$$
该文提出了两种不同类型的算法，即连续时间模型和离散时间模型，以及通过不同基准问题的视角突出它们的属性和性能。

3.1连续时间模型

根据2式，将f定义为如下形式
$$f:=u_t+\mathcal{N}[u]\text{\hspace{1em}(3)}$$
通过深度神经网络逼近 $u(t,x)$。神经网络 $u(t,x)$ 和 $f(t,x)$ 之间的共享参数可以通过最小化均方误差损失来学习
$$\begin{gathered} MSE=MS{E}_u+MS{E}_f \\ whereMS{E}_u=\frac{1}{N_u}\sum _{i=1}^{N_u}|u(t_u^i,x_u^i)-u^i{|}^2 \\ MS{E}_f=\frac{1}{N_f}\sum _{i=1}^{N_f}|f(t_f^i,x_f^i){|}^2\text{\hspace{1em}(4)} \end{gathered}$$
损失 $MS{E}_u$ 对应于初始数据和边界数据，而 $MS{E}_f$ 在一组有限的配置点处强制执行方程 (2) 所强加的结构。

在这里，使用深度学习社区所采用的完全相同的自动微分技术，通过对输入坐标（即空间和时间）求导来为神经网络提供物理信息，其中物理现象由偏微分方程描述。凭经验观察到，这种结构化方法引入了正则化机制，便于使用相对简单的前馈神经网络架构并用少量数据对其进行训练

在与偏微分方程的数据驱动解有关的所有情况下，训练数据 $N_u$ 的总数相对较小，故选择使用 L-BFGS 来优化所有损失函数。对于较大的数据集，可以使用随机梯度下降及其现代变体轻松采用计算效率更高的小批量设置。

example(Schrodinger equation)：

为了评估方法的准确性，使用传统光谱方法模拟方程（5）来创建高分辨率数据集。具体来说，从初始状态 $h(0,x)=2sech(x)$ 开始，假设周期性边界条件 $h(t,-5)=h(t,5)$ 且 $h_x(t,-5)=h_x(t，5)$，使用 Chebfun 包将方程（5）积分到最终时间 $t=\pi /2$，该包具有 256 个模式的谱傅立叶离散化和具有时间的四阶显式龙格-库塔时间积分器步骤$t=\pi /2\cdot 10^{-6}$。在数据驱动设置下，观察到的只是在时间 $t=0$ 时潜在函数 $h(t,x)$ 的测量值 { x 0 i , h 0 i } i = 1 N 0 \{x^i_0, h^i_0\}^{N_0}_{i=1} {x0i​,h0i​}i=1N0​​。特别是，训练集总共包含从完整高分辨率数据集中随机解析$h(0,x)$ 上的 $N_0=50$ 个数据点，以及用于强制周期性边界的 $N_b=50$ 个随机采样搭配点 { t b i } i = 1 N b \{t^i_b\}^{N_b}_{i=1} {tbi​}i=1Nb​​。此外，假设 $N_f=20,000$ 个随机采样的配置点，用于在解域内强制执行方程 (5)。所有随机采样点位置都是使用空间填充拉丁超立方采样策略生成的。

使用每层 100 个神经元的 5 层深度神经网络和双曲正切激活函数来联合表示潜在函数 $h(t,x)=[u(t,x)v(t,x)]$。

该文提出了未来的研究方向，为了给神经网络足够的逼近能力以适应 $u(t,x)$​ 的预期复杂性，可以采用贝叶斯方法并监测预测后验分布的方差。

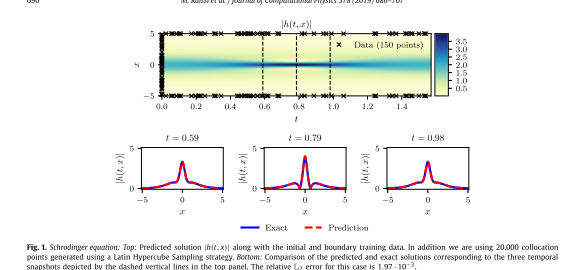
下图总结了实验结果。具体来说，下图的顶部面板显示了预测的时空解 $|h(t,x)|=\sqrt{u^2(t,x)+v^2(t,x)}$ ，以及初始和边界训练数据的位置。由此产生的预测误差根据该问题的测试数据进行验证，并在相对 L2 范数中测量为 1.97 · 10−3。下图的底部面板显示了对预测解的更详细评估。对不同时刻 t = 0.59、0.79、0.98 时的精确解和预测解进行了比较。

仅使用少量初始数据，基于物理的神经网络就可以准确捕获薛定谔方程复杂的非线性行为。

3.2离散时间模型

Example (Allen–Cahn equation)：

训练数据集由 Nn = 200 个初始数据点组成，这些数据点是从时间 t = 0.1 时的精确解中随机子采样的，目标是使用大小为 的单个时间步长来预测时间 t = 0.9 时的解t = 0.8。为此，采用离散时间物理信息神经网络，具有 4 个隐藏层，每层 200 个神经元，而输出层预测q = 100阶的 Runge-Kutta 的$ u^{n+ci} (x)\ i = 1、…、q$ 的 101 个感兴趣的量，以及最终时间 $u^{n+1}(x)$ 的解。该方案的理论误差估计预测时间误差累积为 $O(\Delta t^{2q})$ ，本例中误差较小。值得注意的是，从 t = 0.1 处的平滑初始数据开始，可以在单个时间步中预测 t = 0.9 处的近不连续解，相对 L2 误差为 $6.99\cdot 10^{-3}$，如下图所示。该误差为完全归因于神经网络近似 u(t, x) 的能力，以及误差平方和损失允许对训练数据进行插值的程度。

在离散时间模型下拟合该方程，以最小化误差平方和作为损失函数

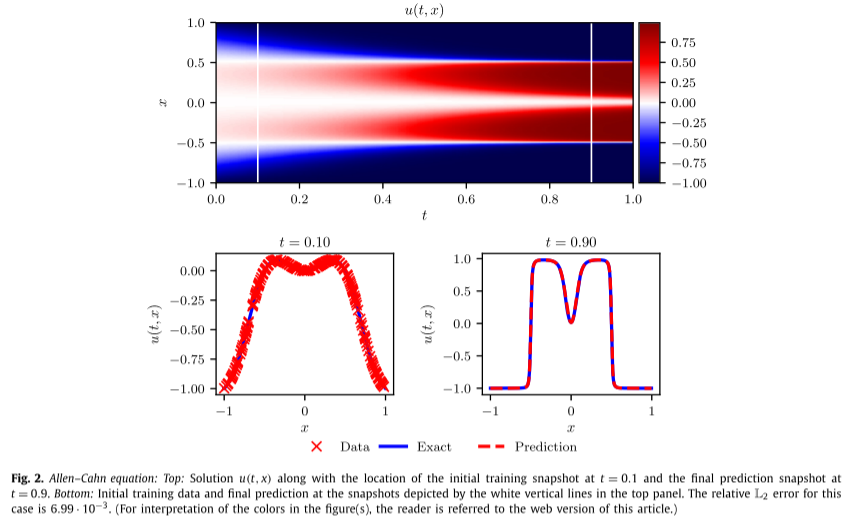
如上图所示。该网络的误差主要来源于网络拟合能力，而非其是否契合物理规则，以及误差平方和损失允许对训练数据进行插值的程度。

控制离散时间算法性能的关键参数是龙格-库塔阶段总数 q 和时间步长 t。在此框架下，网络同时具有了高效性与稳定性，因此使其成为解决刚性问题的理想选择。

4. 文献解读

4.1 Introduction

在小数据体系中，绝大多数最先进的机器学习技术缺乏鲁棒性，无法提供任何收敛保证。存在大量的知识目前尚未在现代机器学习实践中得到利用。这些先验信息可以充当正则化代理，将可接受的解决方案的空间限制在可管理的大小。最近的研究已经首次展示了利用结构化先验信息来构建数据高效且基于物理的学习机器的希望。尽管高斯过程在编码先验信息方面具有灵活性和数学优雅性，但非线性问题的处理引入了重要的限制。高斯过程回归的贝叶斯性质需要某些先验假设，这些假设可能会限制模型的表示能力并引起鲁棒性/脆弱性问题，特别是对于非线性问题

4.2 创新点

1. 提出了一个深度学习框架，使数学模型和数据能够协同结合。
2. 介绍了一种有效的机制，用于在小数据制度下规范化深度神经网络的训练。
3. 所提出的方法能够从不完整的模型和不完整的数据中进行科学的预测和发现。

在这项工作中，采用了不同的方法，采用深度神经网络并利用其作为通用函数逼近器的功能。在这种情况下，可以直接解决非线性问题，而无需承诺任何先前的假设、线性化或局部时间步进。这种神经网络必须遵守源自控制观测数据的物理定律的任何对称性、不变性或守恒原理。这种简单而强大的结构使得能够解决计算科学中的各种问题，并引入了一种潜在的变革性技术，从而促进开发新的数据高效和物理信息学习机器、偏微分方程的新型数值求解器。

这项工作的总体目标是为建模和计算的新范式奠定基础，通过数学物理学的长期发展丰富深度学习。在整个工作中，我们一直使用相对简单的深度前馈神经网络架构，具有双曲正切激活函数，并且没有额外的正则化。

在这项工作中，考虑一般形式的参数化和非线性偏微分方程
$$u_t+\mathcal{N}[u;\lambda ]=0,x\in \Omega ,t\in [0,T]$$
其中 $u(t,x)$ 表示潜在（隐藏）解，$\mathcal{N}[\cdot ；\lambda ]$ 是由 λ 参数化的非线性算子，并且是 ${\mathbb{R}}^D$​ 的子集。该设置涵盖了数学物理中的广泛问题，包括守恒定律、扩散过程、平流扩散反应系统和动力学方程。

一维 Burgers 方程
$$N[u;\lambda ]={\lambda }_{1}u{u}_x-{\lambda }_2{u}_{xx},\lambda =({\lambda }_1,{\lambda }_2)$$
作为一个激励性的例子，对应于 。这里，下标表示时间或空间上的偏微分。

考虑到系统的噪声测量，该文主要对两个不同问题的解决方案进行了一定的研究。

• 第一个问题是偏微分方程的推理、滤波和平滑或数据驱动解决方案，其中指出：给定固定模型参数 λ，关于未知隐藏状态 u(t, x) 可以说些什么系统？
• 第二个问题是学习、系统识别或数据驱动的偏微分方程发现，其中指出：最能描述观测数据的参数 λ 是什么？

三、实验内容

1.实验要求

本实验旨在使用pytorch实现PINN，并使用该网络拟合Burgers方程

实验理论依据：参见https://maziarraissi.github.io/PINNs/

代码来源于Github https://github.com/jayroxis/PINNs

考虑Burgers方程，如下图所示，初始时刻u符合sin分布，随着时间推移在x=0处发生间断.
这是一个经典问题，可使用pytorch通过PINN实现对Burgers方程的求解。

• network.py文件用于定义神经网络的结构
• train.py文件用于训练神经网络
• evaluate.py文件用于测试训练好的模型绘制结果图

2.实验结果

训练损失

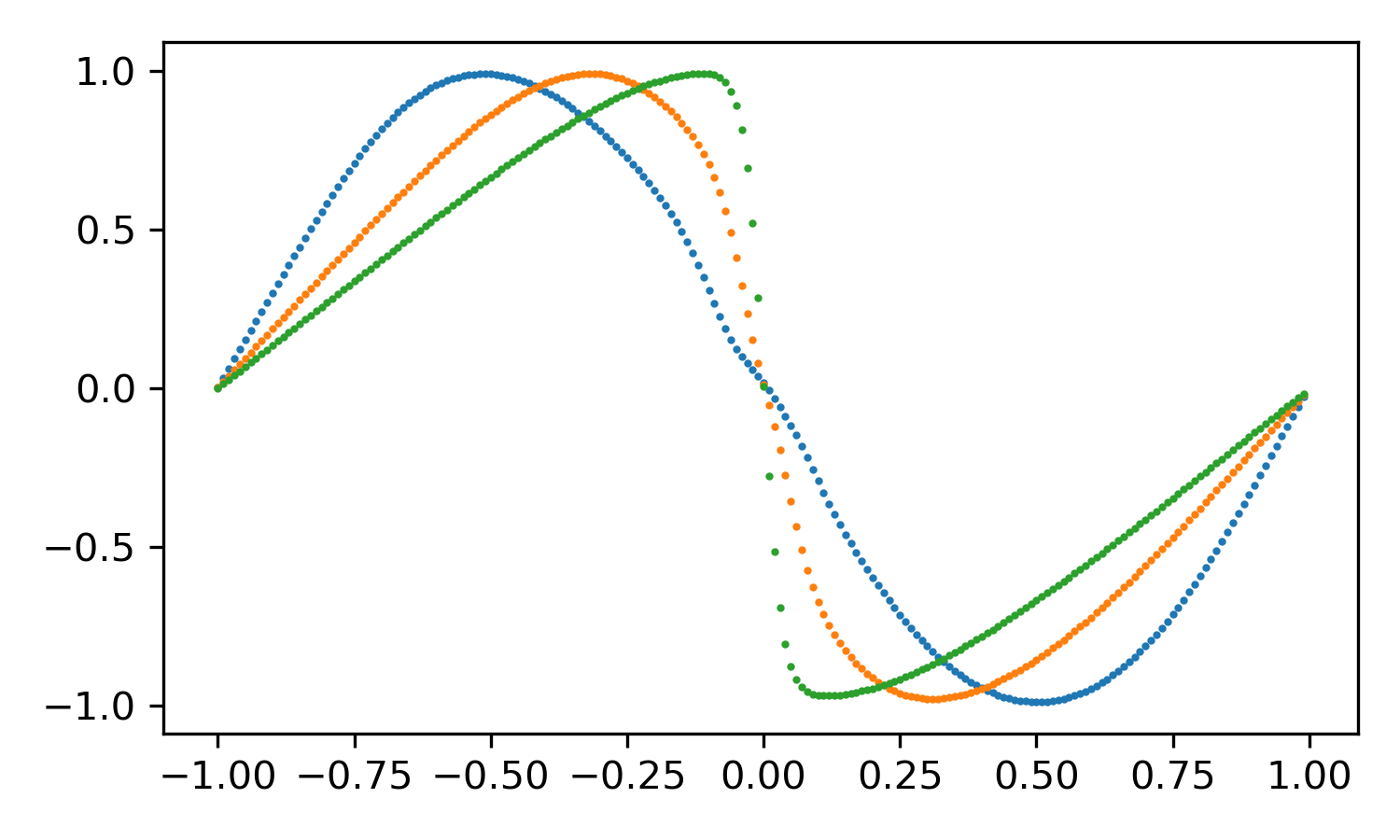
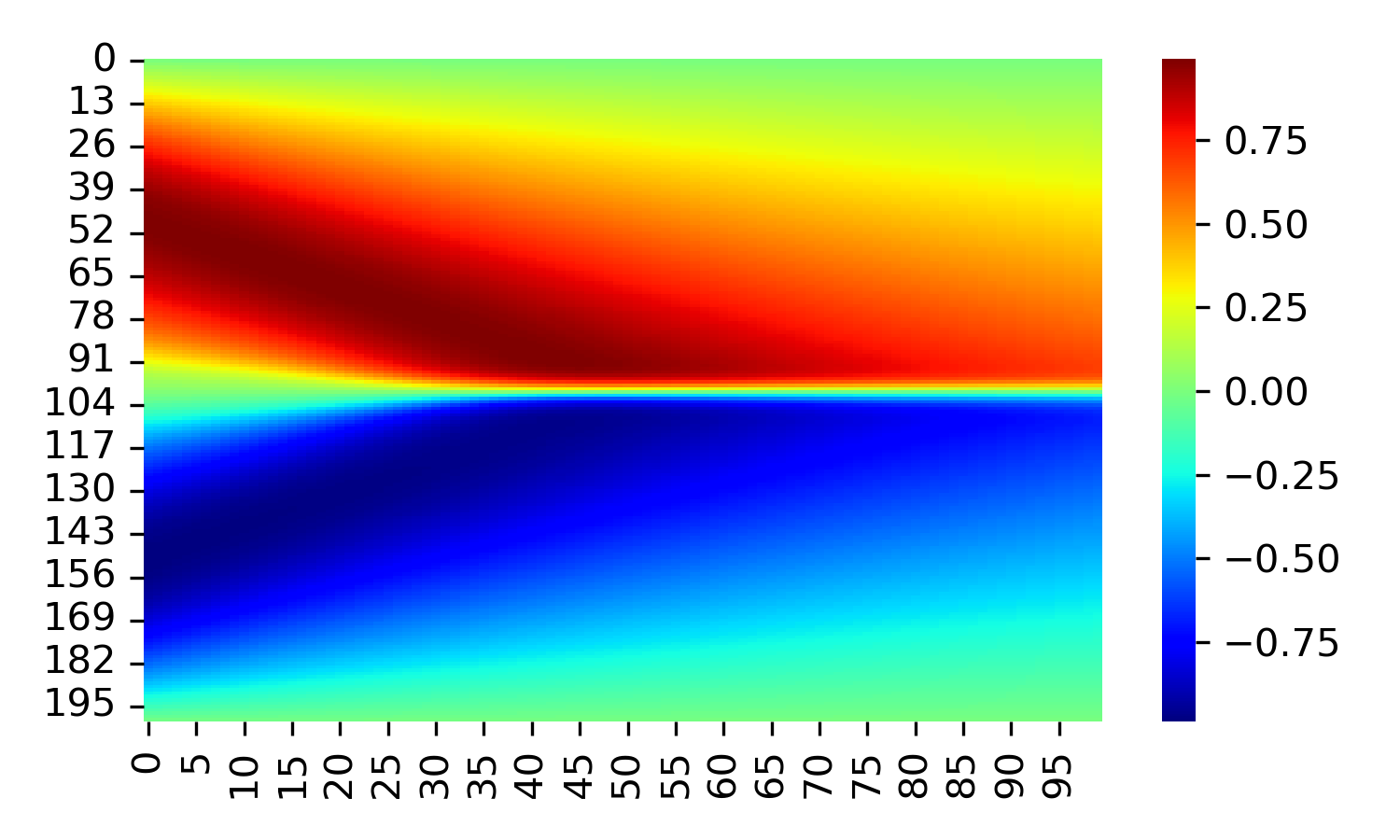
训练完成模型后使用matplotlib绘制u场图形如下

3.实验代码

3.1network.py

OrderedDict：顾名思义，可以记录插入字典的顺序，但初始化值同序

该部分构建网络主要使用了Linear，即线性层；激活函数torch.nn.Tanh

import torch
import torch.nn as nn
from collections import OrderedDict# 定义神经网络的架构
class Network(nn.Module):# 构造函数def __init__(self,input_size, # 输入层神经元数hidden_size, # 隐藏层神经元数output_size, # 输出层神经元数depth, # 隐藏层数act=torch.nn.Tanh, # 输入层和隐藏层的激活函数):super(Network, self).__init__()#调用父类的构造函数# 输入层layers = [('input', torch.nn.Linear(input_size, hidden_size))]layers.append(('input_activation', act()))# 隐藏层for i in range(depth):layers.append(('hidden_%d' % i, torch.nn.Linear(hidden_size, hidden_size)))layers.append(('activation_%d' % i, act()))# 输出层layers.append(('output', torch.nn.Linear(hidden_size, output_size)))#将这些层组装为神经网络self.layers = torch.nn.Sequential(OrderedDict(layers))# 前向计算方法def forward(self, x):return self.layers(x)

3.2 train.py

本部分除了构建训练过程外，还需要提供模型参数，从而调用上文代码构建网络，构建完成后进行训练。

import math
import torch
import numpy as np
from network import Network# 定义一个类，用于实现PINN(Physics-informed Neural Networks)
class PINN:# 构造函数def __init__(self):# 选择使用GPU还是CPUdevice = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")# 定义神经网络self.model = Network(input_size=2,  # 输入层神经元数hidden_size=16,  # 隐藏层神经元数output_size=1,  # 输出层神经元数depth=8,  # 隐藏层数act=torch.nn.Tanh  # 输入层和隐藏层的激活函数).to(device)  # 将这个神经网络存储在GPU上（若GPU可用）self.h = 0.1  # 设置空间步长self.k = 0.1  # 设置时间步长x = torch.arange(-1, 1 + self.h, self.h)  # 在[-1,1]区间上均匀取值，记为xt = torch.arange(0, 1 + self.k, self.k)  # 在[0,1]区间上均匀取值，记为t# 将x和t组合，形成时间空间网格，记录在张量X_inside中self.X_inside = torch.stack(torch.meshgrid(x, t)).reshape(2, -1).T# 边界处的时空坐标bc1 = torch.stack(torch.meshgrid(x[0], t)).reshape(2, -1).T  # x=-1边界bc2 = torch.stack(torch.meshgrid(x[-1], t)).reshape(2, -1).T  # x=+1边界ic = torch.stack(torch.meshgrid(x, t[0])).reshape(2, -1).T  # t=0边界self.X_boundary = torch.cat([bc1, bc2, ic])  # 将所有边界处的时空坐标点整合为一个张量# 边界处的u值u_bc1 = torch.zeros(len(bc1))  # x=-1边界处采用第一类边界条件u=0u_bc2 = torch.zeros(len(bc2))  # x=+1边界处采用第一类边界条件u=0u_ic = -torch.sin(math.pi * ic[:, 0])  # t=0边界处采用第一类边界条件u=-sin(pi*x)self.U_boundary = torch.cat([u_bc1, u_bc2, u_ic])  # 将所有边界处的u值整合为一个张量self.U_boundary = self.U_boundary.unsqueeze(1)# 将数据拷贝到GPUself.X_inside = self.X_inside.to(device)self.X_boundary = self.X_boundary.to(device)self.U_boundary = self.U_boundary.to(device)self.X_inside.requires_grad = True  # 设置：需要计算对X的梯度# 设置准则函数为MSE，方便后续计算MSEself.criterion = torch.nn.MSELoss()# 定义迭代序号，记录调用了多少次lossself.iter = 1# 设置lbfgs优化器self.lbfgs = torch.optim.LBFGS(self.model.parameters(),lr=1.0,max_iter=50000,max_eval=50000,history_size=50,tolerance_grad=1e-7,tolerance_change=1.0 * np.finfo(float).eps,line_search_fn="strong_wolfe",)# 设置adam优化器self.adam = torch.optim.Adam(self.model.parameters())# 损失函数def loss_func(self):# 将导数清零self.adam.zero_grad()self.lbfgs.zero_grad()# 第一部分loss: 边界条件不吻合产生的lossU_pred_boundary = self.model(self.X_boundary)  # 使用当前模型计算u在边界处的预测值loss_boundary = self.criterion(U_pred_boundary, self.U_boundary)  # 计算边界处的MSE# 第二部分loss:内点非物理产生的lossU_inside = self.model(self.X_inside)  # 使用当前模型计算内点处的预测值# 使用自动求导方法得到U对X的导数du_dX = torch.autograd.grad(inputs=self.X_inside,outputs=U_inside,grad_outputs=torch.ones_like(U_inside),retain_graph=True,create_graph=True)[0]du_dx = du_dX[:, 0]  # 提取对第x的导数du_dt = du_dX[:, 1]  # 提取对第t的导数# 使用自动求导方法得到U对X的二阶导数du_dxx = torch.autograd.grad(inputs=self.X_inside,outputs=du_dX,grad_outputs=torch.ones_like(du_dX),retain_graph=True,create_graph=True)[0][:, 0]loss_equation = self.criterion(du_dt + U_inside.squeeze() * du_dx, 0.01 / math.pi * du_dxx)  # 计算物理方程的MSE# 最终的loss由两项组成loss = loss_equation + loss_boundary# loss反向传播，用于给优化器提供梯度信息loss.backward()# 每计算100次loss在控制台上输出消息if self.iter % 100 == 0:print(self.iter, loss.item())self.iter = self.iter + 1return loss# 训练def train(self):self.model.train()  # 设置模型为训练模式# 首先运行5000步Adam优化器print("采用Adam优化器")for i in range(5000):self.adam.step(self.loss_func)# 然后运行lbfgs优化器print("采用L-BFGS优化器")self.lbfgs.step(self.loss_func)# 实例化PINN
pinn = PINN()# 开始训练
pinn.train()# 将模型保存到文件
torch.save(pinn.model, 'model.pth')

3.3 evaluate.py

使用训练完成的模型评估预测函数，并生成图像作为可视化结果。

import torch
import seaborn as sns
import matplotlib.pyplot as plt# 选择GPU或CPU
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")# 从文件加载已经训练完成的模型
model_loaded = torch.load('model.pth', map_location=device)
model_loaded.eval()  # 设置模型为evaluation状态# 生成时空网格
h = 0.01
k = 0.01
x = torch.arange(-1, 1, h)
t = torch.arange(0, 1, k)
X = torch.stack(torch.meshgrid(x, t)).reshape(2, -1).T
X = X.to(device)# 计算该时空网格对应的预测值
with torch.no_grad():U_pred = model_loaded(X).reshape(len(x), len(t)).cpu().numpy()# 绘制计算结果
plt.figure(figsize=(5, 3), dpi=300)
xnumpy = x.numpy()
plt.plot(xnumpy, U_pred[:, 0], 'o', markersize=1)
plt.plot(xnumpy, U_pred[:, 20], 'o', markersize=1)
plt.plot(xnumpy, U_pred[:, 40], 'o', markersize=1)
plt.figure(figsize=(5, 3), dpi=300)
sns.heatmap(U_pred, cmap='jet')
plt.show()

参考文献

[1] M. Raissi a, et al. “Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations.” Journal of Computational Physics, Academic Press, 3 Nov. 2018, www.sciencedirect.com/science/article/pii/S0021999118307125.