1379. 找出克隆二叉树中的相同节点
给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 original 中的目标节点 target。
其中,克隆树 cloned 是原始树 original 的一个 副本 。
请找出在树 cloned 中,与 target 相同 的节点,并返回对该节点的引用(在 C/C++ 等有指针的语言中返回 节点指针,其他语言返回节点本身)。
注意:你 不能 对两棵二叉树,以及 target 节点进行更改。只能 返回对克隆树 cloned 中已有的节点的引用。
示例 1:
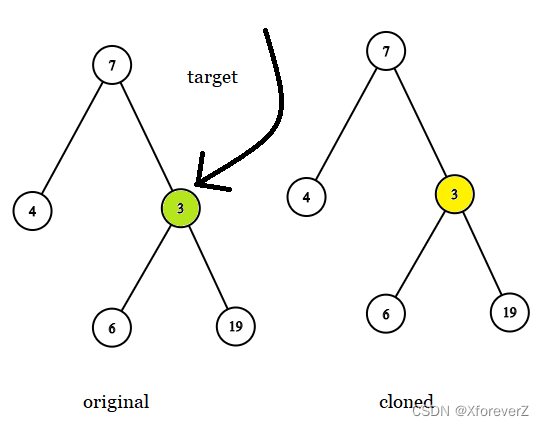
输入: tree = [7,4,3,null,null,6,19], target = 3
输出: 3
解释: 上图画出了树 original 和 cloned。target 节点在树 original 中,用绿色标记。答案是树 cloned 中的黄颜色的节点(其他示例类似)。
示例 2:

输入: tree = [7], target = 7
输出: 7
示例 3:

输入: tree = [8,null,6,null,5,null,4,null,3,null,2,null,1], target = 4
输出: 4
提示:
树中节点的数量范围为 [1, 104] 。
同一棵树中,没有值相同的节点。
target 节点是树 original 中的一个节点,并且不会是 null 。
进阶:如果树中允许出现值相同的节点,将如何解答?
递归即可:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {
public:TreeNode* getTargetCopy(TreeNode* original, TreeNode* cloned,TreeNode* target) {if (original == NULL) {return NULL;}if (original == target) {return cloned;}TreeNode* res = getTargetCopy(original->left, cloned->left, target);if (res != NULL) {return res;}return getTargetCopy(original->right, cloned->right, target);}
};
2192. 有向无环图中一个节点的所有祖先
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
示例 1:
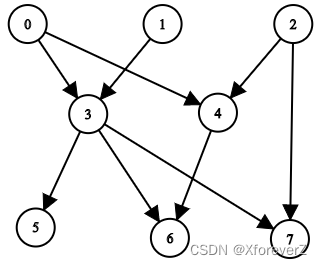
输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 ,1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ,1 和 3 。
- 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。
- 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
示例 2:
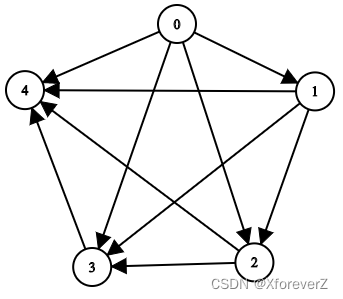
输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ,1 和 2 。
- 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
提示:
1 <= n <= 1000
0 <= edges.length <= min(2000, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi <= n - 1
fromi != toi
图中不会有重边。
图是 有向 且 无环 的。
逆向dfs(菜狗不会,抄的灵神):
class Solution {
public:vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {vector<vector<int>> g(n);for (auto& e : edges) {g[e[1]].push_back(e[0]); // 反向建图}vector<vector<int>> ans(n);vector<int> vis(n);function<void(int)> dfs = [&](int x) {vis[x] = true; // 避免重复访问for (int y : g[x]) {if (!vis[y]) {dfs(y); // 只递归没有访问过的点}}};for (int i = 0; i < n; i++) {ranges::fill(vis, false);dfs(i); // 从 i 开始 DFSvis[i] = false; // ans[i] 不含 ifor (int j = 0; j < n; j++) {if (vis[j]) {ans[i].push_back(j);}}}return ans;}
};
题解:两种方法:逆向/正向
1026. 节点与其祖先之间的最大差值
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例 1:
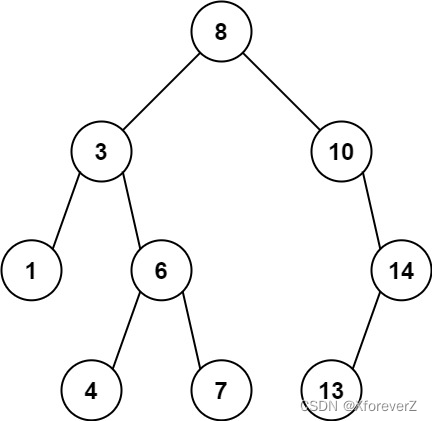
输入:root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出:7
解释:
我们有大量的节点与其祖先的差值,其中一些如下:
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
示例 2:
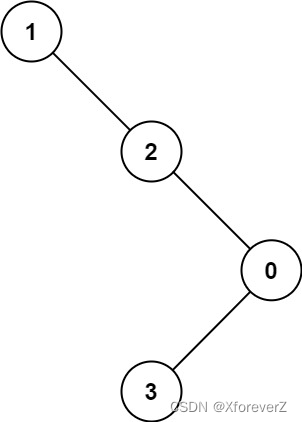
输入:root = [1,null,2,null,0,3]
输出:3
提示:
树中的节点数在 2 到 5000 之间。
0 <= Node.val <= 1e5
DFS:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:int maxAncestorDiff(TreeNode* root) {return dfs(root, root->val, root->val);}private:int dfs(TreeNode* node, int mn, int mx) {if (!node) {return mx - mn;}mx = max(mx, node->val);mn = min(mn, node->val);return max(dfs(node->left, mn, mx), dfs(node->right, mn, mx));}
};1483. 树节点的第 K 个祖先(Hard)
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。
树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。
实现 TreeAncestor 类:
TreeAncestor(int n, int[] parent) 对树和父数组中的节点数初始化对象。
getKthAncestor(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点,返回 -1 。
示例 1:
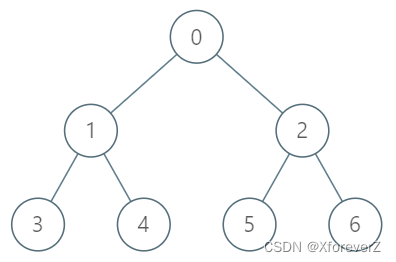
输入:
[“TreeAncestor”,“getKthAncestor”,“getKthAncestor”,“getKthAncestor”]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
输出:
[null,1,0,-1]
解释:
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点
提示:
1 <= k <= n <= 5 * 104
parent[0] == -1 表示编号为 0 的节点是根节点。
对于所有的 0 < i < n ,0 <= parent[i] < n 总成立
0 <= node < n
至多查询 5 * 1e4 次
看题解是acm的板子题,菜鸡不会(orz)
class TreeAncestor {private:vector<vector<int>> dp;public:TreeAncestor(int n, vector<int>& parent) : dp(n) {for (int i = 0; i < n; i++)dp[i].push_back(parent[i]);for (int j = 1;; j++) {bool allneg = true;for (int i = 0; i < n; i++) {int t = dp[i][j - 1] != -1 ? dp[dp[i][j - 1]][j - 1] : -1;dp[i].push_back(t);if (t != -1)allneg = false;}if (allneg)break; // 所有的节点的 2^j 的祖先都是 -1 了,就不用再计算了}}int getKthAncestor(int node, int k) {if (k == 0 || node == -1)return node;int pos =ffs(k) -1; // C++ 语言中 ffs(k) 求解出 k 的最右侧第一个 1 的位置(1-based)return pos < dp[node].size()? getKthAncestor(dp[node][pos], k - (1 << pos)): -1;}
};
是另外的大佬的题解:
力扣在逐渐把 ACM 模板题搬上来,这个问题是 Binary Lifting
1600. 王位继承顺序
一个王国里住着国王、他的孩子们、他的孙子们等等。每一个时间点,这个家庭里有人出生也有人死亡。
这个王国有一个明确规定的王位继承顺序,第一继承人总是国王自己。我们定义递归函数 Successor(x, curOrder) ,给定一个人 x 和当前的继承顺序,该函数返回 x 的下一继承人。
Successor(x, curOrder):
如果 x 没有孩子或者所有 x 的孩子都在 curOrder 中:
如果 x 是国王,那么返回 null
否则,返回 Successor(x 的父亲, curOrder)
否则,返回 x 不在 curOrder 中最年长的孩子
比方说,假设王国由国王,他的孩子 Alice 和 Bob (Alice 比 Bob 年长)和 Alice 的孩子 Jack 组成。
一开始, curOrder 为 [“king”].
调用 Successor(king, curOrder) ,返回 Alice ,所以我们将 Alice 放入 curOrder 中,得到 [“king”, “Alice”] 。
调用 Successor(Alice, curOrder) ,返回 Jack ,所以我们将 Jack 放入 curOrder 中,得到 [“king”, “Alice”, “Jack”] 。
调用 Successor(Jack, curOrder) ,返回 Bob ,所以我们将 Bob 放入 curOrder 中,得到 [“king”, “Alice”, “Jack”, “Bob”] 。
调用 Successor(Bob, curOrder) ,返回 null 。最终得到继承顺序为 [“king”, “Alice”, “Jack”, “Bob”] 。
通过以上的函数,我们总是能得到一个唯一的继承顺序。
请你实现 ThroneInheritance 类:
ThroneInheritance(string kingName) 初始化一个 ThroneInheritance 类的对象。国王的名字作为构造函数的参数传入。
void birth(string parentName, string childName) 表示 parentName 新拥有了一个名为 childName 的孩子。
void death(string name) 表示名为 name 的人死亡。一个人的死亡不会影响 Successor 函数,也不会影响当前的继承顺序。你可以只将这个人标记为死亡状态。
string[] getInheritanceOrder() 返回 除去 死亡人员的当前继承顺序列表。
示例:
输入:
[“ThroneInheritance”, “birth”, “birth”, “birth”, “birth”, “birth”, “birth”, “getInheritanceOrder”, “death”, “getInheritanceOrder”]
[[“king”], [“king”, “andy”], [“king”, “bob”], [“king”, “catherine”], [“andy”, “matthew”], [“bob”, “alex”], [“bob”, “asha”], [null], [“bob”], [null]]
输出:
[null, null, null, null, null, null, null, [“king”, “andy”, “matthew”, “bob”, “alex”, “asha”, “catherine”], null, [“king”, “andy”, “matthew”, “alex”, “asha”, “catherine”]]
解释:
ThroneInheritance t= new ThroneInheritance(“king”); // 继承顺序:king
t.birth(“king”, “andy”); // 继承顺序:king > andy
t.birth(“king”, “bob”); // 继承顺序:king > andy > bob
t.birth(“king”, “catherine”); // 继承顺序:king > andy > bob > catherine
t.birth(“andy”, “matthew”); // 继承顺序:king > andy > matthew > bob > catherine
t.birth(“bob”, “alex”); // 继承顺序:king > andy > matthew > bob > alex > catherine
t.birth(“bob”, “asha”); // 继承顺序:king > andy > matthew > bob > alex > asha > catherine
t.getInheritanceOrder(); // 返回 [“king”, “andy”, “matthew”, “bob”, “alex”, “asha”, “catherine”]
t.death(“bob”); // 继承顺序:king > andy > matthew > bob(已经去世)> alex > asha > catherine
t.getInheritanceOrder(); // 返回 [“king”, “andy”, “matthew”, “alex”, “asha”, “catherine”]
提示:
1 <= kingName.length, parentName.length, childName.length, name.length <= 15
kingName,parentName, childName 和 name 仅包含小写英文字母。
所有的参数 childName 和 kingName 互不相同。
所有 death 函数中的死亡名字 name 要么是国王,要么是已经出生了的人员名字。
每次调用 birth(parentName, childName) 时,测试用例都保证 parentName 对应的人员是活着的。
最多调用 105 次birth 和 death 。
最多调用 10 次 getInheritanceOrder 。
哈希建树,前序遍历:
class ThroneInheritance {unordered_map<string, vector<string>> edges;unordered_set<string> dead;string king;public:ThroneInheritance(string kingName) { king = kingName; }void birth(string parentName, string childName) {edges[parentName].push_back(childName);}void death(string name) { dead.insert(name); }vector<string> getInheritanceOrder() {vector<string> ans;preorder(ans, king);return ans;}void preorder(vector<string>& ans, string name) {if (!dead.count(name)) {ans.push_back(name);}for (const string& childName : edges[name]) {preorder(ans, childName);}}
};/*** Your ThroneInheritance object will be instantiated and called as such:* ThroneInheritance* obj = new ThroneInheritance(kingName);* obj->birth(parentName,childName);* obj->death(name);* vector<string> param_3 = obj->getInheritanceOrder();*/
2009. 使数组连续的最少操作数(Hard)
给你一个整数数组 nums 。每一次操作中,你可以将 nums 中 任意 一个元素替换成 任意 整数。
如果 nums 满足以下条件,那么它是 连续的 :
nums 中所有元素都是 互不相同 的。
nums 中 最大 元素与 最小 元素的差等于 nums.length - 1 。
比方说,nums = [4, 2, 5, 3] 是 连续的 ,但是 nums = [1, 2, 3, 5, 6] 不是连续的 。
请你返回使 nums 连续 的 最少 操作次数。
示例 1:
输入:nums = [4,2,5,3]
输出:0
解释:nums 已经是连续的了。
示例 2:
输入:nums = [1,2,3,5,6]
输出:1
解释:一个可能的解是将最后一个元素变为 4 。
结果数组为 [1,2,3,5,4] ,是连续数组。
示例 3:
输入:nums = [1,10,100,1000]
输出:3
解释:一个可能的解是:
- 将第二个元素变为 2 。
- 将第三个元素变为 3 。
- 将第四个元素变为 4 。
结果数组为 [1,2,3,4] ,是连续数组。
提示:
1 <= nums.length <= 1e5
1 <= nums[i] <= 1e9
滑动窗口,当时做这题没想到方法wa了好多次,思维比肌肉记忆更重要:
class Solution {
public:int minOperations(vector<int>& nums) {ranges::sort(nums);int n = nums.size();int m = unique(nums.begin(), nums.end()) - nums.begin();int ans = 0, left = 0;for (int i = 0; i < m; i++) {while (nums[left] < nums[i] - n + 1) {left++;}ans = max(ans, i - left + 1);}return n - ans;}
};
2529. 正整数和负整数的最大计数
给你一个按 非递减顺序 排列的数组 nums ,返回正整数数目和负整数数目中的最大值。
换句话讲,如果 nums 中正整数的数目是 pos ,而负整数的数目是 neg ,返回 pos 和 neg二者中的最大值。
注意:0 既不是正整数也不是负整数。
示例 1:
输入:nums = [-2,-1,-1,1,2,3]
输出:3
解释:共有 3 个正整数和 3 个负整数。计数得到的最大值是 3 。
示例 2:
输入:nums = [-3,-2,-1,0,0,1,2]
输出:3
解释:共有 2 个正整数和 3 个负整数。计数得到的最大值是 3 。
示例 3:
输入:nums = [5,20,66,1314]
输出:4
解释:共有 4 个正整数和 0 个负整数。计数得到的最大值是 4 。
提示:
1 <= nums.length <= 2000
-2000 <= nums[i] <= 2000
nums 按 非递减顺序 排列。
进阶:你可以设计并实现时间复杂度为 O(log(n)) 的算法解决此问题吗?
二分:
class Solution {
public:int maximumCount(vector<int>& nums) {int left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < 0) {left = mid + 1;} else {right = mid;}}int negCount = left;left = 0, right = nums.size();while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] <= 0) {left = mid + 1;} else {right = mid;}}int posCount = nums.size() - left;return max(negCount, posCount);}
};但是看了灵神题解后发现他的真的很简洁:
class Solution {
public:int maximumCount(vector<int> &nums) {int neg = 0, pos = 0;for (int x : nums) {if (x < 0) {neg++;} else if (x > 0) {pos++;}}return max(neg, pos);}
};
题解:两种方法:遍历 / 二分查找(Python/Java/C++/Go/JS/Rust)
1702. 修改后的最大二进制字符串
给你一个二进制字符串 binary ,它仅有 0 或者 1 组成。你可以使用下面的操作任意次对它进行修改:
操作 1 :如果二进制串包含子字符串 “00” ,你可以用 “10” 将其替换。
比方说, “00010” -> “10010”
操作 2 :如果二进制串包含子字符串 “10” ,你可以用 “01” 将其替换。
比方说, “00010” -> “00001”
请你返回执行上述操作任意次以后能得到的 最大二进制字符串 。如果二进制字符串 x 对应的十进制数字大于二进制字符串 y 对应的十进制数字,那么我们称二进制字符串 x 大于二进制字符串 y 。
示例 1:
输入:binary = “000110”
输出:“111011”
解释:一个可行的转换为:
“000110” -> “000101”
“000101” -> “100101”
“100101” -> “110101”
“110101” -> “110011”
“110011” -> “111011”
示例 2:
输入:binary = “01”
输出:“01”
解释:“01” 没办法进行任何转换。
提示:
1 <= binary.length <= 105
binary 仅包含 ‘0’ 和 ‘1’ 。
模拟贪心:
class Solution {
public:string maximumBinaryString(string binary) {int n = binary.size();int j = 0;for (int i = 0; i < n; i++) {if (binary[i] == '0') {while (j <= i || (j < n && binary[j] == '1')) {j++;}if (j < n) {binary[j] = '1';binary[i] = '1';binary[i + 1] = '0';}}}return binary;}
};
1766. 互质树
给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。
给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值,edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。
当 gcd(x, y) == 1 ,我们称两个数 x 和 y 是 互质的 ,其中 gcd(x, y) 是 x 和 y 的 最大公约数 。
从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。
请你返回一个大小为 n 的数组 ans ,其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ,如果不存在这样的祖先节点,ans[i] 为 -1 。
示例 1:
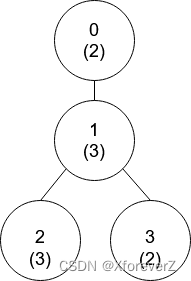
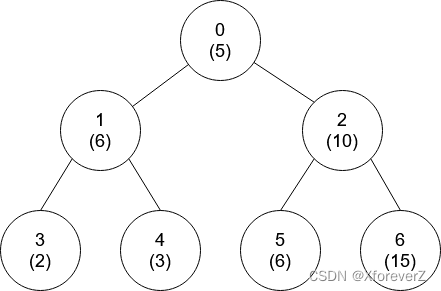
输入:nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出:[-1,0,0,1]
解释:上图中,每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的(gcd(2,3) == 1)。
- 节点 2 有两个祖先节点,分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的(gcd(3,3) == 3)但节点 0 的值是互质的(gcd(2,3) == 1),所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点,分别是节点 1 和节点 0 。它与节点 1 互质(gcd(3,2) == 1),所以节点 1 是离它最近的符合要求的祖先节点。
示例 2:
输入:nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:[-1,0,-1,0,0,0,-1]
提示:
nums.length == n
1 <= nums[i] <= 50
1 <= n <= 105
edges.length == n - 1
edges[j].length == 2
0 <= uj, vj < n
uj != vj
DFS回溯,抄的灵神题解:
const int MX = 51;
vector<int> coprime[MX];auto init = [] {// 预处理:coprime[i] 保存 [1, MX) 中与 i 互质的所有元素for (int i = 1; i < MX; i++) {for (int j = 1; j < MX; j++) {if (gcd(i, j) == 1) {coprime[i].push_back(j);}}}return 0;
}();class Solution {vector<vector<int>> g;vector<int> ans;pair<int, int> val_depth_id[MX]; // 包含深度和节点编号void dfs(int x, int fa, int depth, vector<int> &nums) {int val = nums[x]; // x 的节点值// 计算与 val 互质的数中,深度最大的节点编号int max_depth = 0;for (int j : coprime[val]) {auto [depth, id] = val_depth_id[j];if (depth > max_depth) {max_depth = depth;ans[x] = id;}}auto tmp = val_depth_id[val]; // 用于恢复现场val_depth_id[val] = {depth, x}; // 保存 val 对应的节点深度和节点编号for (int y : g[x]) {if (y != fa) {dfs(y, x, depth + 1, nums);}}val_depth_id[val] = tmp; // 恢复现场}public:vector<int> getCoprimes(vector<int> &nums, vector<vector<int>> &edges) {int n = nums.size();g.resize(n);for (auto &e : edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}ans.resize(n, -1);dfs(0, -1, 1, nums);return ans;}
};
DFS 中记录节点值的深度和编号,回溯写法
学到了学到了
2923. 找到冠军 I
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。
给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j :如果 grid[i][j] == 1,那么 i 队比 j 队 强 ;否则,j 队比 i 队 强 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
返回这场比赛中将会成为冠军的队伍。
示例 1:
输入:grid = [[0,1],[0,0]]
输出:0
解释:比赛中有两支队伍。
grid[0][1] == 1 表示 0 队比 1 队强。所以 0 队是冠军。
示例 2:
输入:grid = [[0,0,1],[1,0,1],[0,0,0]]
输出:1
解释:比赛中有三支队伍。
grid[1][0] == 1 表示 1 队比 0 队强。
grid[1][2] == 1 表示 1 队比 2 队强。
所以 1 队是冠军。
提示:
n == grid.length
n == grid[i].length
2 <= n <= 100
grid[i][j] 的值为 0 或 1
对于所有 i, grid[i][i] 等于 0.
对于满足 i != j 的所有 i, j ,grid[i][j] != grid[j][i] 均成立
生成的输入满足:如果 a 队比 b 队强,b 队比 c 队强,那么 a 队比 c 队强
暴力即可:
class Solution {
public:int findChampion(vector<vector<int>>& grid) {int ans = 0;for (int i = 1; i < grid.size(); i++) {if (grid[i][ans]) {ans = i;}}return ans;}
};2924. 找到冠军 II
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。每支队伍也是 有向无环图(DAG) 上的一个节点。
给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图,其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。
从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ,也就是 b 队比 a 队 弱 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
如果这场比赛存在 唯一 一个冠军,则返回将会成为冠军的队伍。否则,返回 -1 。
注意
环 是形如 a1, a2, …, an, an+1 的一个序列,且满足:节点 a1 与节点 an+1 是同一个节点;节点 a1, a2, …, an 互不相同;对于范围 [1, n] 中的每个 i ,均存在一条从节点 ai 到节点 ai+1 的有向边。
有向无环图 是不存在任何环的有向图。
示例 1:
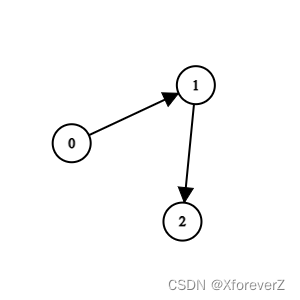
输入:n = 3, edges = [[0,1],[1,2]]
输出:0
解释:1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。
示例 2:
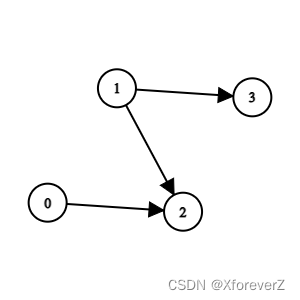
输入:n = 4, edges = [[0,2],[1,3],[1,2]]
输出:-1
解释:2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。
提示:
1 <= n <= 100
m == edges.length
0 <= m <= n * (n - 1) / 2
edges[i].length == 2
0 <= edge[i][j] <= n - 1
edges[i][0] != edges[i][1]
生成的输入满足:如果 a 队比 b 队强,就不存在 b 队比 a 队强
生成的输入满足:如果 a 队比 b 队强,b 队比 c 队强,那么 a 队比 c 队强
直接遍历:
class Solution {
public:int findChampion(int n, vector<vector<int>>& edges) {vector<int> indegree(n, 0);for (const auto& edge : edges) {indegree[edge[1]]++;}int champion = -1;for (int i = 0; i < n; ++i) {if (indegree[i] == 0) {if (champion != -1) {return -1;}champion = i;}}return champion;}
};705. 设计哈希集合
不使用任何内建的哈希表库设计一个哈希集合(HashSet)。
实现 MyHashSet 类:
void add(key) 向哈希集合中插入值 key 。
bool contains(key) 返回哈希集合中是否存在这个值 key 。
void remove(key) 将给定值 key 从哈希集合中删除。如果哈希集合中没有这个值,什么也不做。
示例:
输入:
[“MyHashSet”, “add”, “add”, “contains”, “contains”, “add”, “contains”, “remove”, “contains”]
[[], [1], [2], [1], [3], [2], [2], [2], [2]]
输出:
[null, null, null, true, false, null, true, null, false]
解释:
MyHashSet myHashSet = new MyHashSet();
myHashSet.add(1); // set = [1]
myHashSet.add(2); // set = [1, 2]
myHashSet.contains(1); // 返回 True
myHashSet.contains(3); // 返回 False ,(未找到)
myHashSet.add(2); // set = [1, 2]
myHashSet.contains(2); // 返回 True
myHashSet.remove(2); // set = [1]
myHashSet.contains(2); // 返回 False ,(已移除)
提示:
0 <= key <= 1e6
最多调用 1e4 次 add、remove 和 contains
HashSet基础:
class MyHashSet {
public:MyHashSet() { data = vector<bool>(1000001, false); }void add(int key) { data[key] = true; }void remove(int key) { data[key] = false; }bool contains(int key) { return data[key]; }private:vector<bool> data;
};/*** Your MyHashSet object will be instantiated and called as such:* MyHashSet* obj = new MyHashSet();* obj->add(key);* obj->remove(key);* bool param_3 = obj->contains(key);*/706. 设计哈希映射
不使用任何内建的哈希表库设计一个哈希映射(HashMap)。
实现 MyHashMap 类:
MyHashMap() 用空映射初始化对象
void put(int key, int value) 向 HashMap 插入一个键值对 (key, value) 。如果 key 已经存在于映射中,则更新其对应的值 value 。
int get(int key) 返回特定的 key 所映射的 value ;如果映射中不包含 key 的映射,返回 -1 。
void remove(key) 如果映射中存在 key 的映射,则移除 key 和它所对应的 value 。
示例:
输入:
[“MyHashMap”, “put”, “put”, “get”, “get”, “put”, “get”, “remove”, “get”]
[[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]]
输出:
[null, null, null, 1, -1, null, 1, null, -1]
解释:
MyHashMap myHashMap = new MyHashMap();
myHashMap.put(1, 1); // myHashMap 现在为 [[1,1]]
myHashMap.put(2, 2); // myHashMap 现在为 [[1,1], [2,2]]
myHashMap.get(1); // 返回 1 ,myHashMap 现在为 [[1,1], [2,2]]
myHashMap.get(3); // 返回 -1(未找到),myHashMap 现在为 [[1,1], [2,2]]
myHashMap.put(2, 1); // myHashMap 现在为 [[1,1], [2,1]](更新已有的值)
myHashMap.get(2); // 返回 1 ,myHashMap 现在为 [[1,1], [2,1]]
myHashMap.remove(2); // 删除键为 2 的数据,myHashMap 现在为 [[1,1]]
myHashMap.get(2); // 返回 -1(未找到),myHashMap 现在为 [[1,1]]
提示:
0 <= key, value <= 1e6
最多调用 1e4 次 put、get 和 remove 方法
同样的Hashset专题,基础:
class MyHashMap {
public:MyHashMap() {data = vector<int>(1000001 , -1);}void put(int key, int value) {data[key] = value;}int get(int key) {return data[key];}void remove(int key) {data[key] = -1;}private:vector<int> data;
};/*** Your MyHashMap object will be instantiated and called as such:* MyHashMap* obj = new MyHashMap();* obj->put(key,value);* int param_2 = obj->get(key);* obj->remove(key);*/
924. 尽量减少恶意软件的传播(Hard)
给出了一个由 n 个节点组成的网络,用 n × n 个邻接矩阵图 graph 表示。在节点网络中,当 graph[i][j] = 1 时,表示节点 i 能够直接连接到另一个节点 j。
一些节点 initial 最初被恶意软件感染。只要两个节点直接连接,且其中至少一个节点受到恶意软件的感染,那么两个节点都将被恶意软件感染。这种恶意软件的传播将继续,直到没有更多的节点可以被这种方式感染。
假设 M(initial) 是在恶意软件停止传播之后,整个网络中感染恶意软件的最终节点数。
如果从 initial 中移除某一节点能够最小化 M(initial), 返回该节点。如果有多个节点满足条件,就返回索引最小的节点。
请注意,如果某个节点已从受感染节点的列表 initial 中删除,它以后仍有可能因恶意软件传播而受到感染。
示例 1:
输入:graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
输出:0
示例 2:
输入:graph = [[1,0,0],[0,1,0],[0,0,1]], initial = [0,2]
输出:0
示例 3:
输入:graph = [[1,1,1],[1,1,1],[1,1,1]], initial = [1,2]
输出:1
提示:
n == graph.length
n == graph[i].length
2 <= n <= 300
graph[i][j] == 0 或 1.
graph[i][j] == graph[j][i]
graph[i][i] == 1
1 <= initial.length <= n
0 <= initial[i] <= n - 1
initial 中所有整数均不重复
DFS+并查集来做,虽然知道方法还是wa了10发,受不了了还是看了灵神题解:
class Solution {
public:int minMalwareSpread(vector<vector<int>>& graph, vector<int>& initial) {set<int> st(initial.begin(), initial.end());vector<int> vis(graph.size());int ans = -1, max_size = 0, node_id, size;function<void(int)> dfs = [&](int x) {vis[x] = true;size++;// 按照状态机更新 node_idif (node_id != -2 && st.contains(x)) {node_id = node_id == -1 ? x : -2;}for (int y = 0; y < graph[x].size(); y++) {if (graph[x][y] && !vis[y]) {dfs(y);}}};for (int x : initial) {if (vis[x]) {continue;}node_id = -1;size = 0;dfs(x);if (node_id >= 0 &&(size > max_size || size == max_size && node_id < ans)) {ans = node_id;max_size = size;}}return ans < 0 ? ranges::min(initial) : ans;}
};只包含一个被感染节点的最大连通块




![msyql中SQL 错误 [1118] [42000]: Row size too large (> 8126)](https://img-blog.csdnimg.cn/direct/246464b3a0ae4eed815d9a4f0054d0d0.png)





![基于JavaWeb开发的springboot网约车智能接单规划小程序[附源码]](https://img-blog.csdnimg.cn/direct/32156567858d455f8375fee65a47ed03.png)