机器学习算法——决策树算法详细解读

决策树（Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。

分类树（决策树）是一种十分常用的分类方法。它是一种监督学习，所谓监督学习就是给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。

这里引入一些标签，信息熵、信息增益、信息增益率、基尼系数，这些都是非常常用的必须背会

信息熵

信息熵是由克劳德·香农（Claude Shannon）在20世纪40年代提出的概念，它是信息论中的一个基本概念，用于描述信息的不确定度。信息熵的概念基于热力学中的熵，并将之应用于信息的量化度量。

信息熵通常用数学公式表示为( H(X) )，其中( X )代表一个随机变量，其取值有( n )种可能，每种取值的概率为( p(x_i) )，则( H(X) )的计算公式为

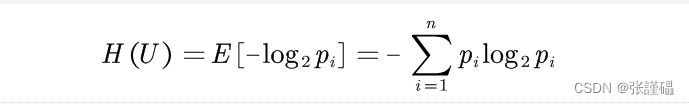
这个公式表明，一个事件的不确定性与该事件发生的概率有关，概率越小的事件发生时带来的信息量越大，反之亦然。

例如，如果在一个班级中随机抽取一名学生，如果抽取到的学生是天津大学或南开大学的学生，猜测正确的概率为0.5，此时的信息熵最高。而当提供更多关于学生的信息，如主修学科或内衣颜色，这些信息可以用来降低不确定性，从而影响信息熵。

信息熵在机器学习、数据压缩、密码学等领域有广泛应用，它帮助我们理解和量化数据中的不确定性。

信息增益

在概率论和信息论中，信息增益（information gain [2]）是非对称的，用以度量两种概率分布P和Q的差异。信息增益描述了当使用Q进行编码时，再使用P进行编码的差异。通常P代表样本或观察值的分布，也有可能是精确计算的理论分布。Q代表一种理论，模型，描述或者对P的近似。

H（A/B）是条件信息熵。

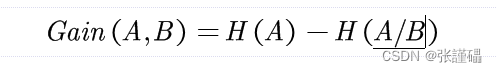
信息增益率

信息增益率是一种用于特征选择的指标，通常在决策树算法中使用。它结合了信息增益和特征的自身信息量，可以更好地处理特征取值较多的情况。

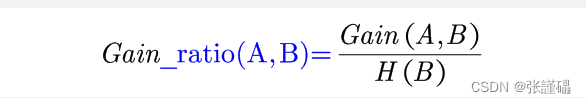
信息增益率是在，信息熵和信息增益的基础上进行求解的

基尼系数

基尼系数（英文：Gini index、Gini Coefficient），是国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标之一。其包括收入基尼系数（Income Gini）和财富基尼系数（Wealth Gini）。两者的算法大致相同，区别在于收入基尼系数的数据是来自于某地区的家庭收入统计，财富基尼系数的数据是来自于某地区的家庭总资产统计。

基尼系数最大为“1”，最小等于“0”。基尼系数越接近0表明收入分配越是趋向平等。国际上并没有一个组织或教科书给出最适合的基尼系数标准。但有不少人认为基尼系数小于0.2时，居民收入过于平均，0.2-0.3之间时较为平均，0.3-0.4之间时比较合理，0.4-0.5时差距过大，大于0.5时差距悬殊。

基尼系数最早由意大利统计与社会学家Corrado Gini在1912年提出。据中国国家统计局的数据，用于描绘收入差距的基尼系数自2000年开始就越过了0.4的警戒线，并且直到2009年呈上升趋势，2009-2012年呈下降趋势，并在2013年至今稳定于0.47，仅在2015年降至0.46。

决策树常用的算法都是，ID3、C4.5、CART

数据展示：

sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
5 5.4 3.9 1.7 0.4
6 4.6 3.4 1.4 0.3
7 5.0 3.4 1.5 0.2
8 4.4 2.9 1.4 0.2
9 4.9 3.1 1.5 0.1
10 5.4 3.7 1.5 0.2
11 4.8 3.4 1.6 0.2
12 4.8 3.0 1.4 0.1
13 4.3 3.0 1.1 0.1
14 5.8 4.0 1.2 0.2
15 5.7 4.4 1.5 0.4
16 5.4 3.9 1.3 0.4
17 5.1 3.5 1.4 0.3
18 5.7 3.8 1.7 0.3
19 5.1 3.8 1.5 0.3
20 5.4 3.4 1.7 0.2
21 5.1 3.7 1.5 0.4
22 4.6 3.6 1.0 0.2
23 5.1 3.3 1.7 0.5
24 4.8 3.4 1.9 0.2
25 5.0 3.0 1.6 0.2
26 5.0 3.4 1.6 0.4
27 5.2 3.5 1.5 0.2
28 5.2 3.4 1.4 0.2
29 4.7 3.2 1.6 0.2
30 4.8 3.1 1.6 0.2
31 5.4 3.4 1.5 0.4
32 5.2 4.1 1.5 0.1
33 5.5 4.2 1.4 0.2
34 4.9 3.1 1.5 0.2
35 5.0 3.2 1.2 0.2
36 5.5 3.5 1.3 0.2
37 4.9 3.6 1.4 0.1
38 4.4 3.0 1.3 0.2
39 5.1 3.4 1.5 0.2
40 5.0 3.5 1.3 0.3
41 4.5 2.3 1.3 0.3
42 4.4 3.2 1.3 0.2
43 5.0 3.5 1.6 0.6
44 5.1 3.8 1.9 0.4
45 4.8 3.0 1.4 0.3
46 5.1 3.8 1.6 0.2
47 4.6 3.2 1.4 0.2
48 5.3 3.7 1.5 0.2
49 5.0 3.3 1.4 0.2
50 7.0 3.2 4.7 1.4
51 6.4 3.2 4.5 1.5
52 6.9 3.1 4.9 1.5
53 5.5 2.3 4.0 1.3
54 6.5 2.8 4.6 1.5
55 5.7 2.8 4.5 1.3
56 6.3 3.3 4.7 1.6
57 4.9 2.4 3.3 1.0
58 6.6 2.9 4.6 1.3
59 5.2 2.7 3.9 1.4
60 5.0 2.0 3.5 1.0
61 5.9 3.0 4.2 1.5
62 6.0 2.2 4.0 1.0
63 6.1 2.9 4.7 1.4
64 5.6 2.9 3.6 1.3
65 6.7 3.1 4.4 1.4
66 5.6 3.0 4.5 1.5
67 5.8 2.7 4.1 1.0
68 6.2 2.2 4.5 1.5
69 5.6 2.5 3.9 1.1
70 5.9 3.2 4.8 1.8
71 6.1 2.8 4.0 1.3
72 6.3 2.5 4.9 1.5
73 6.1 2.8 4.7 1.2
74 6.4 2.9 4.3 1.3
75 6.6 3.0 4.4 1.4
76 6.8 2.8 4.8 1.4
77 6.7 3.0 5.0 1.7
78 6.0 2.9 4.5 1.5
79 5.7 2.6 3.5 1.0
80 5.5 2.4 3.8 1.1
81 5.5 2.4 3.7 1.0
82 5.8 2.7 3.9 1.2
83 6.0 2.7 5.1 1.6
84 5.4 3.0 4.5 1.5
85 6.0 3.4 4.5 1.6
86 6.7 3.1 4.7 1.5
87 6.3 2.3 4.4 1.3
88 5.6 3.0 4.1 1.3
89 5.5 2.5 4.0 1.3
90 5.5 2.6 4.4 1.2
91 6.1 3.0 4.6 1.4
92 5.8 2.6 4.0 1.2
93 5.0 2.3 3.3 1.0
94 5.6 2.7 4.2 1.3
95 5.7 3.0 4.2 1.2
96 5.7 2.9 4.2 1.3
97 6.2 2.9 4.3 1.3
98 5.1 2.5 3.0 1.1
99 5.7 2.8 4.1 1.3
100 6.3 3.3 6.0 2.5
101 5.8 2.7 5.1 1.9
102 7.1 3.0 5.9 2.1
103 6.3 2.9 5.6 1.8
104 6.5 3.0 5.8 2.2
105 7.6 3.0 6.6 2.1
106 4.9 2.5 4.5 1.7
107 7.3 2.9 6.3 1.8
108 6.7 2.5 5.8 1.8
109 7.2 3.6 6.1 2.5
110 6.5 3.2 5.1 2.0
111 6.4 2.7 5.3 1.9
112 6.8 3.0 5.5 2.1
113 5.7 2.5 5.0 2.0
114 5.8 2.8 5.1 2.4
115 6.4 3.2 5.3 2.3
116 6.5 3.0 5.5 1.8
117 7.7 3.8 6.7 2.2
118 7.7 2.6 6.9 2.3
119 6.0 2.2 5.0 1.5
120 6.9 3.2 5.7 2.3
121 5.6 2.8 4.9 2.0
122 7.7 2.8 6.7 2.0
123 6.3 2.7 4.9 1.8
124 6.7 3.3 5.7 2.1
125 7.2 3.2 6.0 1.8
126 6.2 2.8 4.8 1.8
127 6.1 3.0 4.9 1.8
128 6.4 2.8 5.6 2.1
129 7.2 3.0 5.8 1.6
130 7.4 2.8 6.1 1.9
131 7.9 3.8 6.4 2.0
132 6.4 2.8 5.6 2.2
133 6.3 2.8 5.1 1.5
134 6.1 2.6 5.6 1.4
135 7.7 3.0 6.1 2.3
136 6.3 3.4 5.6 2.4
137 6.4 3.1 5.5 1.8
138 6.0 3.0 4.8 1.8
139 6.9 3.1 5.4 2.1
140 6.7 3.1 5.6 2.4
141 6.9 3.1 5.1 2.3
142 5.8 2.7 5.1 1.9
143 6.8 3.2 5.9 2.3
144 6.7 3.3 5.7 2.5
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8

ID3代码

# 导入所需库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建ID3决策树模型
dt_classifier = DecisionTreeClassifier(criterion='entropy')  # 使用信息增益作为划分标准
dt_classifier.fit(X_train, y_train)# 可视化决策树
plt.figure(figsize=(10, 6))
plot_tree(dt_classifier, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

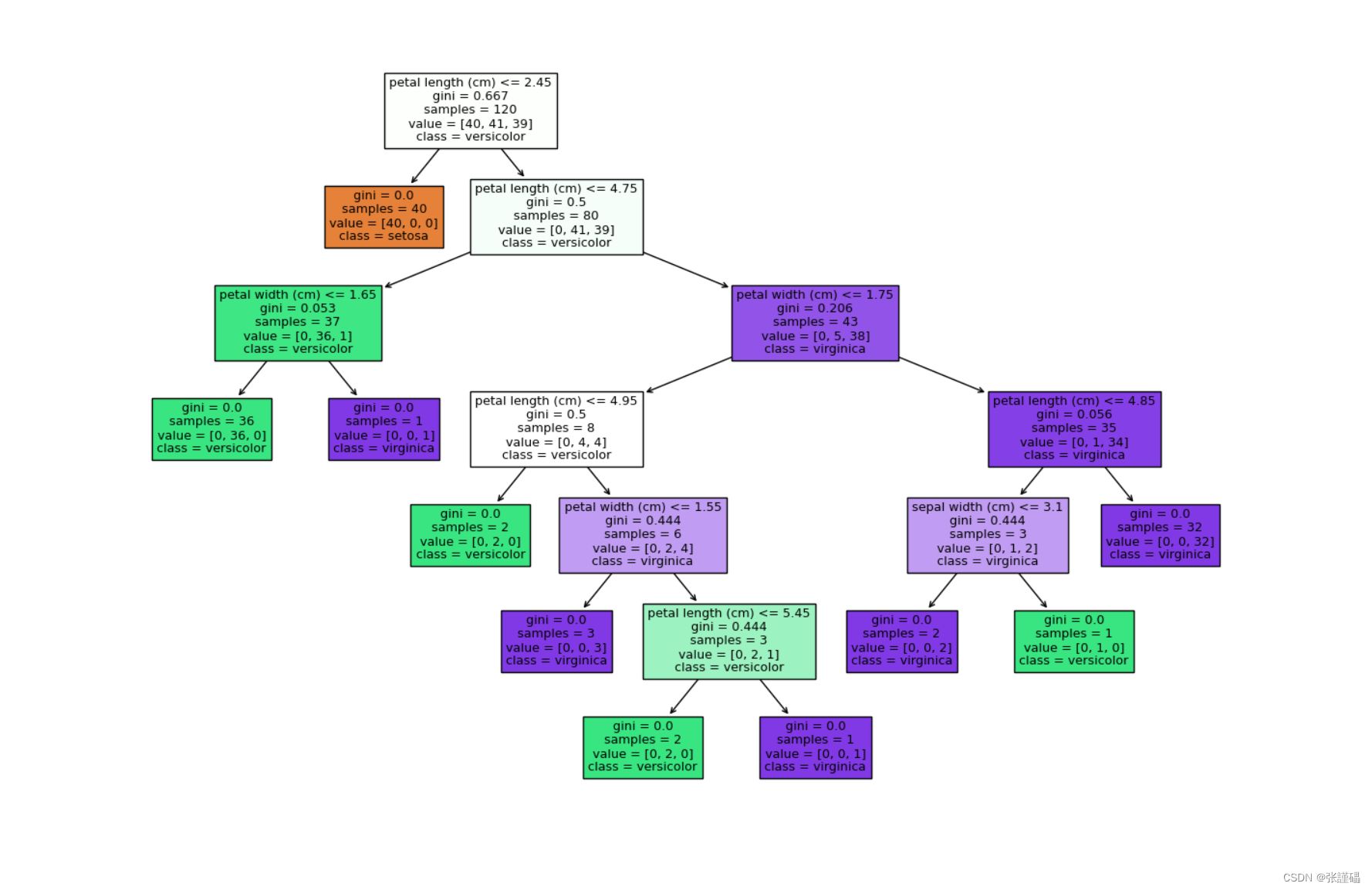
C4.5和CART算法这里引入了一个剪枝操作

剪枝

剪枝（pruning）的目的是为了避免决策树模型的过拟合。因为决策树算法在学习的过程中为了尽可能的正确的分类训练样本，不停地对结点进行划分，因此这会导致整棵树的分支过多，也就导致了过拟合。

可通过“剪枝”来一定程度避免因决策分支过多，以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合。

决策树的剪枝策略最基本的有两种：预剪枝（pre-pruning）和后剪枝（post-pruning）

预剪枝就是在构造决策树的过程中，先对每个结点在划分前进行估计，若果当前结点的划分不能带来决策树模型泛华性能的提升，则不对当前结点进行划分并且将当前结点标记为叶结点。

•优点
–降低过拟合风险
–显著减少训练时间和测试时间开销。
•缺点
–欠拟合风险：有些分支的当前划分虽然不能提升泛化性能，但在其基础上进行的后续划分却有可能显著提高性能。预剪枝基于 “ 贪心 ”本质禁止这些分支展开，带来了欠拟合风险。

后剪枝就是先把整颗决策树构造完毕，然后自底向上的对非叶结点进行考察，若将该结点对应的子树换为叶结点能够带来泛华性能的提升，则把该子树替换为叶结点。

•优点
后剪枝比预剪枝保留了更多的分支，欠拟合风险小，泛化性能往往优于预剪枝决策树
•缺点
训练时间开销大：后剪枝过程是在生成完全决策树之后进行的，需要自底向上对所有非叶结点逐一计算

C4.5是前剪枝，CART是后剪枝

C4.5代码

# 导入所需库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建C4.5决策树模型，并设置剪枝参数
dt_classifier = DecisionTreeClassifier(criterion='entropy', min_samples_split=3, min_samples_leaf=2)
dt_classifier.fit(X_train, y_train)# 可视化决策树
plt.figure(figsize=(20, 15))
plot_tree(dt_classifier, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

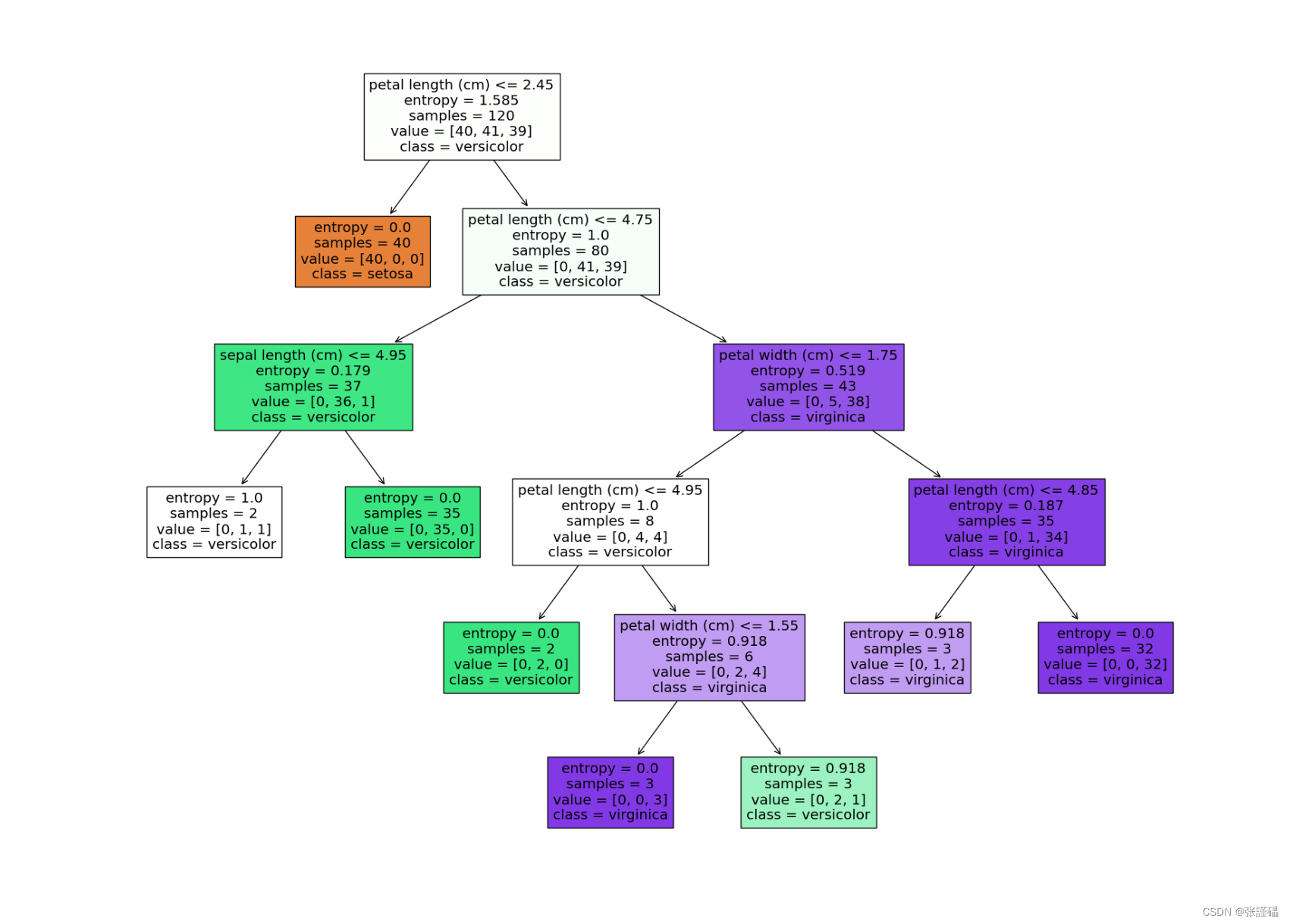
CART代码

# 导入所需库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 构建CART决策树模型，并设置剪枝参数
cart_classifier = DecisionTreeClassifier(criterion='gini', ccp_alpha=0.01)
cart_classifier.fit(X_train, y_train)# 可视化决策树
plt.figure(figsize=(20, 15))
plot_tree(cart_classifier, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()

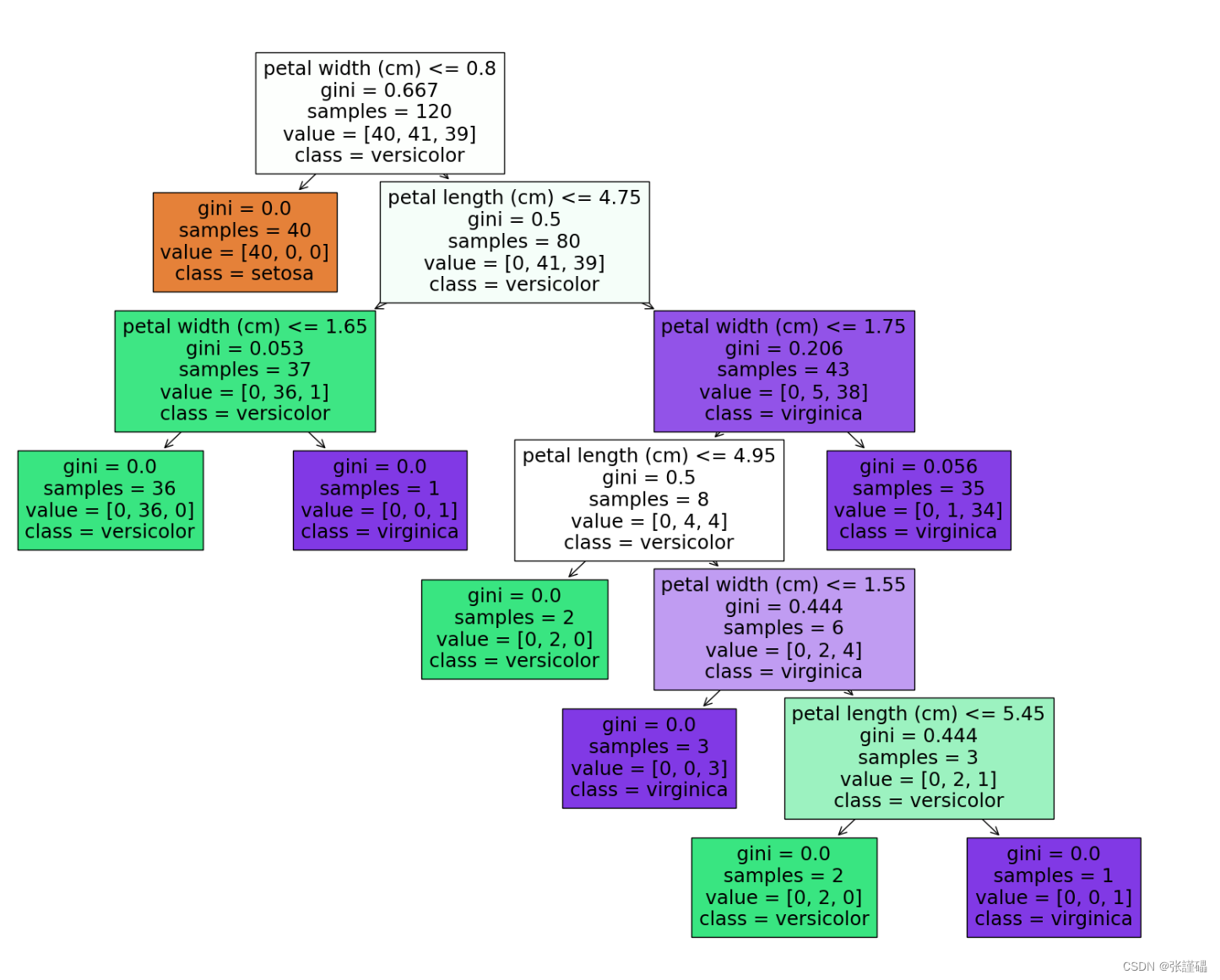
三种算法对比

分析鸾尾花数据集

代码

# 导入所需库
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt# 加载红酒数据集
wine = load_wine()
X = wine.data
y = wine.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化三个模型的准确率列表
accuracies = []# 循环遍历三种算法
for criterion in ['entropy', 'entropy', 'gini']:# 构建并训练决策树模型classifier = DecisionTreeClassifier(criterion=criterion)classifier.fit(X_train, y_train)# 在测试集上进行预测y_pred = classifier.predict(X_test)# 计算准确率并添加到准确率列表中accuracy = (y_pred == y_test).mean()accuracies.append(accuracy)# 绘制折线图
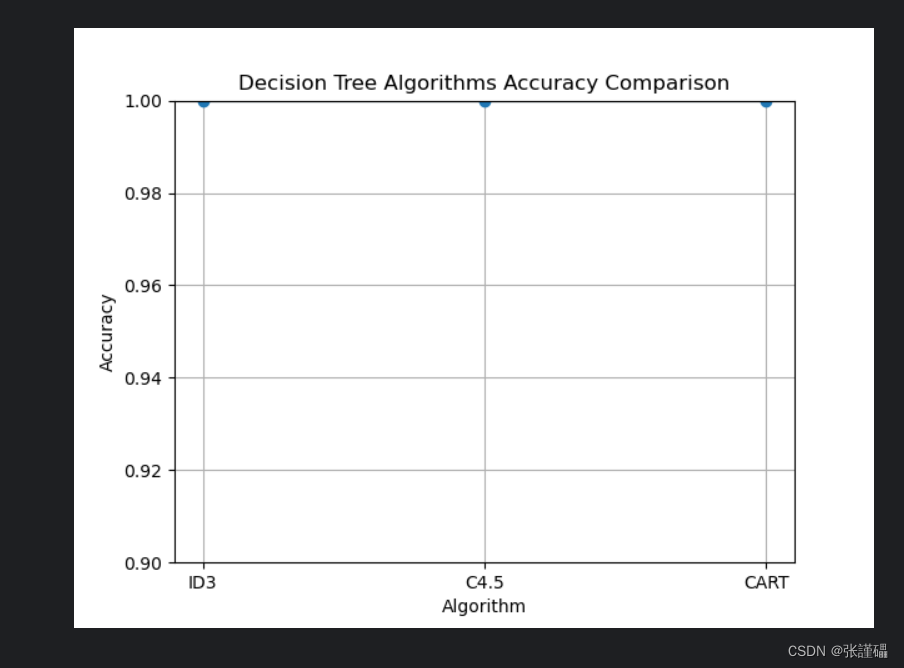
plt.plot(['ID3', 'C4.5', 'CART'], accuracies, marker='o')
plt.title('Decision Tree Algorithms Accuracy Comparison')
plt.xlabel('Algorithm')
plt.ylabel('Accuracy')
plt.ylim(0.9, 1.0)  # 设置y轴范围
plt.grid(True)
plt.show()

由于都是1.0的准确率，所有我们换一种数据集，我这里切换的是红酒品类数据集

# 导入所需库
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt# 加载红酒数据集
wine = load_wine()
X = wine.data
y = wine.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化三个模型的准确率列表和特征重要性列表
accuracies = []
feature_importances = []# 循环遍历三种算法
for criterion in ['entropy', 'entropy', 'gini']:# 构建并训练决策树模型classifier = DecisionTreeClassifier(criterion=criterion)classifier.fit(X_train, y_train)# 在测试集上进行预测y_pred = classifier.predict(X_test)# 计算准确率并添加到准确率列表中accuracy = (y_pred == y_test).mean()accuracies.append(accuracy)# 提取特征重要性并添加到列表中feature_importances.append(classifier.feature_importances_)# 绘制折线图
plt.figure(figsize=(20, 10))# 绘制准确率比较图
plt.subplot(1, 2, 1)
plt.plot(['ID3', 'C4.5', 'CART'], accuracies, marker='o')
plt.title('Decision Tree Algorithms Accuracy Comparison')
plt.xlabel('Algorithm')
plt.ylabel('Accuracy')
plt.ylim(0.9, 1.0)  # 设置y轴范围
plt.grid(True)# 绘制特征重要性图
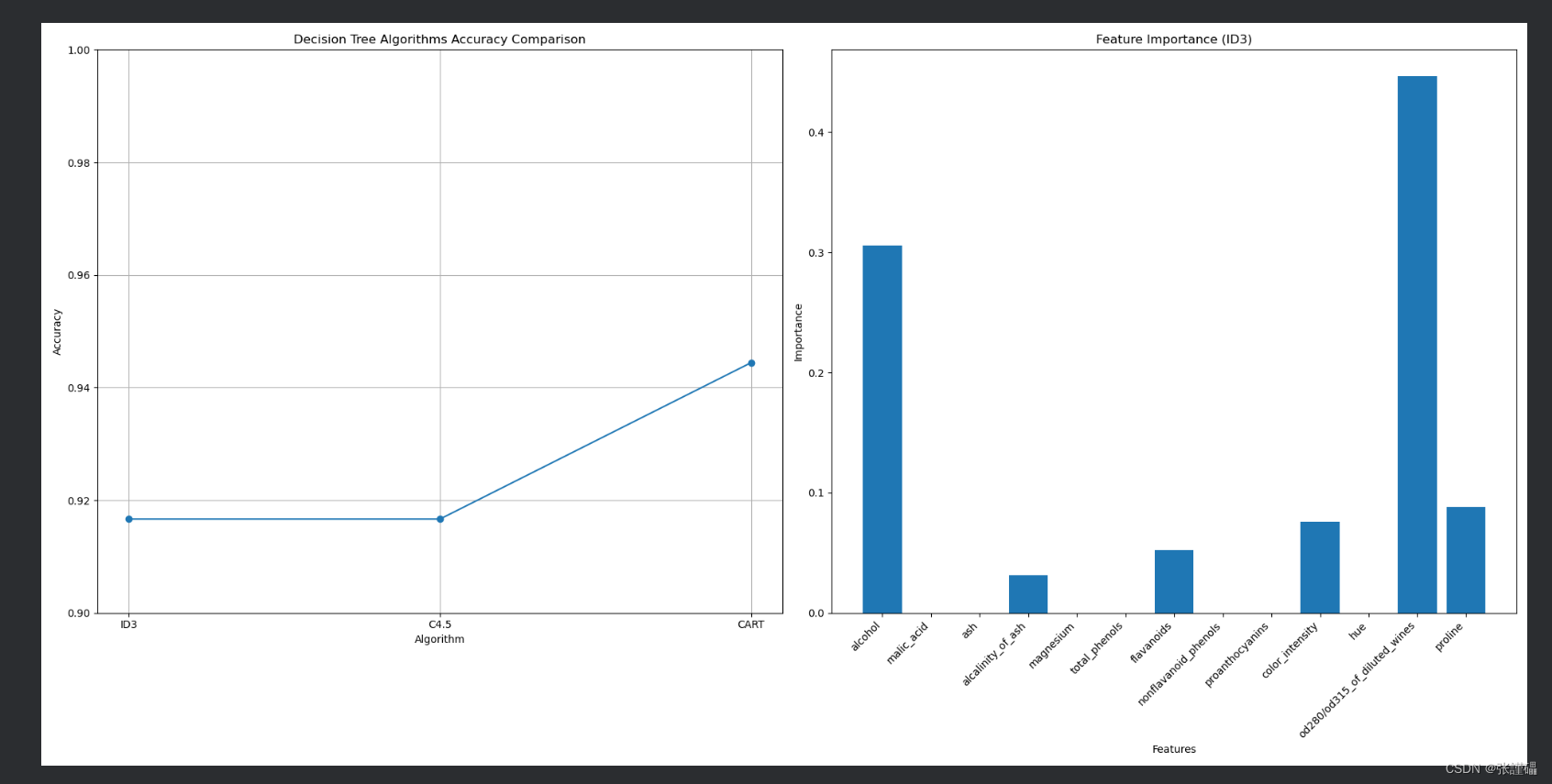
plt.subplot(1, 2, 2)
plt.bar(range(len(wine.feature_names)), feature_importances[0], tick_label=wine.feature_names)
plt.title('Feature Importance (ID3)')
plt.xlabel('Features')
plt.ylabel('Importance')plt.xticks(rotation=45, ha='right')  # 旋转x轴标签
plt.tight_layout()  # 调整布局以防止重叠
plt.show()

如果你能看到这里，并学会应用，恭喜你你的决策树算法，算是入门了

加油加油