1 基础内容

图没啥高深的，本质上就是个高级点的多叉树而已，适用于树的 DFS/BFS 遍历算法，全部适用于图。

1.1 图的表示

图的存储在算法题中常用邻接表和邻接矩阵表示：

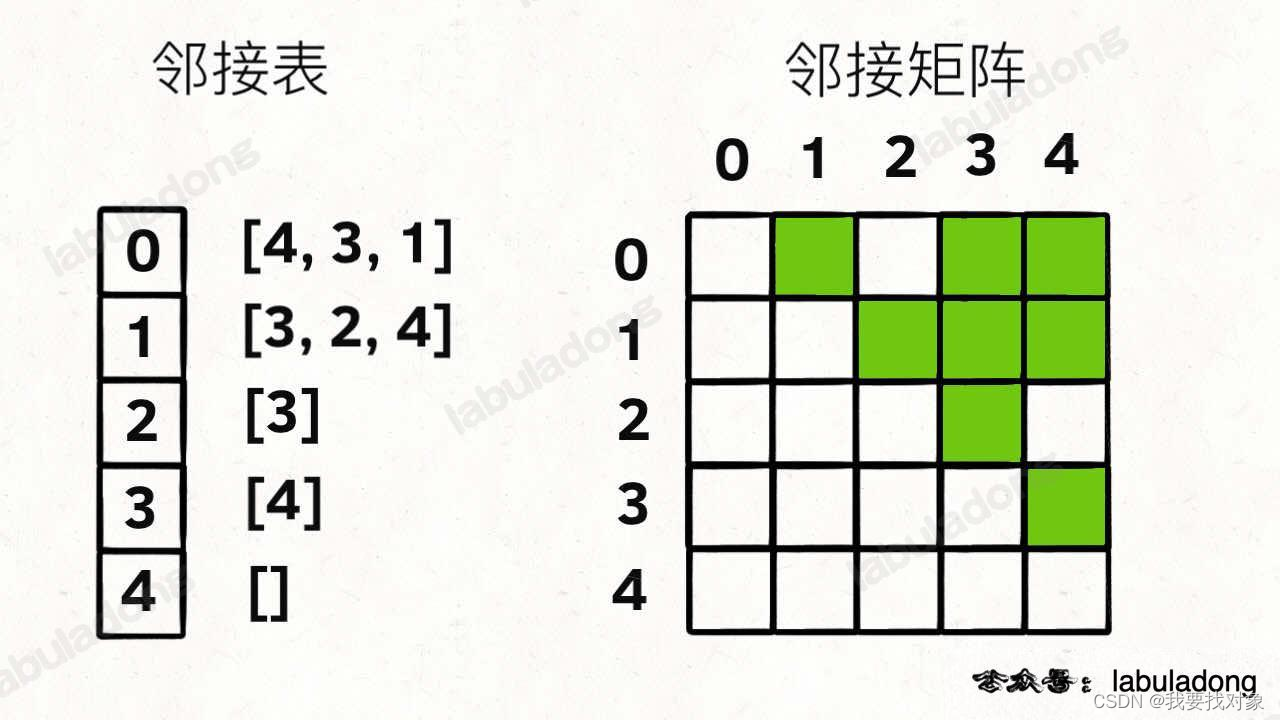
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

有向加权图怎么实现？很简单呀：
如果是邻接表，我们不仅仅存储某个节点 x 的所有邻居节点，还存储 x 到每个邻居的权重，不就实现加权有向图了吗？
如果是邻接矩阵，matrix[x][y] 不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重，不就变成加权有向图了吗？
如果用代码的形式来表现，大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
int[][] matrix;

1.2图的遍历

图怎么遍历？还是那句话，参考多叉树，多叉树的 DFS 遍历框架如下：

/* 多叉树遍历框架 */
void traverse(TreeNode root) {if (root == null) return;// 前序位置for (TreeNode child : root.children) {traverse(child);}// 后序位置
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况，从某个节点出发必然走到叶子节点，绝不可能回到它自身。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录在一次traverse中递归过的结点
boolean[] onPath;/* 图遍历框架 */
void traverse(Graph graph, int s) {if (visited[s]) return;// 经过节点 s，标记为已遍历visited[s] = true;// 做选择：标记节点 s 在路径上onPath[s] = true;for (int neighbor : graph.neighbors(s)) {traverse(graph, neighbor);}// 撤销选择：节点 s 离开路径onPath[s] = false;
}

注意 visited 数组和 onPath 数组的区别：
类比贪吃蛇游戏，visited 记录蛇经过过的格子，而 onPath 仅仅记录蛇身。在图的遍历过程中，onPath 用于判断是否成环，类比当贪吃蛇自己咬到自己（成环）的场景。
如果让你处理路径相关的问题，这个 onPath 变量是肯定会被用到的，比如 拓扑排序 中就有运用。
这个 onPath 数组的操作很像前文 回溯算法核心套路 中做「做选择」和「撤销选择」，区别在于位置：回溯算法的「做选择」和「撤销选择」在 for 循环里面，而对 onPath 数组的操作在 for 循环外面。

回忆：
对于回溯算法，我们需要在「树枝」上做选择和撤销选择：

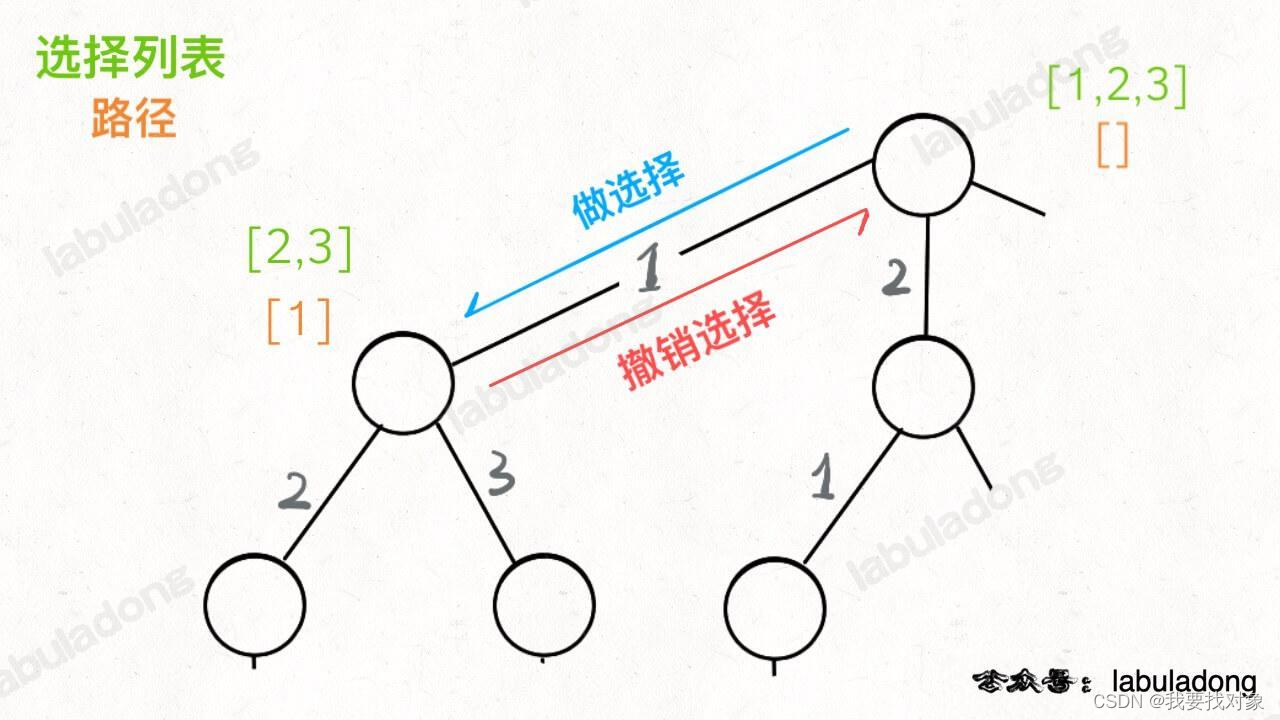
反映到代码上就是：

// DFS 算法，关注点在节点
void traverse(TreeNode root) {if (root == null) return;printf("进入节点 %s", root);for (TreeNode child : root.children) {traverse(child);}printf("离开节点 %s", root);
}// 回溯算法，关注点在树枝
void backtrack(TreeNode root) {if (root == null) return;for (TreeNode child : root.children) {// 做选择printf("从 %s 到 %s", root, child);backtrack(child);// 撤销选择printf("从 %s 到 %s", child, root);}
}

另一种解释就是，如果用回溯的方法遍历树，你会发现根节点被漏掉了：

void traverse(TreeNode root) {if (root == null) return;for (TreeNode child : root.children) {printf("进入节点 %s", child);traverse(child);printf("离开节点 %s", child);}
}

所以对于这里「图」的遍历，我们应该用 DFS 算法，即把 onPath 的操作放到 for 循环外面，否则会漏掉记录起始点的遍历。
说了这么多 onPath 数组，再说下 visited 数组，其目的很明显了，由于图可能含有环，visited 数组就是防止递归重复遍历同一个节点进入死循环的。

当然，如果题目告诉你图中不含环，可以把 visited 数组都省掉，基本就是多叉树的遍历。

2 例题

2.1 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）
graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）

示例1：

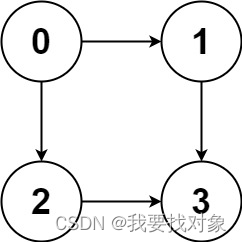
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

代码以及思路：
解法很简单，以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。
既然输入的图是无环的，我们就不需要 visited 数组辅助了，直接套用图的遍历框架：

class Solution {List<List<Integer>> res = new ArrayList();public List<List<Integer>> allPathsSourceTarget(int[][] graph) {List<Integer> path = new ArrayList();traverse(graph,0,path);return res;}public void traverse(int[][] graph,int s,List<Integer> path){path.add(s);int n = graph.length;if(s == n-1){res.add(new ArrayList(path));}for(int i:graph[s]){traverse(graph,i,path);}path.removeLast();}
}

2.2 课程表（环检测算法）

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

2.2.1 环检测算法 DFS版

看到依赖问题，首先想到的就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循环依赖。
具体来说，我们首先可以把课程看成「有向图」中的节点，节点编号分别是 0, 1, …, numCourses-1，把课程之间的依赖关系看做节点之间的有向边。
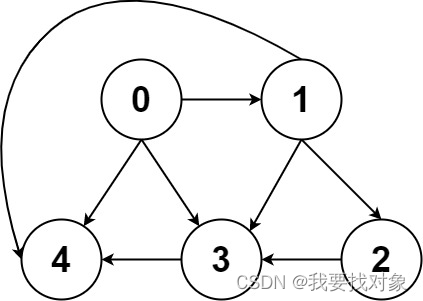
比如说必须修完课程 1 才能去修课程 3，那么就有一条有向边从节点 1 指向 3。
所以我们可以根据题目输入的 prerequisites 数组生成一幅类似这样的图：

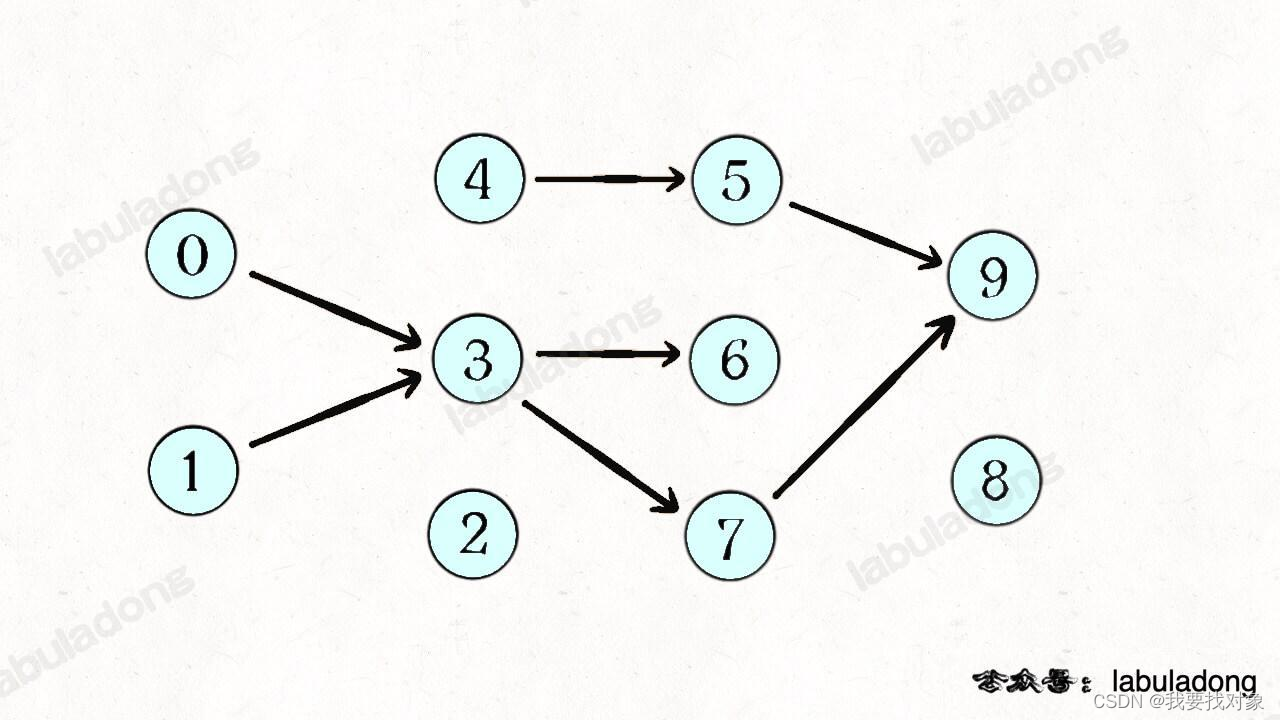
如果发现这幅有向图中存在环，那就说明课程之间存在循环依赖，肯定没办法全部上完；反之，如果没有环，那么肯定能上完全部课程。
好，那么想解决这个问题，首先我们要把题目的输入转化成一幅有向图，然后再判断图中是否存在环。
怎么转化为图？以刷题的经验，大概率是要转化为邻接表：

# graph[s] 是一个列表，存储着节点 s 所指向的节点。
List<Integer>[] graph;

首先可以写一个建图函数：

List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {// 图中共有 numCourses 个节点List<Integer>[] graph = new LinkedList[numCourses];for (int i = 0; i < numCourses; i++) {graph[i] = new LinkedList<>();}for (int[] edge : prerequisites) {int from = edge[1], to = edge[0];// 添加一条从 from 指向 to 的有向边// 边的方向是「被依赖」关系，即修完课程 from 才能修课程 tograph[from].add(to);}return graph;
}

图建出来了，怎么判断图中有没有环呢？
先不要急，我们先来思考如何遍历这幅图，只要会遍历，就可以判断图中是否存在环了。

// 防止重复遍历同一个节点
boolean[] visited;boolean canFinish(int numCourses, int[][] prerequisites) {List<Integer>[] graph = buildGraph(numCourses, prerequisites);visited = new boolean[numCourses];for (int i = 0; i < numCourses; i++) {traverse(graph, i);}
}void traverse(List<Integer>[] graph, int s) {// 代码见上文
}

注意图中并不是所有节点都相连，所以要用一个 for 循环将所有节点都作为起点调用一次 DFS 搜索算法。
这样，就能遍历这幅图中的所有节点了，你打印一下 visited 数组，应该全是 true。
现在可以思考如何判断这幅图中是否存在环。
你也可以把 traverse 看做在图中节点上游走的指针，只需要再添加一个布尔数组 onPath 记录当前 traverse 经过的路径：

boolean[] onPath;
boolean[] visited;boolean hasCycle = false;void traverse(List<Integer>[] graph, int s) {if (onPath[s]) {// 发现环！！！hasCycle = true;}if (visited[s] || hasCycle) {return;}// 将节点 s 标记为已遍历visited[s] = true;// 开始遍历节点 sonPath[s] = true;for (int t : graph[s]) {traverse(graph, t);}// 节点 s 遍历完成onPath[s] = false;
}

这里就有点回溯算法的味道了，在进入节点 s 的时候将 onPath[s] 标记为 true，离开时标记回 false，如果发现 onPath[s] 已经被标记，说明出现了环。

注意 visited 数组和 onPath 数组的区别，因为二叉树算是特殊的图，所以用遍历二叉树的过程来理解下这两个数组的区别：

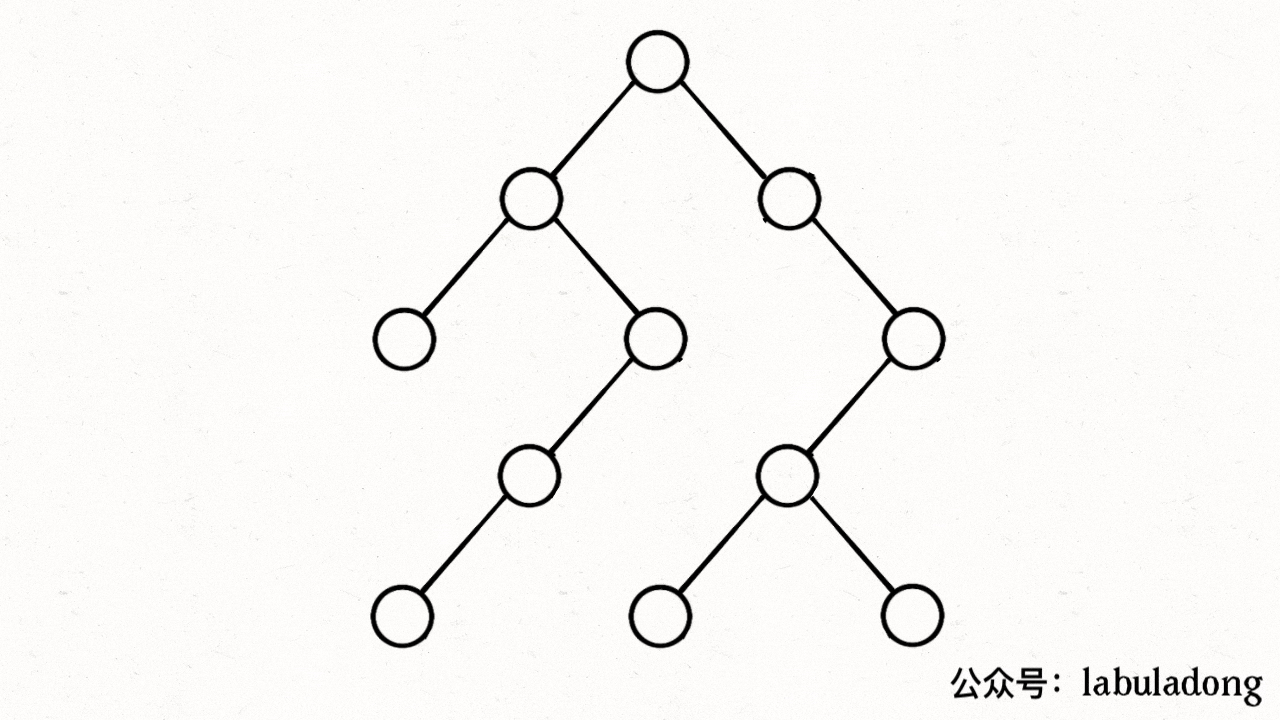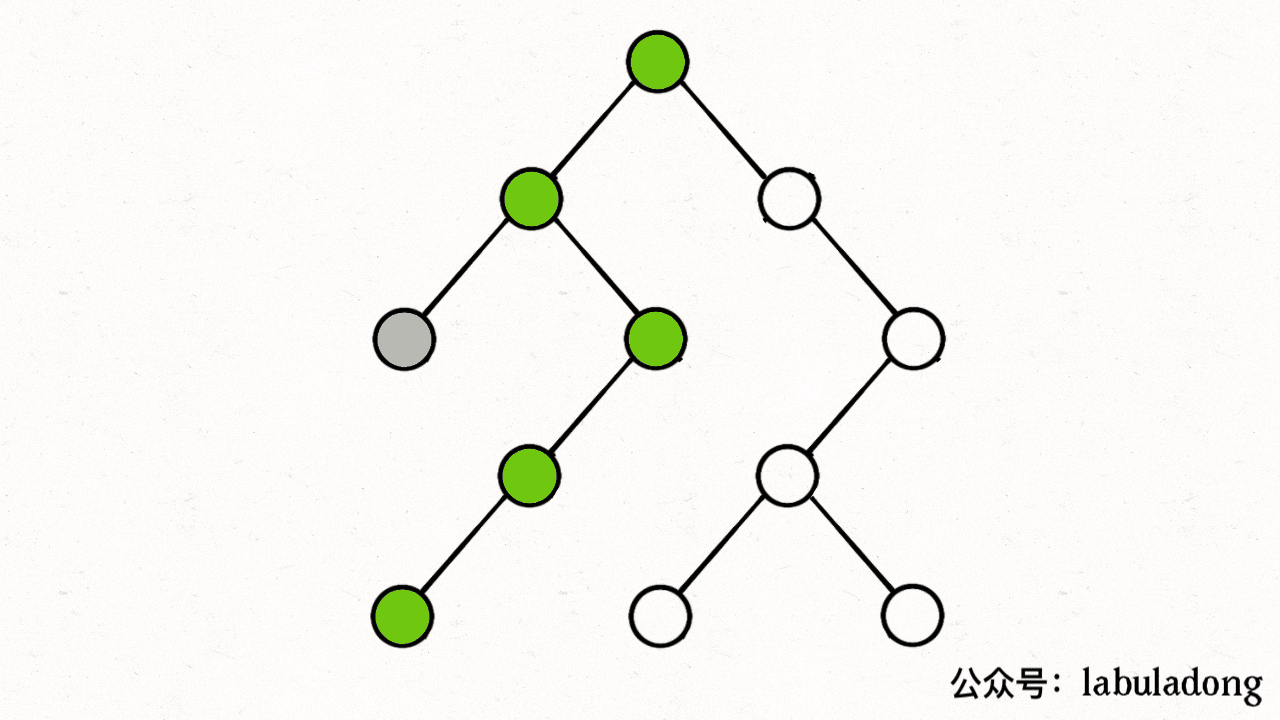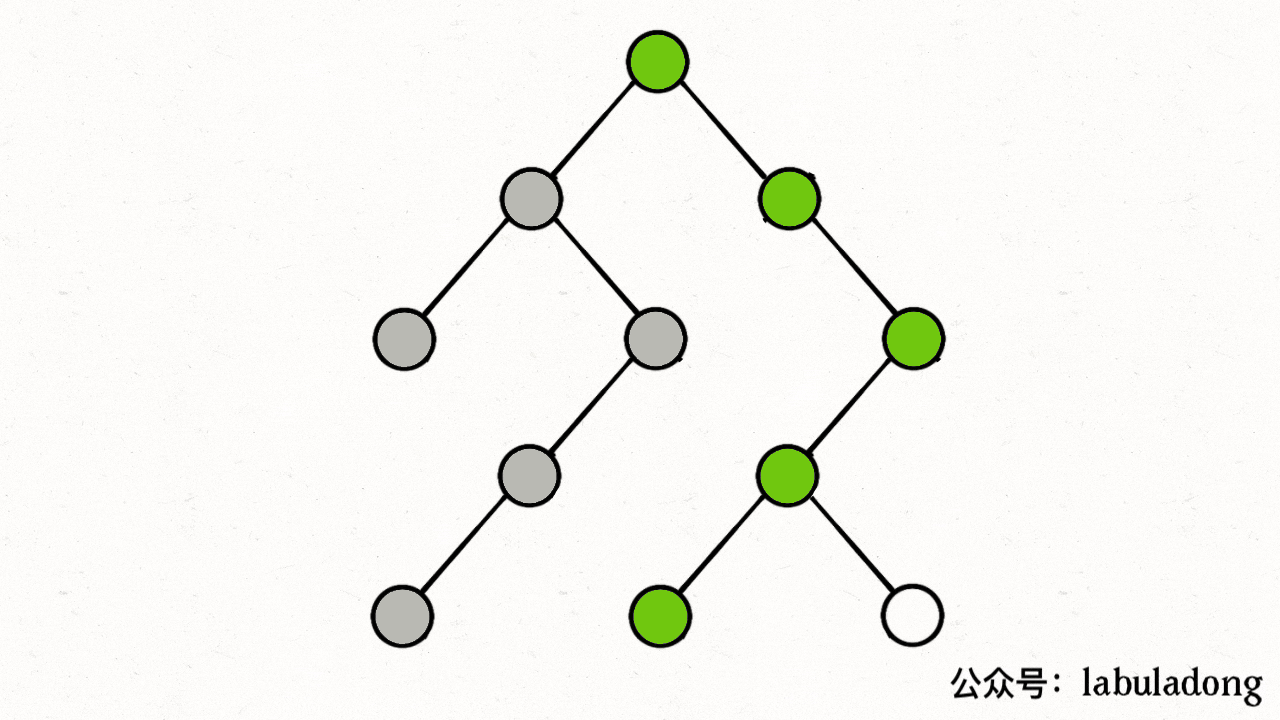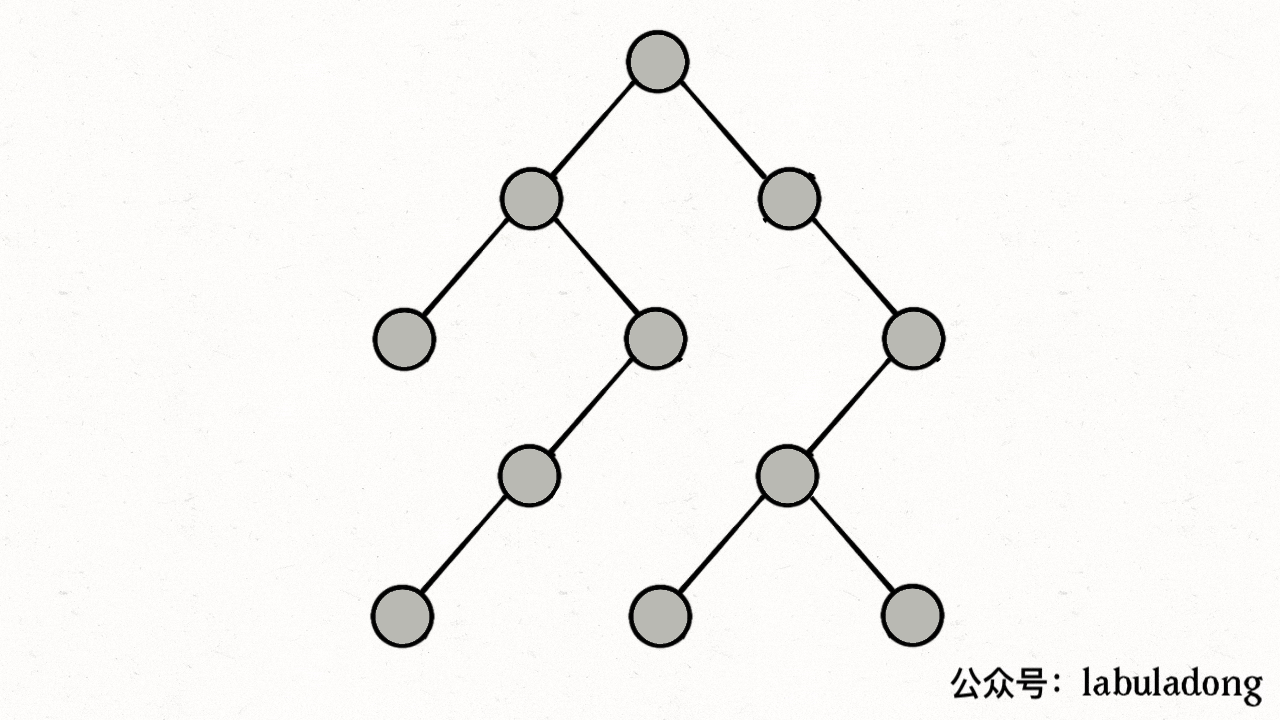
上述 GIF 描述了递归遍历二叉树的过程，在 visited 中被标记为 true 的节点用灰色表示，在 onPath 中被标记为 true 的节点用绿色表示。
因此，整理一下，完整代码如下：

class Solution {boolean[] onPath;boolean[] visited;//false表示没有环boolean result = false;public boolean canFinish(int numCourses, int[][] prerequisites) {//建图List<Integer>[] graph = buildGraph(numCourses,prerequisites);//遍历onPath = new boolean[numCourses];visited = new boolean[numCourses];for(int i = 0;i<numCourses;i++){//遍历每个结点traverse(graph,i);}return !result;}public List<Integer>[] buildGraph(int numCourses, int[][] prerequisites){List<Integer>[] graph = new ArrayList[numCourses];//图有numCourse个结点for(int i = 0;i<numCourses;i++){graph[i] = new ArrayList();}for(int[] i:prerequisites){int start = i[0];int end = i[1];graph[start].add(end);}return graph;}public void traverse(List<Integer>[] graph,int s){if(onPath[s]){result = true;}if(visited[s] || result){return;}visited[s] = true;onPath[s] = true;for(int i:graph[s]){traverse(graph,i);}onPath[s] = false;}
}

2.2.2 环检测算法 BFS版

2.3 课程表 II （拓扑排序算法）

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。
例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
示例 2：

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3：

输入：numCourses = 1, prerequisites = []
输出：[0]

2.3.1 拓扑排序 DFS版

什么是拓扑排序？
直观地说就是，让你把一幅图「拉平」，而且这个「拉平」的图里面，所有箭头方向都是一致的
很显然，如果一幅有向图中存在环，是无法进行拓扑排序的，因为肯定做不到所有箭头方向一致；反过来，如果一幅图是「有向无环图」，那么一定可以进行拓扑排序。
其实也不难看出来，如果把课程抽象成节点，课程之间的依赖关系抽象成有向边，那么这幅图的拓扑排序结果就是上课顺序。
首先，我们先判断一下题目输入的课程依赖是否成环，成环的话是无法进行拓扑排序的，所以我们可以复用上一道题的主函数：

public int[] findOrder(int numCourses, int[][] prerequisites) {if (!canFinish(numCourses, prerequisites)) {// 不可能完成所有课程return new int[]{};}// ...
}

那么关键问题来了，如何进行拓扑排序？是不是又要秀什么高大上的技巧了？
其实特别简单，将后序遍历的结果进行反转，就是拓扑排序的结果。
直接上代码：

class Solution {boolean[] onPath;boolean[] visited;boolean hasCycle = false;// 记录后序遍历结果List<Integer> postorder = new ArrayList<>();public int[] findOrder(int numCourses, int[][] prerequisites) {List<Integer>[] graph = buildgrap(numCourses,prerequisites);onPath = new boolean[numCourses];visited = new boolean[numCourses];for(int i = 0;i<numCourses;i++){traverse(graph,i);}if(hasCycle){return new int[]{};}Collections.reverse(postorder);int[] res = new int[numCourses];for(int i = 0;i<numCourses;i++){res[i] = postorder.get(i);}return res;}public List<Integer>[] buildgrap(int numCourses,int[][] prerequisites){List<Integer>[] graph = new ArrayList[numCourses];for(int i = 0;i<numCourses;i++){graph[i] = new ArrayList();}for(int[] i:prerequisites){int start = i[1];int end = i[0];graph[start].add(end);}return graph;}public void traverse(List<Integer>[] graph,int s){if(onPath[s]){hasCycle = true;}if(hasCycle || visited[s]){return;}onPath[s] = true;visited[s] = true;for(int i:graph[s]){traverse(graph,i);}onPath[s] = false;postorder.add(s);}
}