1.代码速览
class Solution2
{
public:string addStrings(string num1, string num2){//end1和end1是下标int end1 = num1.size() - 1;int end2 = num2.size() - 1;string str;//下标(指针)从后向前走,走到头才可以结束,所以是end>=0int next = 0;while (end1 >= 0 || end2 >= 0){int x1 = end1 >= 0 ? num1[end1--] - '0' : 0;//'0' = 48int x2 = end2 >= 0 ? num2[end2--] - '0' : 0;int x = x1 + x2 + next;//18 10next = x / 10;//18/10 = 1 进位 1x = x % 10;//18%10 = 8 本位 0//头插//str.insert(0, 1, x + '0');//将数子恢复成字符str += (x + '0');}if (next == 1)//处理头是9+1的情况{/*str.insert(str.begin(), '1');*/str += '1';}reverse(str.begin(), str.end());return str;}
};2.代码详解

我举一个较为极端的例子来说明此代码的运行逻辑,这个例子也可更全面的概括了几乎所有的情况
"99"+'9':
2.1逐步骤分析
a.以竖式计算的逻辑,绝对是从个位开始相加,即'9'+'9',于是,我们便要想办法定位到这个位子,
于是我们便设置下标end1和end2来定位这两个字符串的最后一位(个位)

在C++的STL中,我们一般使用size()来计算当前容器中字符串的大小,num1.size()-1可以得出下标;
b.因为9+9=18,在竖式计算中,这里的18是需要留8进1的,于是我们便声明一个变量next来储存这个进位,并且将next初始化为0
结合手绘图,我们可以得出结论,在进行竖式计算的过程中,一个数字的得出其实由三个部分的相加组成,是x1+x2+next
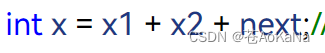
c.这两个数字字符串的相加可以,首元素的下标为0,当end1和end2>=0时此循环才可以进行,在进行加法计算的过程中结果的x=x1+x2+next;x1和x2便是下标end1和end2目前所指向的数字,在end1和end2遍历完字符串中所有数字符字后循环方可停止![]()
d.用end1和end2对两个字符串进行遍历

如果这个位置有字符,就将这个字符显示类型转换成int类型的数字
在c语言和C++中,字符实际上是以整数形式存储的,它们的值是它们对应的 ASCII 值,证明过程如下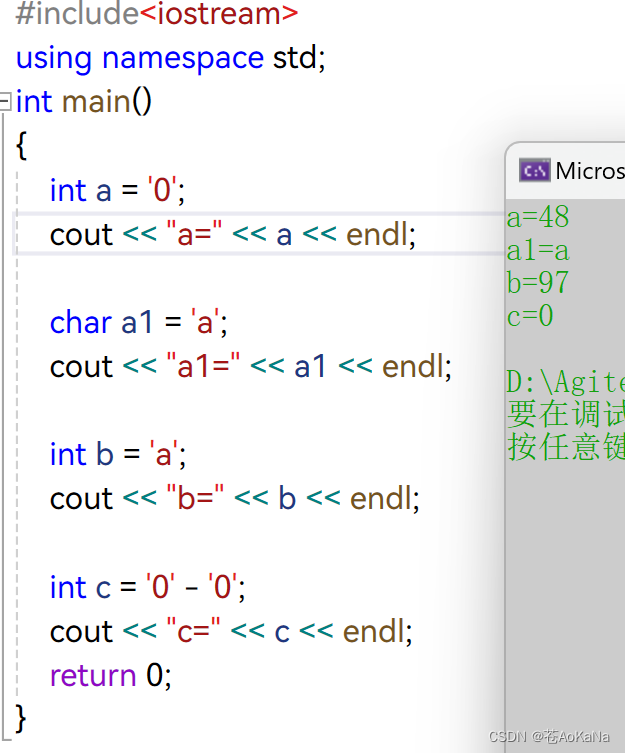
所以这里使用显式类型转换和字符串(ASCII)相减得出int的整数(就是由字符数字转换成int型的数字)
e.在考虑好将单个位置上的数字相加工作做完以后我们便可以考虑进位数字的求得和本位数字的保留问题了

f.在将它的每个位置取下后将需要保留的位置依次放入字符串中形成新的数字,有两种方法,可以尾插然后使用reverse()倒一下,或者直接头插

这里建议尾插,如果头插那么时间复杂度将会是O(N²),如果尾插后reverse便是O(N);






![[基础] Unity Shader:顶点着色器(vert)函数](https://img-blog.csdnimg.cn/direct/7a37aa91bbdd4ba78d23fe22cc4b6d4c.gif)
![[C++][数据结构]二叉搜索树:介绍和实现](https://img-blog.csdnimg.cn/direct/6f3eecc7fa6f472db3e13b17244bffa3.png)