算法-并查集

什么是并查集

并查集基础

（1）原理

（2）初始化

（3）查询

（4）合并

（5）判断是否同一集合

并查集优化

路径压缩

启发式合并

并查集模板

模板

例题

带权并查集

例题

分析

Code

什么是并查集

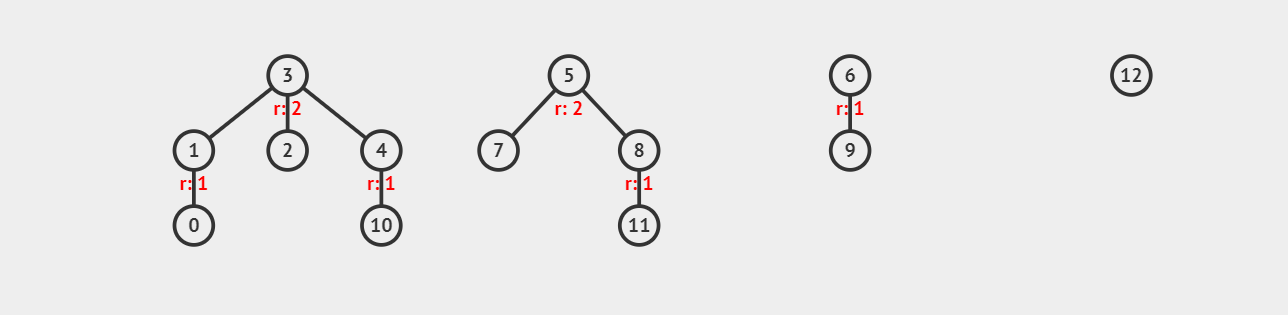
并查集是一种树形的数据结构，我们可以使用它来进行集合上的合并与查询等问题。具体来说，它支持两种操作：

合并：将两个集合合并成一个集合。
查询：确定某个元素处于哪个集合。

如图，{3,1,2,4,0,10}{3,1,2,4,0,10} 表示一个集合，{5,7,8,11}{5,7,8,11} 表示另一组集合。

可以看出并查集是多叉树结构，我们用根节点来表示这个根节点所在的集合(即根节点作为集合的"代表元素")。

并查集基础

（1）原理

从代码层面，我们如何将两个元素添加到同一个集合中呢？

我们将三个元素A，B，C （分别是数字）放在同一个集合，其实就是将三个元素连通在一起，如何连通呢。

只需要用一个一维数组来表示，即：father[A] = B，father[B] = C 这样就表述 A 与 B 与 C连通了（有向连通图）。代码如下：

// 将v，u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回p[v] = u;
}

这样我们就可以知道 A 连通 B，因为 A 是索引下标，根据 father[A]的数值就知道 A 连通 B。那怎么知道 B 连通 A呢？

如果我们的目的是判断这三个元素是否在同一个集合里，知道 A 连通 B 就已经足够了。这里要讲到寻根思路，只要 A ，B，C 在同一个根下就是同一个集合。

给出A元素，就可以通过 father[A] = B，father[B] = C，找到根为 C。给出B元素，就可以通过 father[B] = C，找到根也为为 C，说明 A 和 B 是在同一个集合里。大家会想第一段代码里find函数是如何实现的呢？其实就是通过数组下标找到数组元素，一层一层寻根过程，代码如下：

// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u; // 如果根就是自己，直接返回else return find(father[u]); // 如果根不是自己，就根据数组下标一层一层向下找
}

（2）初始化

在我们初始创建数据的时候，由于没有任何操作，所以每个元素都是一个独立的集合，显然，每个元素都是本身集合的根节点。

// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {p[i] = i;}
}

（3）查询

假设我们现在要查询元素 0 的父节点，该怎么做呢？

很简单，由于根节点的父节点就是本身（不知道的可以回顾一下初始化过程）。所以我们直接检查 0 的父节点是否为 0 即可。

如果 0 父节点为 0 ，说明 0 是所属集合的根节点，返回 0 即可。（因为我们用根节点代表集合）
如果 0 父节点不为 0 ，那么我们只需要递归检查它的父节点是否为 0 即可。

我们发现 0 的父节点是 2 ，那么我们继续检查 2 是否为根节点 (p[2] == 2) ，不是，则继续检查 3 ，此时 3 为根节点，于是返回 3 。

查询的复杂度为被查询元素在树上的深度。

int find(int u){return p[x] == x ? x : find(p[x]);
}

（4）合并

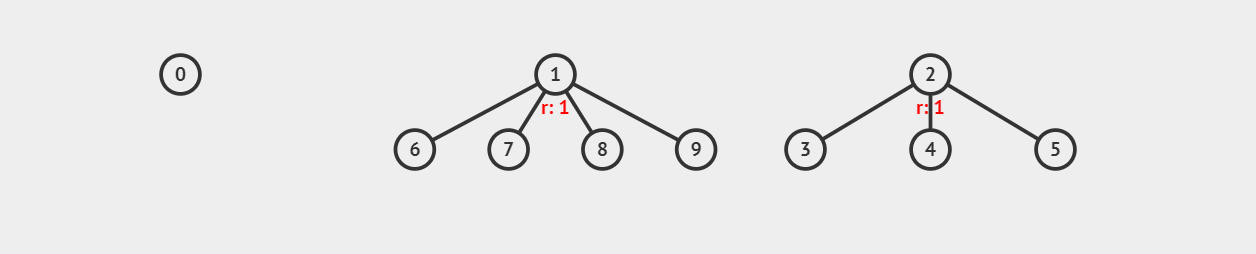
如图，如何合并 6 所属集合和 3 所属集合？由于我们知道根节点代表整个集合，合并 6 和 3 即意味着它们合并后根节点相同，我们可以任意取一个子集的根节点作为合并后的根节点，比如取 3 后：

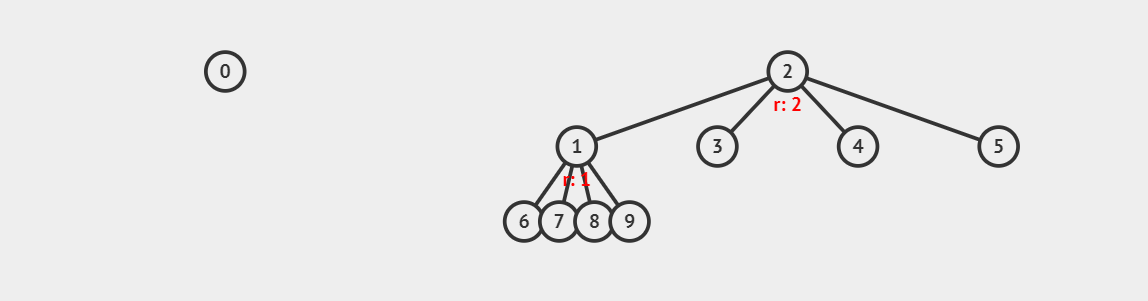
我们选择了把 2 作为合并后集合的根节点（代表元素）。

void merge (int u, int v) {u = find(u);v = find(v); // x 和 y 为根节点p[u] = v; // 直接把其中一个集合合并到另外一个集合
}

（5）判断是否同一集合

最后我们如何判断两个元素是否在同一个集合里，如果通过 find函数找到两个元素属于同一个根的话，那么这两个元素就是同一个集合。

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}

并查集优化

路径压缩

我们发现，由于每次查询某个元素需要查询 𝑟 次(𝑟 为当前元素在树上的深度)，当树的深度很大，且我们要查询的元素在很深的地方，那么查询所需要耗费的时间就很大，有没有办法优化呢？

答案是肯定的，我们发现，整个集合只有代表元素是'有用'的，其他元素仅能代表它在这个集合中，与它所处的位置没有关系。 于是，我们在每次查询后，就把当前元素的父节点设置为集合的根节点，根节点就是 𝑓𝑖𝑛𝑑 的返回值，所以：

int find (int x) // find 函数返回x所属集合代表元素
{return p[x] == x ? x : p[x] = find(p[x]); // 把x的父节点设置为根节点
}

启发式合并

上述提到，树的深度会影响查询的速度，那么我们可以在合并的时候，把集合元素较少的合并到集合元素较大的即可。还可以按照集合树的深度与集合的元素数量评估来得到更好的合并方法。

void merge(int u, int v) // 按秩合并需要用到集合内的数量
{u = find(u); // 找到节点 u 的根v = find(v); // 找到节点 v 的根if (size[u] > size[v]) {swap(u, v); // 如果节点 u 所在集合的大小大于节点 v 所在集合的大小，则交换它们}size[v] += size[u]; // 更新节点 v 所在集合的大小p[u] = v; // 将节点 u 所在集合的根连接到节点 v 所在集合的根上
}

并查集模板

模板

const int N = 200010;int p[N]; // p[i] 表示节点 i 的父节点// 将节点 v 和节点 u 连接到同一个集合
void join(int u, int v) {u = find(u); // 寻找节点 u 的根v = find(v); // 寻找节点 v 的根if (u == v) return; // 如果节点 u 和节点 v 已经在同一个集合中，则不需要连接，直接返回p[v] = u; // 将节点 v 的根连接到节点 u 的根上
}// 初始化并查集
void init(int n) {for (int i = 0; i < n; i++) {p[i] = i; // 初始化每个节点的父节点为自身}
}// 查找节点 u 的根，并进行路径压缩
int find(int u) {return p[u] == u ? u : p[u] = find(p[u]); // 如果节点 u 的父节点不是自身，则递归查找其父节点，并进行路径压缩
}// 将节点 u 和节点 v 所在的集合合并
void merge(int u, int v) {u = find(u); // 寻找节点 u 的根v = find(v); // 寻找节点 v 的根p[v] = u; // 将节点 v 的根连接到节点 u 的根上
}// 判断节点 u 和节点 v 是否属于同一个集合
bool isSame(int u, int v) {u = find(u); // 寻找节点 u 的根v = find(v); // 寻找节点 v 的根return u == v; // 如果节点 u 和节点 v 的根相同，则它们属于同一个集合，返回 true，否则返回 false
}

例题

684. 冗余连接 - 力扣（LeetCode）

int n = 1005;// 并查集初始化
void init(int* father) {for (int i = 0; i < n; ++i) {father[i] = i;}
}// 并查集里寻根的过程
int find(int u, int* father) { return u == father[u] ? u : (father[u] = find(father[u], father)); 
}// 判断 u 和 v 是否找到同一个根
bool isSame(int u, int v, int* father) {u = find(u, father);v = find(v, father);return u == v;
}// 将 v->u 这条边加入并查集
void join(int u, int v, int* father) {int rootU = find(u, father); // 寻找u的根int rootV = find(v, father); // 寻找v的根if (rootU == rootV) {return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回}father[rootV] = rootU;
}int* findRedundantConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize) {int father[n];init(father);for (int i = 0; i < edgesSize; i++) {if (isSame(edges[i][0], edges[i][1], father)) {*returnSize = 2;return edges[i];} else {join(edges[i][0], edges[i][1], father);}}*returnSize = 0;return NULL;
}

带权并查集

当然，维护了数量在某些情况也是不够用的，我们还需要知道集合内各个元素的关系。我们可以使用带权并查集，使用边权来维护当前元素与父节点的某种关系。即，带权并查集可以维护元素之间的制约关系。我们以一道经典例题为例。

例题

动物王国中有三类动物 A, B, C，这三类动物的食物链构成了有趣的环形。

A 吃 B，B 吃 C，C 吃 A。

现有 N 个动物，以 1∼N 编号。

每个动物都是 A, B, C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X 和 Y 是同类。

第二种说法是 2 X Y，表示 X 吃 Y。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 X 或 Y 比 N 大，就是假话；
当前的话表示 X 吃 X，就是假话。

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

分析

给出两个动物，它们有吃、被吃以及同类三种制约关系，而带权并查集可以很好地维护元素间的制约关系。

设 d[x] 表示元素 x 与其父节点的边的边权，规定：

d[x] % 3 = 0 表示 x 与父节点 p[x] 是同类。
d[x] % 3 = 1 表示 x 可以吃父节点 p[x]。
d[x] % 3 = 2 表示 x 可以被父节点 p[x] 吃。
那么我们判定假话，只需要不满足 d[x] 即可。

简单来说：

判断 x 与 y 为同类，但已经制约了 x 和 y 为异类（吃或被吃）。
判断 x 吃 y ，但已经制约了 x 和 y 是同类或者 x 被 y 吃。
判断 x 被 y 吃，但已经制约了 x 和 y 是同类或者 x 被 y 吃。（题目不会给定）

首先我们肯定要是有路径压缩来优化查询的，在路径压缩后， x 对应的父节点变为集合根节点，因此 d[x] 也需要做变换。

int find (int x)
{if (x != p[x]){int u = find(p[x]);/** 注意此时x还没有路径优化，父节点仍然保持原来的父节点* 此时 x 以上的节点经过路径优化，d[p[x]] 也修改为正确值(x父节点与根节点的关系)* 那么我们只需要根据x与父节点的关系、x父节点与根节点的关系即可传递得到x与根节点的关系，再路径优化即可。*/d[x] += d[p[x]];p[x] = u;}return p[x];
}

那么现在的问题就是，如何知道一个集合里两个元素的制约关系？

由于我们求得 ( d[x] ) 都是 ( x ) 与根节点的关系，那么 ( (d[x] - d[y]) % 3 ) 即为 ( x ) 与 ( y ) 的制约关系。

如何合并两个关系呢？

假设判定 ( x ) 和 ( y ) 的关系的边权表示为 ( op )，由于在 find 中我们可以求得 ( x ) 、( y ) 分别与其根节点的关系，且现在 ( x ) 与 ( y ) 的制约关系也知道了，那么根据传递性我们也可以求出两个集合根节点之间的制约关系，合并两个集合时维护好两个根节点的制约关系即可。

假设 ( x ) 的根节点为 ( p_x )， ( y ) 的根节点为 ( p_y )。现在要把 ( p_x ) 合并到 ( p_y )。

1.判定 ( x ) 与 ( y ) 同类

        在合并后的集合里， ( x ) 与 ( y ) 的关系应该为 ( (d[x] - d[y]) % 3 = 0 )。由于此时的 ( d[x] ) 是合并后的，所以合并前应该为 ( d[x] + d[p_x] )。即 ( d[x] + d[p_x] - d[y] = 0 )，那么 ( d[p_x] = d[y] - d[x] )。

2.判定 ( x ) 与 ( y ) 不同类

        由于题目给定此时判定为 ( x ) 吃 ( y )，所以我们只需要考虑这一种。

        在合并后的集合里， ( x ) 与 ( y ) 的关系应该是： ( d[x] - d[y] = 1 )，即 ( x ) 可以吃根节点（路径压缩后的父节点），且根节点与 ( y ) 同类，依次推类。

        同样此时的 ( d[x] ) 是合并后的，合并前应该是 ( d[x] + d[p_x] )，所以 ( d[x] + d[p_x] - d[y] = 1 )，即 ( d[p_x] = 1 + d[y] - d[x] )。

Code

#include <stdio.h>const int N = 50010;int n, m;
int p[N], d[N];int find(int x) {if (p[x] != x) {int t = find(p[x]);d[x] += d[p[x]];p[x] = t;}return p[x];
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {p[i] = i;d[i] = 0;  // 将距离模3数组初始化为0}int res = 0;while (m--) {int t, x, y;scanf("%d%d%d", &t, &x, &y);if (x > n || y > n) {res++; // 谎言类型1：动物编号超出限制} else {int px = find(x), py = find(y);if (t == 1) {if (px == py && (d[x] - d[y]) % 3 != 0) res++; // 谎言类型2：声称相同种类但约束条件不成立else if (px != py) {p[px] = py;d[px] = (d[y] - d[x] + 3) % 3;  // 确保结果非负}}else {if (px == py && (d[x] - d[y] - 1) % 3 != 0) res++; // 谎言类型3：声称x吃y但约束条件不成立else if (px != py) {p[px] = py;d[px] = (d[y] + 1 - d[x] + 3) % 3; // 确保结果非负}}}}printf("%d\n", res);return 0;
}