今天我们学习一种算法：排序算法（本文的排序默认是从小到大顺序）！！！

1、直接插入排序

算法原理： 每次将无序序列中的第一个插入到有序序列当中，使有序序列仍为有序，第一趟排序默认第一个元素是有序的，类比于生活中的摸牌，每次将新的排插入已有的牌当中。直接插入排序的算法原理很简单，我们只需要找到每个元素该插入到哪个位置即可。

代码实现：

    public void InsertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {array[j + 1] = tmp;break;}}array[j + 1] = tmp;}}

代码图解：

2、希尔排序

算法原理： 希尔排序又称缩小增量排序，原理是先选定一个数作为分组的组数，将数组进行分组，接着分别对每个组进行排序，每组排序好之后，缩小分组的组数，重复上述步骤，直到组数为1。对每个组进行排序，我们使用插入排序的方法进行排序。

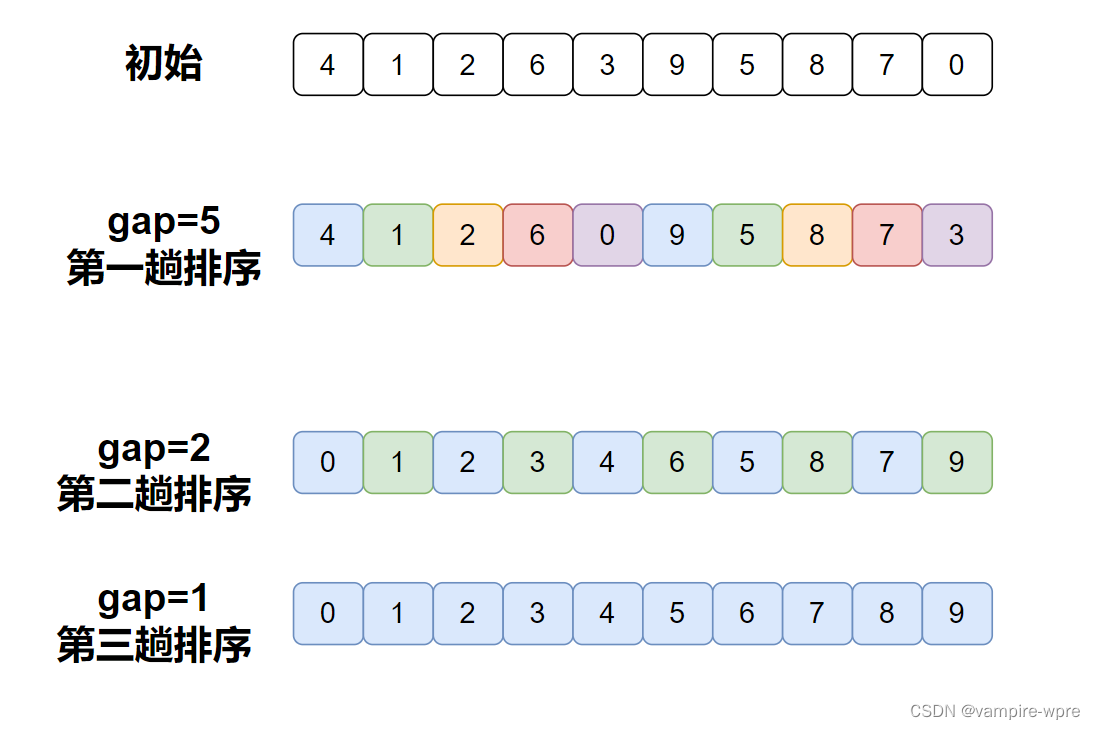
代码实现：

    public void ShellSort(int[] array) {int gap = array.length;//分成gap组,对每一组进行插入排序while (gap > 1) {gap /= 2;shell(array, gap);}}//对每组进行插入排序public void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {array[j + gap] = tmp;break;}}array[j + gap] = tmp;}}

3、直接选择排序

算法原理： 每次待排序序列中选择最小的元素和待排序的第一个元素交换
代码实现：

    public void SelectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}//交换minIndex下标和i下标的值int tmp = array[minIndex];array[minIndex] = array[i];array[i] = tmp;}}

4、堆排序

算法原理： 堆排序是借用堆这种数据结构来实现的一种排序算法，如果升排序，建立大根堆；如果排降序，建立小根堆 。建堆之后：
1、交换0下标元素和最后一个元素的值
2、然后重新将数组进行向下调整为大根堆
重复这两个步骤，直到全部有序

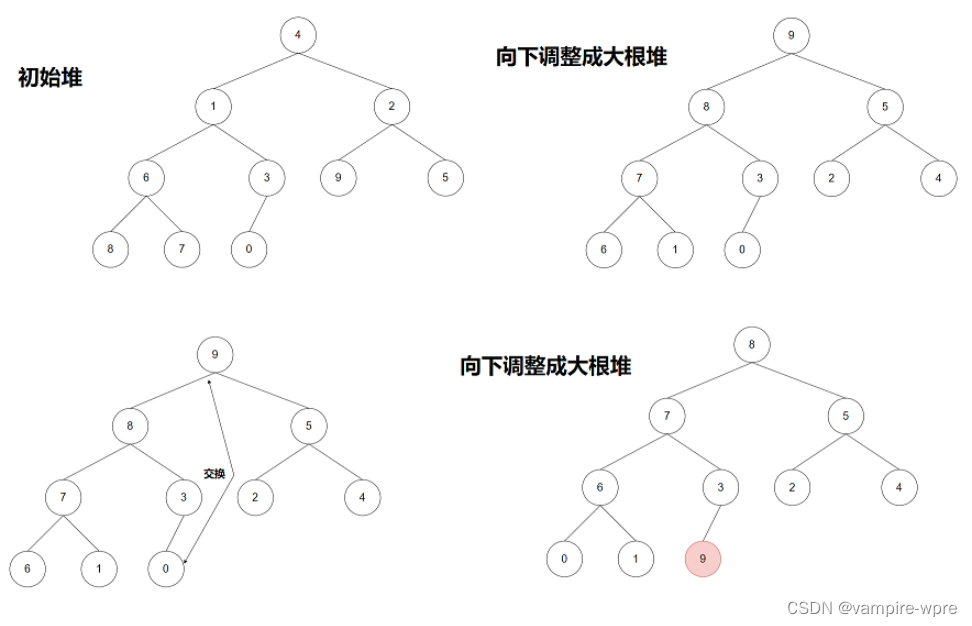
代码实现：

    public void HeapSort(int[] array) {//先创建大堆createBigHeap(array);int end = array.length - 1;while (end >= 0) {//交换int tmp = array[0];array[0] = array[end];array[end] = tmp;ShiftDown(array, 0, end);end--;}}public void createBigHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {ShiftDown(array, parent, array.length);}}public void ShiftDown(int[] array, int parent, int end) {int child = parent * 2 + 1;while (child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {//交换int tmp = array[parent];array[parent] = array[child];array[child] = tmp;parent = child;child = parent * 2 + 1;} else {break;}}}    

5、冒泡排序

算法原理： 遍历数组，每次比较相邻两个元素的大小，如果大的数字在前则交换两个元素的位置，这样就完成了一趟冒泡排序，此时最大的数到了最后，然后对前n-1个数进行相同的操作，直到有序。
代码实现：

    public void BubbleSort(int[] array) {for (int i = 0; i < array.length-1; i++) {for (int j = i; j < array.length - i - 1; j++) {if (array[j] > array[j + 1]) {//交换int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;}}}}

问题：如果遍历一遍数组已经有序了，就不用再继续比较下去了，因此对上面代码进行优化
优化后:

    public void BubbleSort(int[] array) {boolean flg = false;for (int i = 0; i < array.length - 1; i++) {for (int j = i; j < array.length - i - 1; j++) {if (array[j] > array[j + 1]) {//交换int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;flg = true;}}if (!flg) {break;}}}

6、快速排序

算法原理： 快速排序的基本思想就是：选定一个基准，通过一趟快速排序之后，能把数据分割为两部分，左边部分比基准的值小，右边的部分比基准的值大，接着再按照这个方法分别对基准左边部分和右边部分进行递归，重复这个步骤直到整个序列都有序。快速排序的最重要部分就是如何将序列分割成两部分，常见的分割方法有hoare法和挖坑法
Hoare法分割： 先选定一个基准（默认是第一个元素），定义left、right下标，left从序列最右边开始找比基准小的值（升序排序），找到之后停下来，接着让left从最左边开始找比基准大的值，找到之后停下来，将找到的这两个值交换，当left和right相遇时(left=right)，交换基准的值和left/right下标的值，这样left/right下标左边的元素全都比left/right下标的值小,右边的元素都比它大，这样就分割好了。
图解：

挖坑法：
和Hoare法的区别是：挖坑法是边找边交换，如图

6.1 递归实现

代码实现：

    public void QuickSort(int[] arr) {quick(arr, 0, arr.length - 1);}public void quick(int[] arr, int left, int right) {//递归结束的条件if (left >= right) {return;}//进行分割int pio = partition(arr, left, right);quick(arr, 0, pio - 1);quick(arr, pio + 1, right);}

hoare法分割

    public int partition(int[] arr, int left, int right) {int tmp = arr[left];int i = left;while (left < right) {while (left < right && arr[right] >= tmp) {right--;}while (left < right && arr[left] <= tmp) {left++;}//交换int tmp = array[right];array[right] = array[left];array[left] = tmp;}//交换int tmp = array[i];array[i] = array[left];array[left] = tmp;return left;}

挖坑法分割

    public int partition(int[] arr, int left, int right) {int tmp = arr[left];while (left < right) {while (left < right && arr[right] >= tmp) {right--;}arr[left] = arr[right];while (left < right && arr[left] <= tmp) {left++;}array[right] = array[left];}arr[left] = tmp;return left;}

优化： 如果待排序序列是：1、2、3、4、5这种有序的序列，假如还是取第一个元素为基准，就会出现左边没有小于基准的值，如何让每次分割都是均匀分割？方法很简单，取序列最左边、最右边和中间位置的三个元素的中位数作为基准，再进行Hoare法或者挖坑法分割，此时每次都能均匀分割，如图

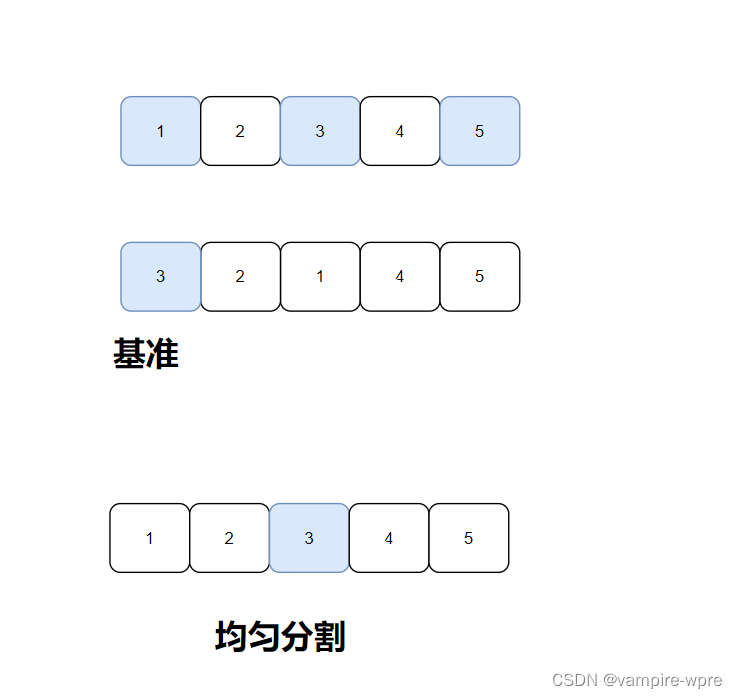
优化后：

    public void QuickSort(int[] arr) {quick(arr, 0, arr.length - 1);}public void quick(int[] arr, int left, int right) {//递归if (left >= right) {return;}//中位数的值作为基准int midIndex = midThreeIndex(arr, left, right);//交换int tmp = arr[left];arr[left] = arr[midIndex];arr[midIndex] = tmp;    int pio = partition(arr, left, right);quick(arr, 0, pio - 1);quick(arr, pio + 1, right);}public int partition(int[] arr, int left, int right) {int tmp = arr[left];int i = left;while (left < right) {while (left < right && arr[right] >= tmp) {right--;}while (left < right && arr[left] <= tmp) {left++;}swap(arr, right, left);}swap(arr, i, left);return left;}        

6.2 非递归实现

原理： 利用栈这个数据结构来实现。首先先对序列进行一次分割（Hoare法或者挖坑法都可以），将基准左边部分的left、right下标入栈，再将右边部分的left、right下标入栈，然后出栈两个元素作为新的left、right来进行分割，重复上述步骤，直到栈为空

代码实现：

    public void QuickSortNoRecursion(int[] arr) {Stack<Integer> stack = new Stack<>();int left = 0;int right = arr.length - 1;int pio = partition(arr, left, right);if (pio > left + 1) {stack.push(left);stack.push(pio - 1);}if (pio < right - 1) {stack.push(pio + 1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pio = partition(arr, left, right);if (pio > left + 1) {stack.push(left);stack.push(pio - 1);}if (pio < right - 1) {stack.push(pio + 1);stack.push(right);}}}

7、归并排序

原理： 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；归并排序的思想是：先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

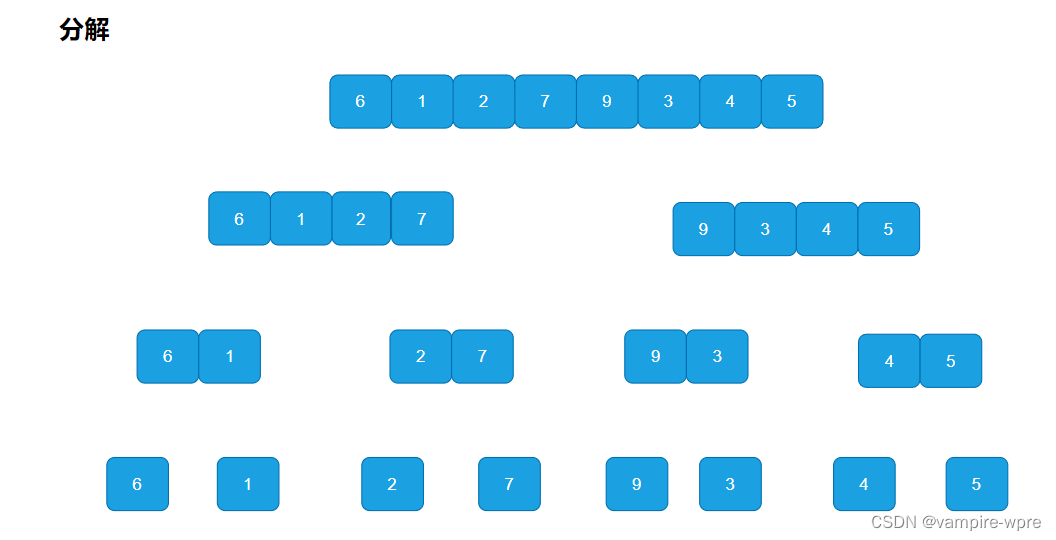
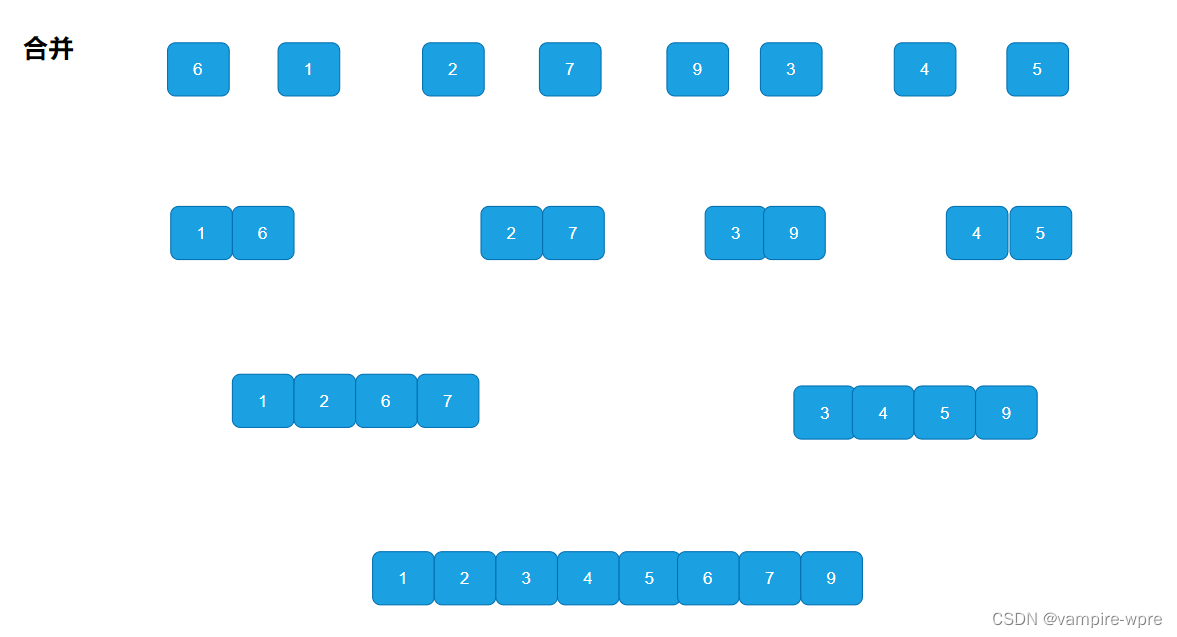
7.1 递归实现

递归思路： 先将序列进行分解，直到分解为单个元素为一组，然后再进行合并。合并：开辟新的数组，新的数组存储的是合并之后且有序的子序列，再开辟的新数组的元素拷贝回原数组

    public void mergeSort(int[] arr) {merge(arr, 0, arr.length - 1);}public void merge(int[] arr, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;//分解merge(arr, left, mid);merge(arr, mid + 1, right);//合并mergeFun(arr, left, mid, right);}//合并public void mergeFun(int[] arr, int left,int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int k = 0;int[] tmp = new int[right - left + 1];//开辟新的数组while (s1 <= e1 && s2 <= e2) {if (arr[s1] < arr[s2]) {tmp[k++] = arr[s1++];} else {tmp[k++] = arr[s2++];}}while (s1 <= e1) {tmp[k++] = arr[s1++];}while (s2 <= e2) {tmp[k++] = arr[s2++];}//此时tmp有序了,拷回到原数组for (int i = 0; i < k; i++) {arr[left + i] = tmp[i];}}

7.2 非递归实现

非递归省去了分解的步骤，直接对数组进行合并

    //非递归public void mergeSortN(int[] arr) {mergeN(arr);}//没有分解的过程private void mergeN(int[] arr) {int gap = 1;while (gap <= arr.length) {for (int i = 0; i < arr.length; i = i + 2 * gap) {int mid = i + gap - 1;if (mid >= arr.length) {mid = arr.length - 1;}int right = mid + gap;if (right >= arr.length) {right = arr.length - 1;}mergeFun(arr, i, mid, right);}gap *= 2;}}public void mergeFun(int[] arr, int left,int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int k = 0;int[] tmp = new int[right - left + 1];while (s1 <= e1 && s2 <= e2) {if (arr[s1] < arr[s2]) {tmp[k++] = arr[s1++];} else {tmp[k++] = arr[s2++];}}while (s1 <= e1) {tmp[k++] = arr[s1++];}while (s2 <= e2) {tmp[k++] = arr[s2++];}//此时tmp有序了,拷回到原数组for (int i = 0; i < k; i++) {arr[left + i] = tmp[i];}}

8、性能分析

性能包括：时间复杂度、空间复杂度、稳定性

排序算法	平均时间复杂度	空间复杂度	稳定性
插入排序	O(n^2)	O(1)	稳定
希尔排序	O(和增量有关)	O(1)	不稳定
选择排序	O(n^2)	O(1)	不稳定
堆排序	O(n*logn)	O(1)	不稳定
冒泡排序	O(n^2)	O(1)	稳定
快速排序	O(n*logn)	O(logn)	不稳定
归并排序	O(n*logn)	O(n)	稳定