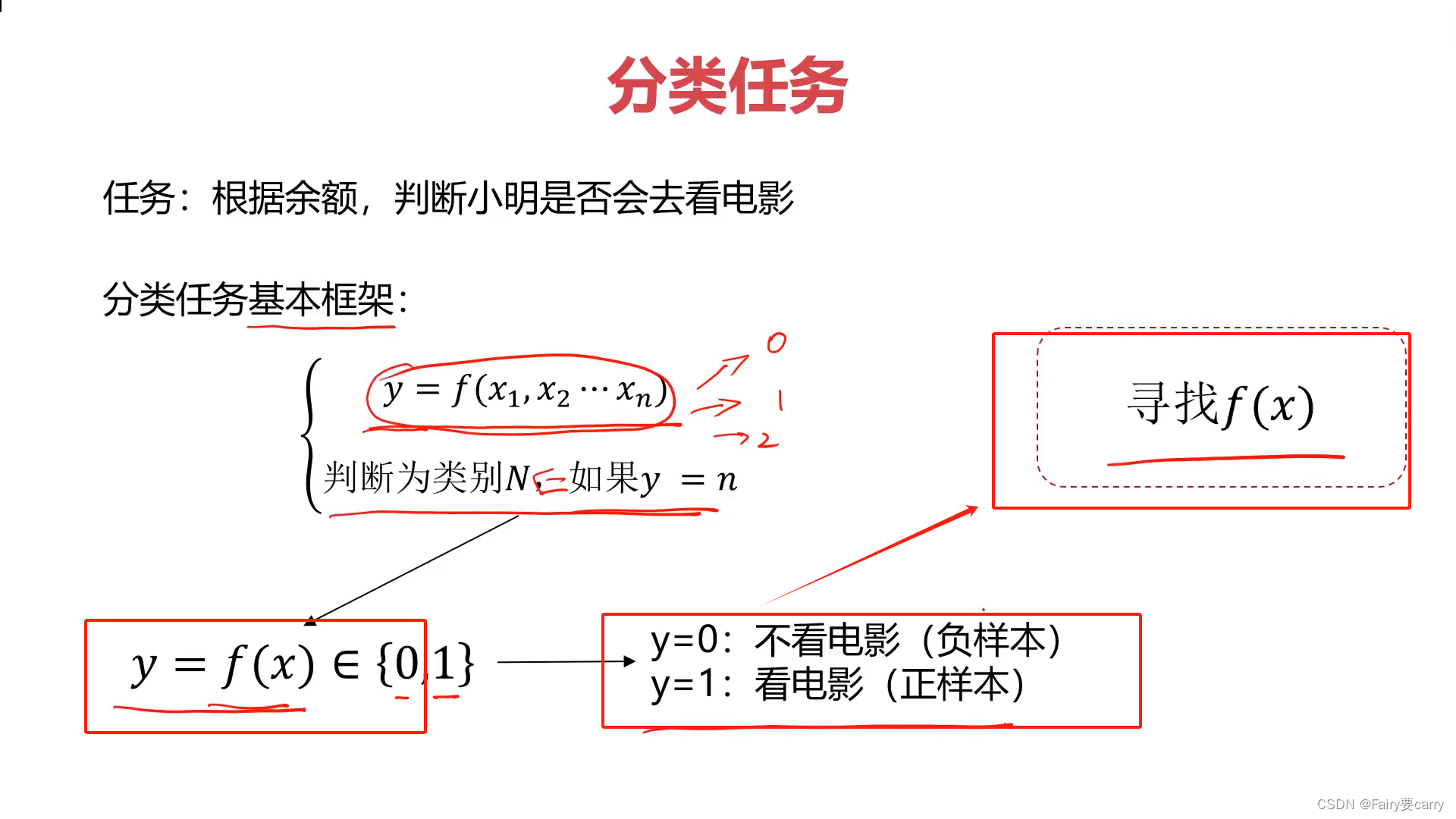
1.什么是分类?
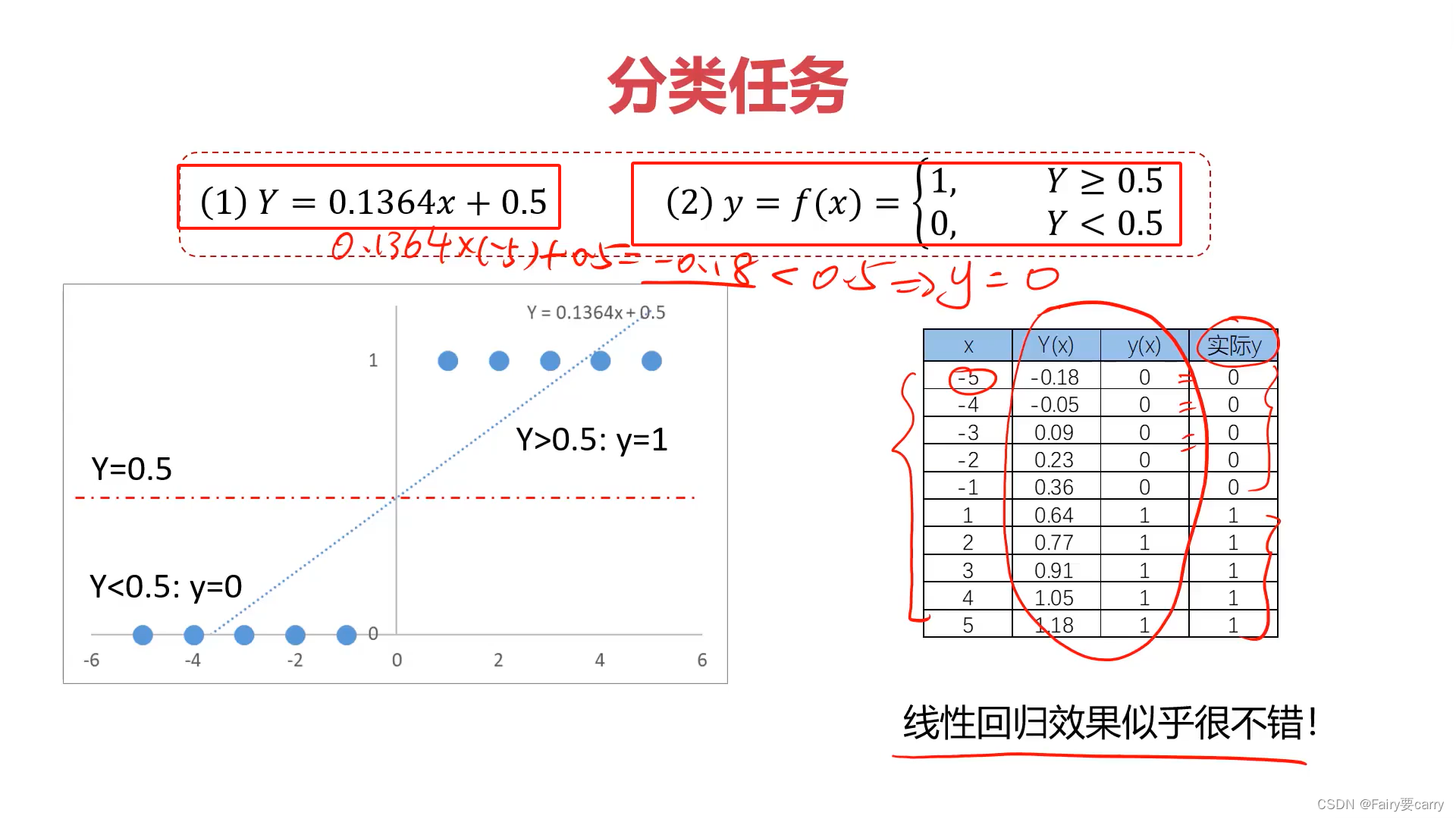
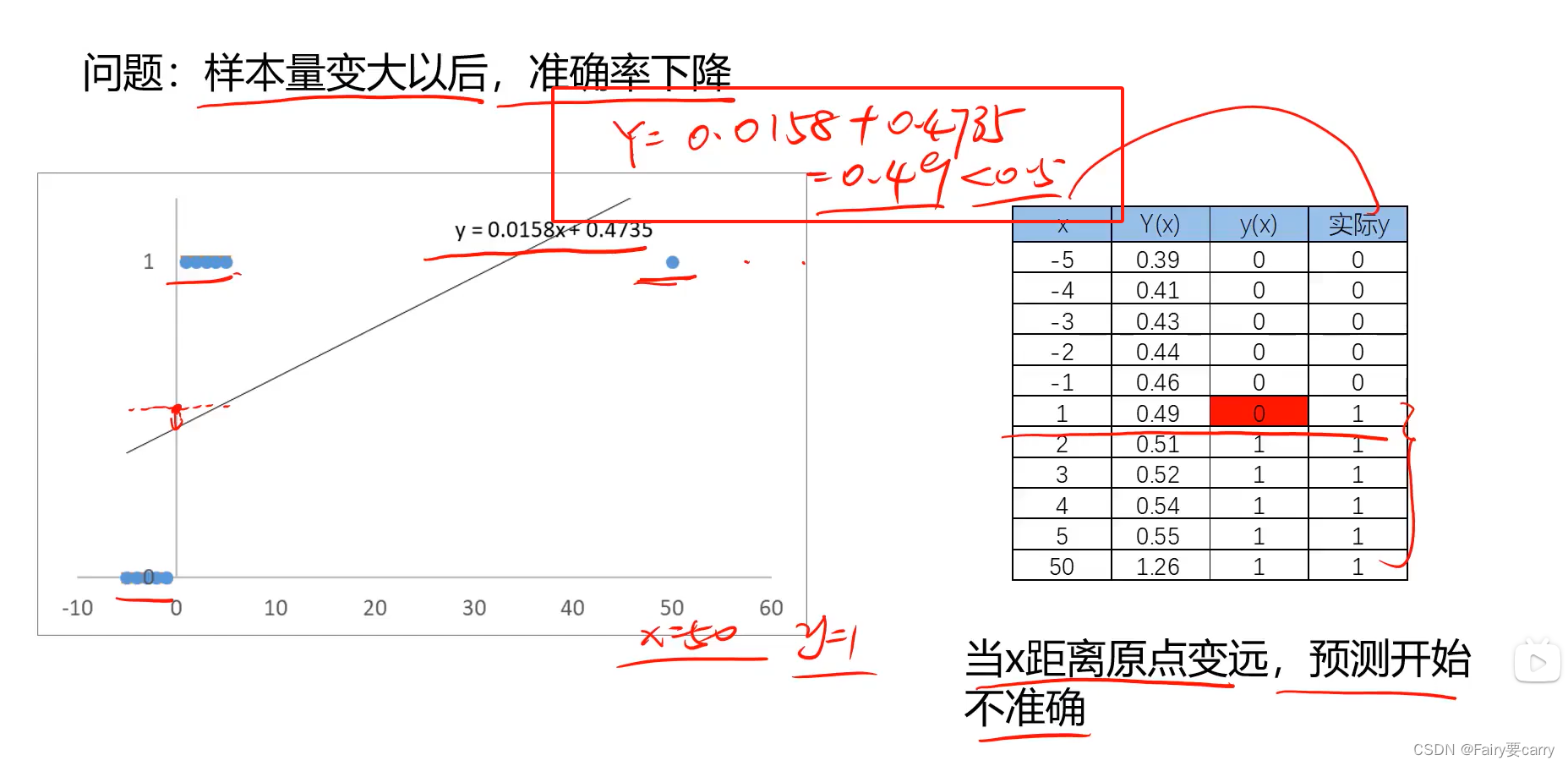
2.局限性:
当样本量逐渐变大的时候,准确率会下降——>因为线性回归曲线距离我们的原点越远,预测就会开始不准确,因为 x前面的倍数就会越来越小,这就导致了样本量变大,但是那些原来靠近原点的点的结果就会可能发生改变;
3.逻辑回归模型
**和线性回归的区别就是:**方程不一样。
**效果:**能够很好地拟合数据,完成分类任务。
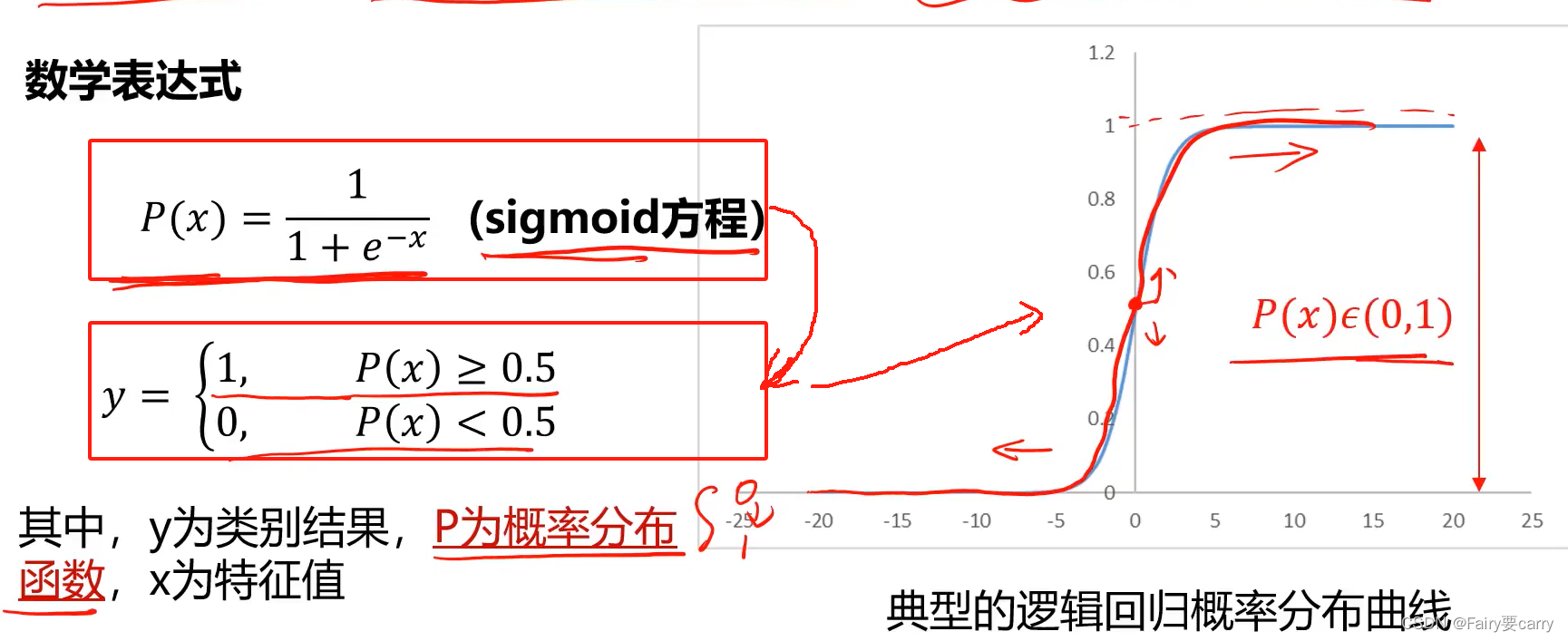
目的:根据数据特征和属性,计算归属于某一类别的概率P(x),根据其概率数值判断其所属类别(应用场景为二分类问题)
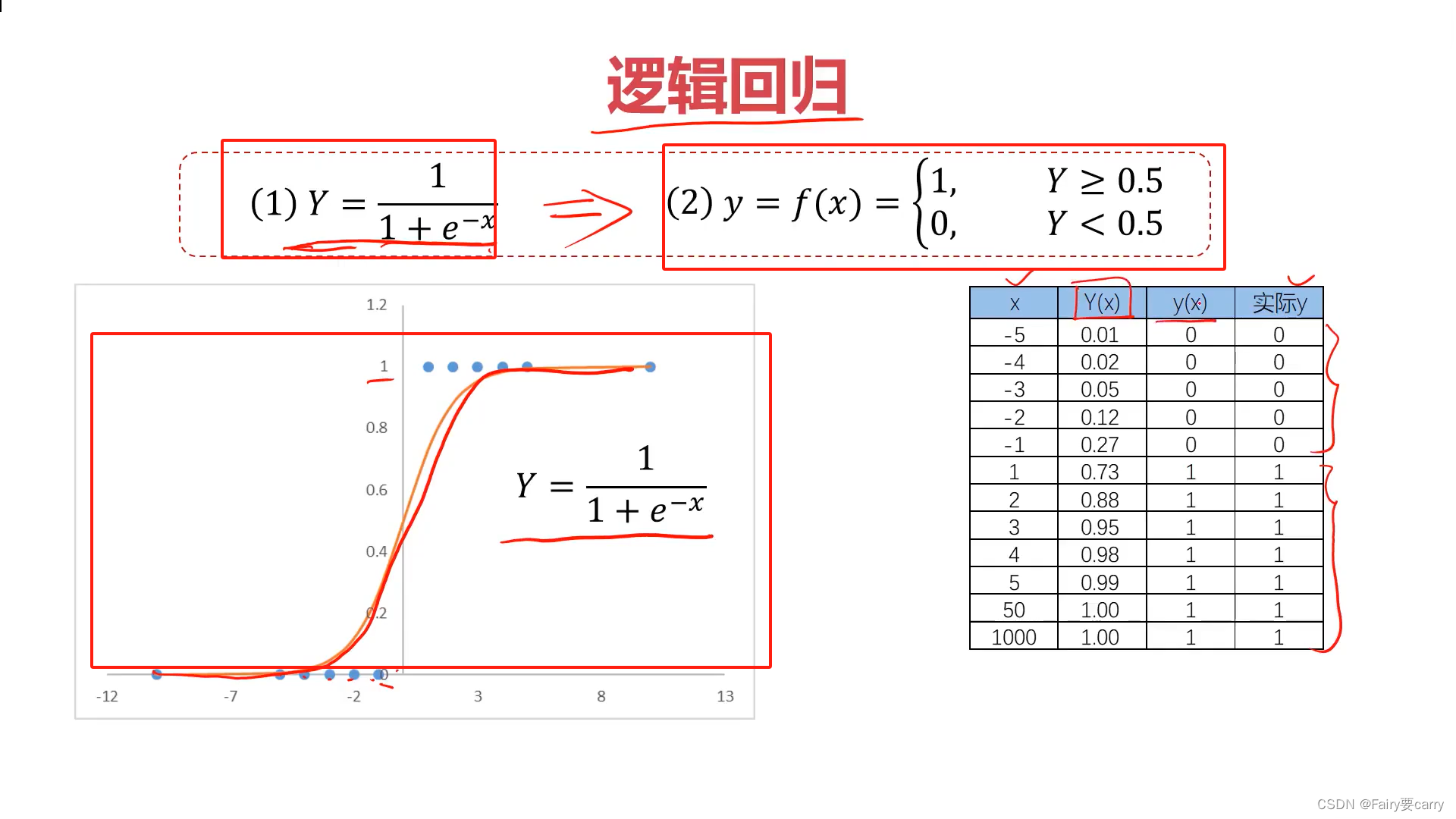
3.1数学表达式:
4. 逻辑回归处理分类任务:
将x=-10和x=100带入P(x)sigmod方程,根据是否大于0.5进行具体判断

5.多因子情况的分类任务考虑:
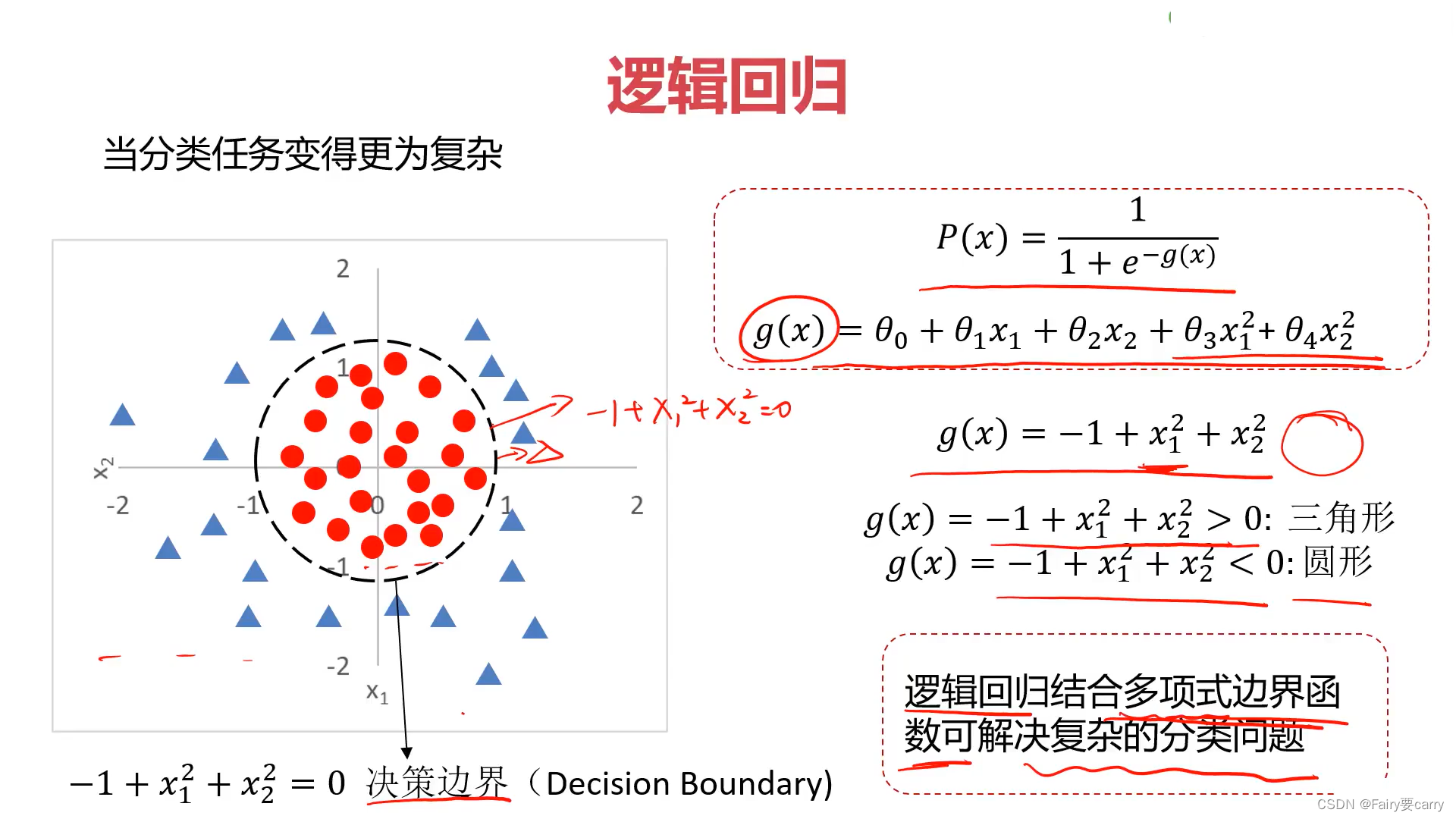
分类任务需要考虑两个最重要的大点,第一点是概率分布函数,第二点是g(x)这个关系函数
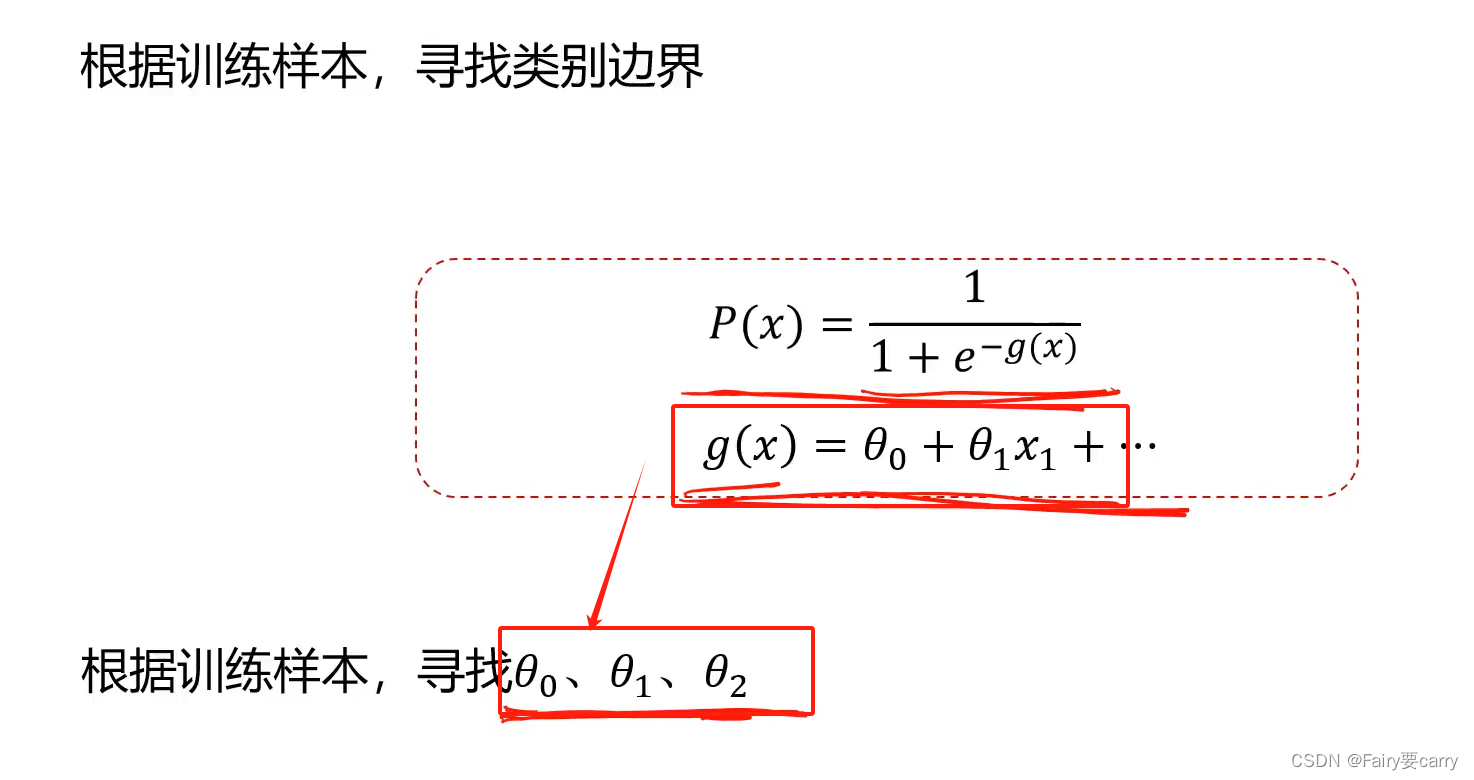
5.1复杂分类任务的求解:
1.首先明确最小损失函数:
我们首先不再使用线性回归方程的损失函数,因为它需要连续的方程而非离散的点,故求不出极小值点,也就是求不出参数
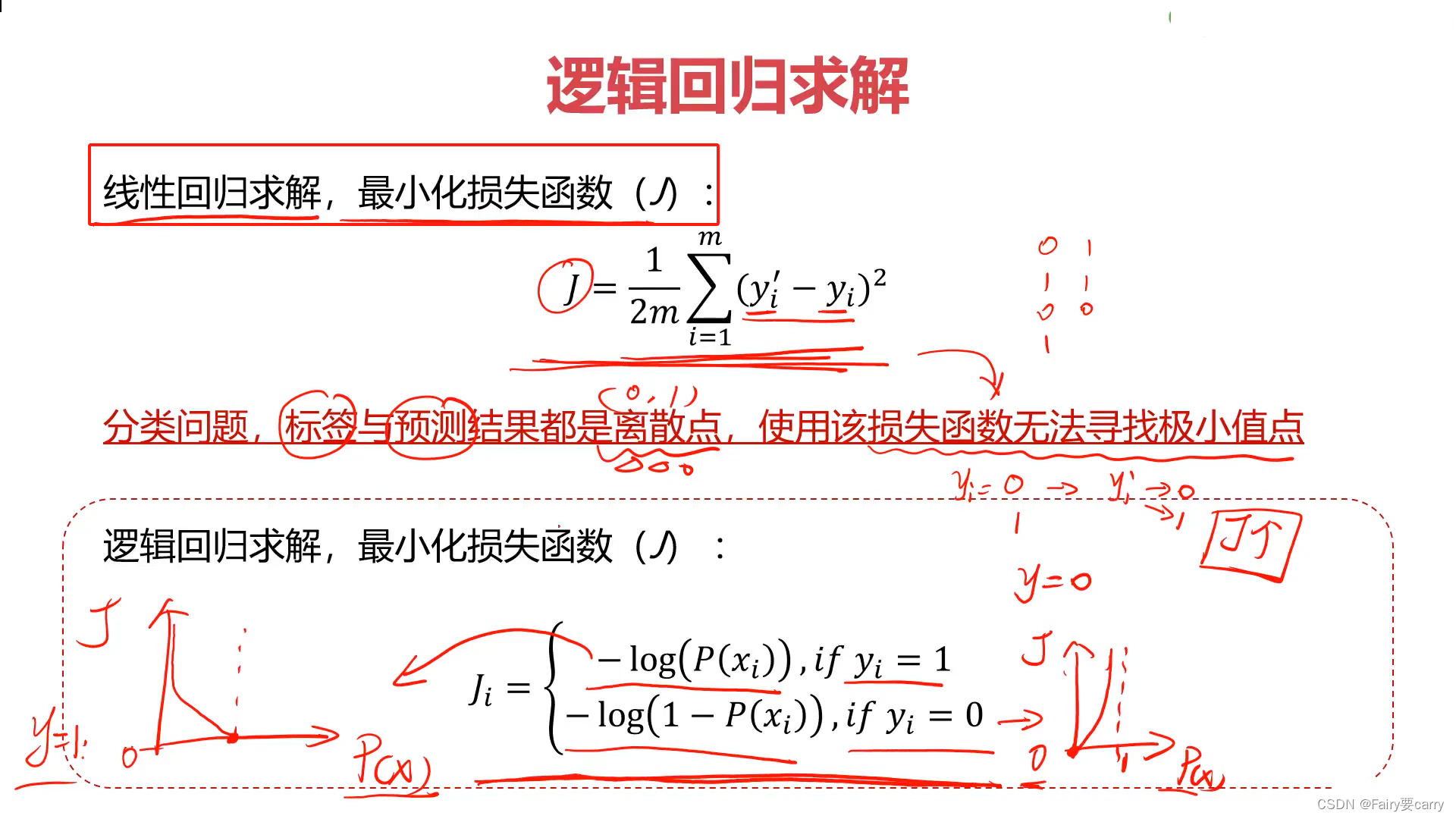
2.整体样本的损失函数J如下所示:
min(J(θ))

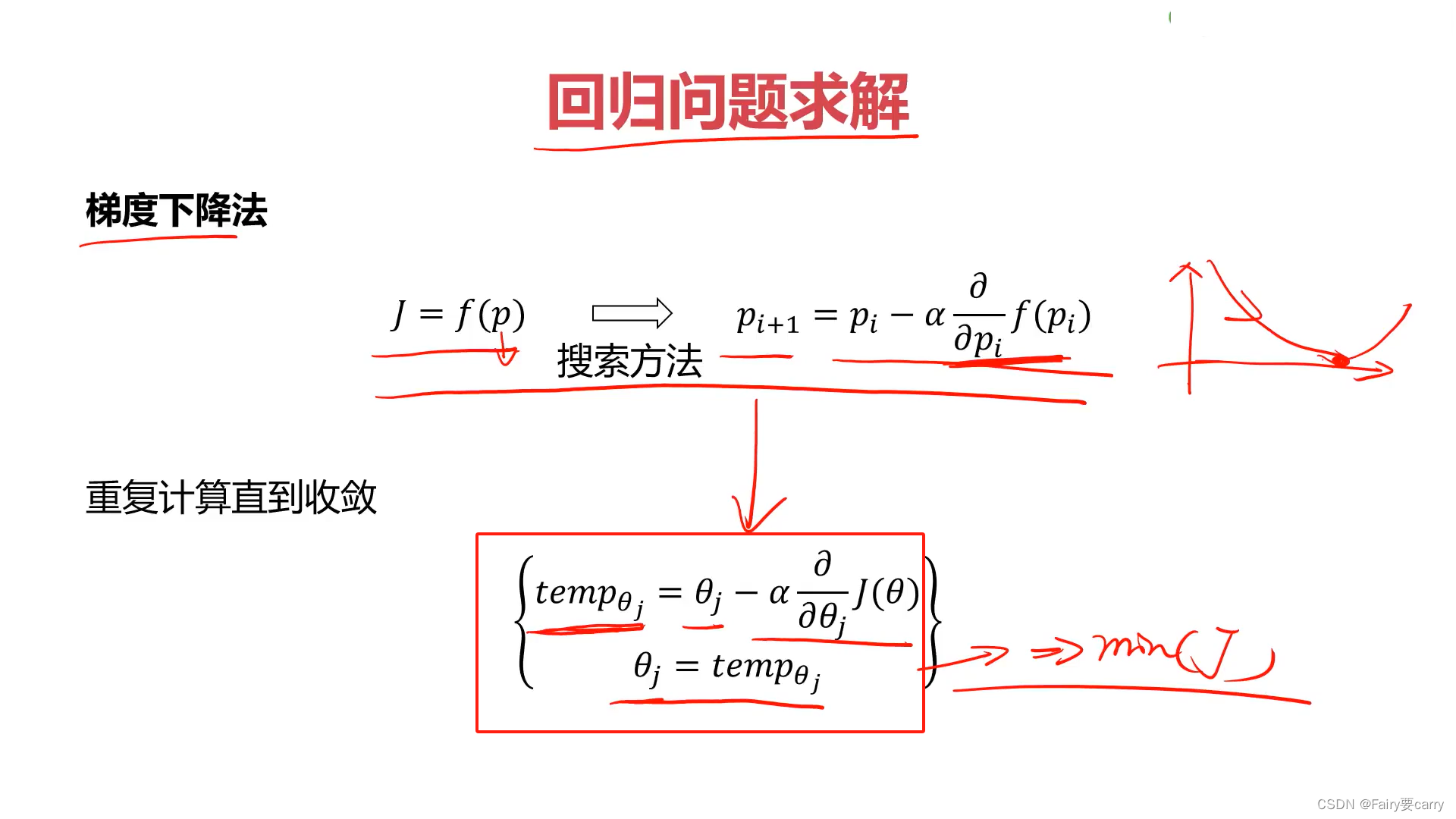
而寻找θ等参数的极值本质还是梯度下降法:
本质:pi+1=pi-αf(pi)对pi求导
迁移:tempθj=θj-αJ(θj)对θj求导
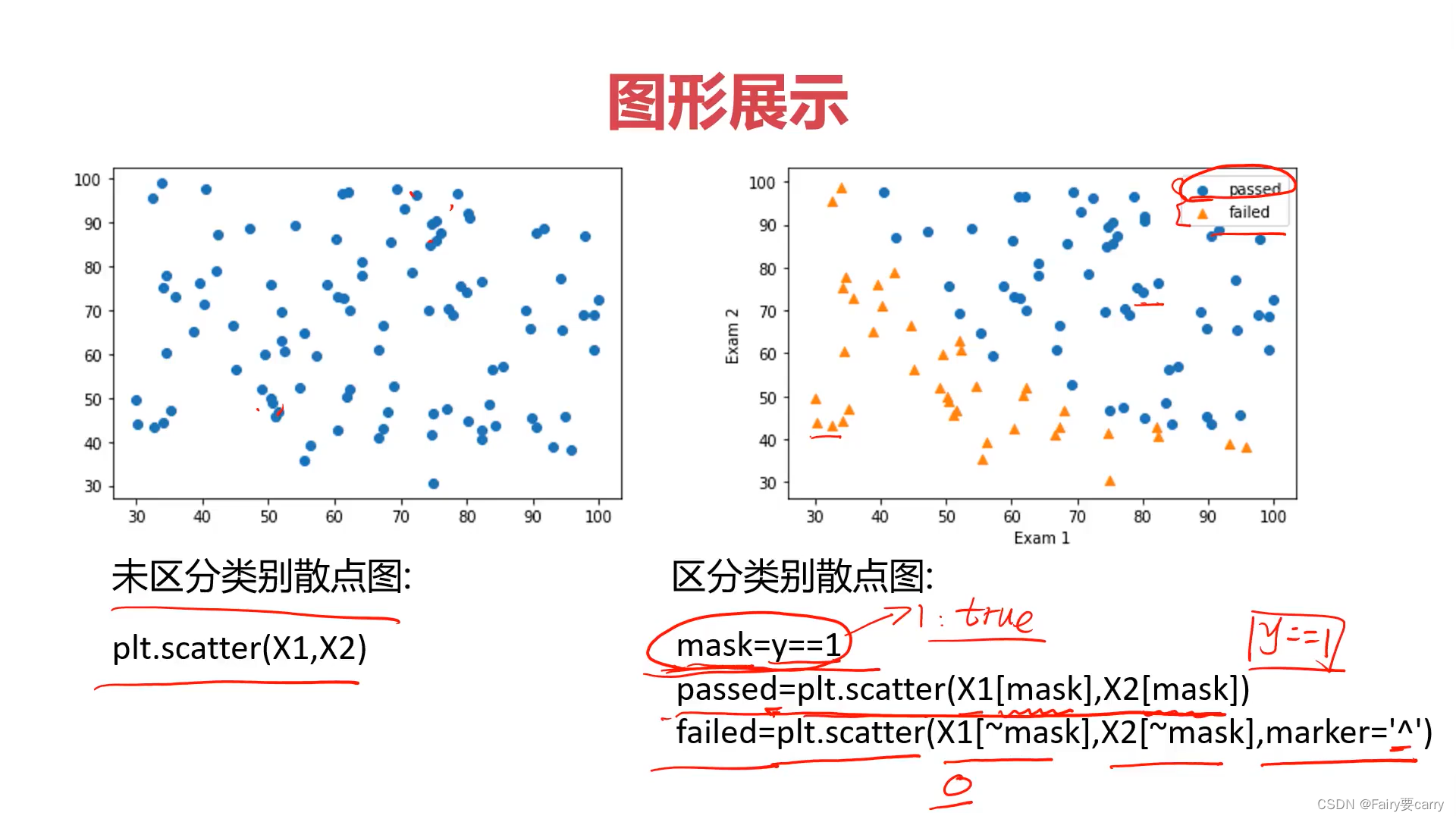
6.区分类散点图:
7.如何利用sklearn得到二分类的边界函数
LogisticRegression:(逻辑回归模型)
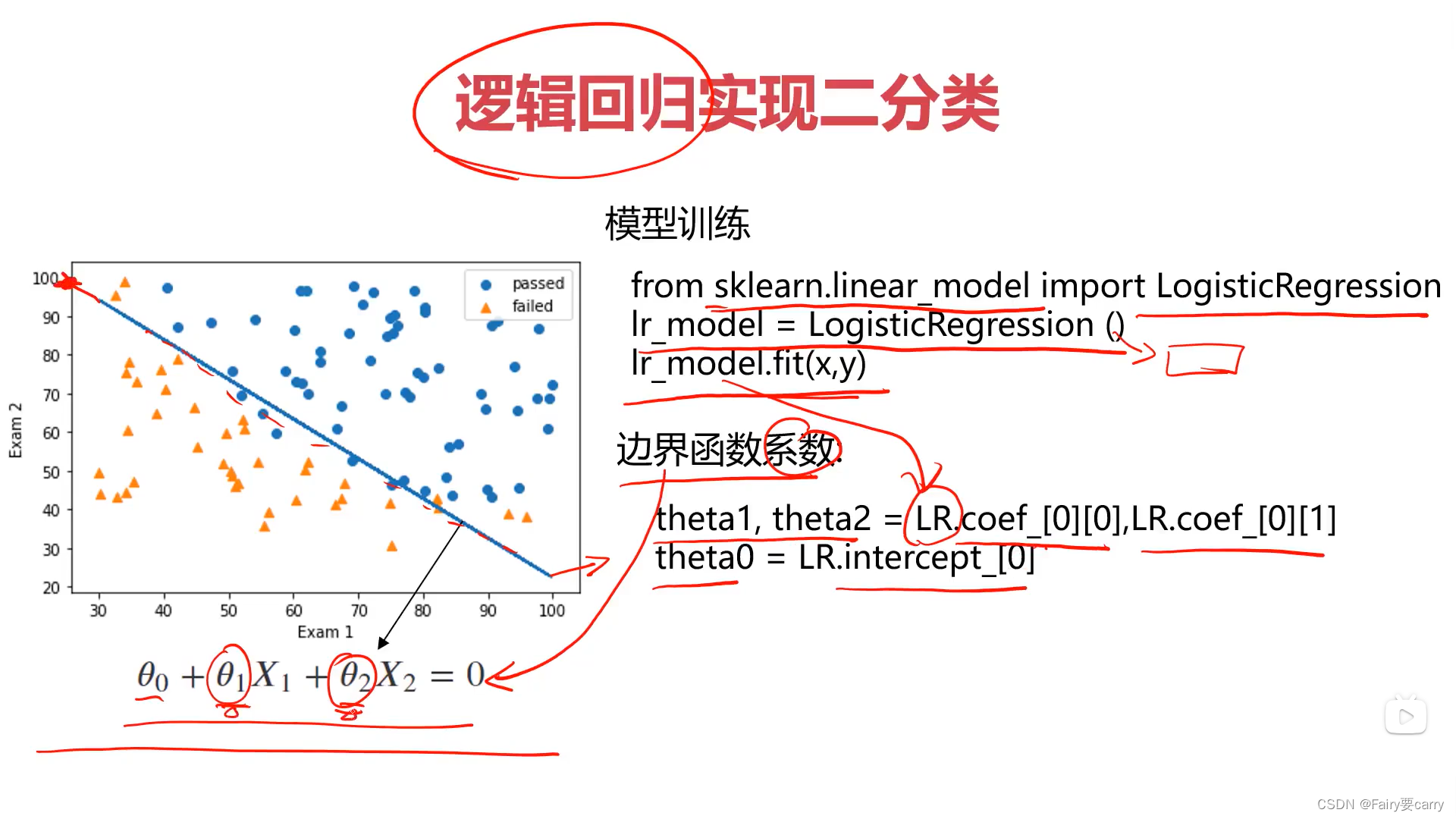
7.1如何优化边界函数得到更加优秀的结果:
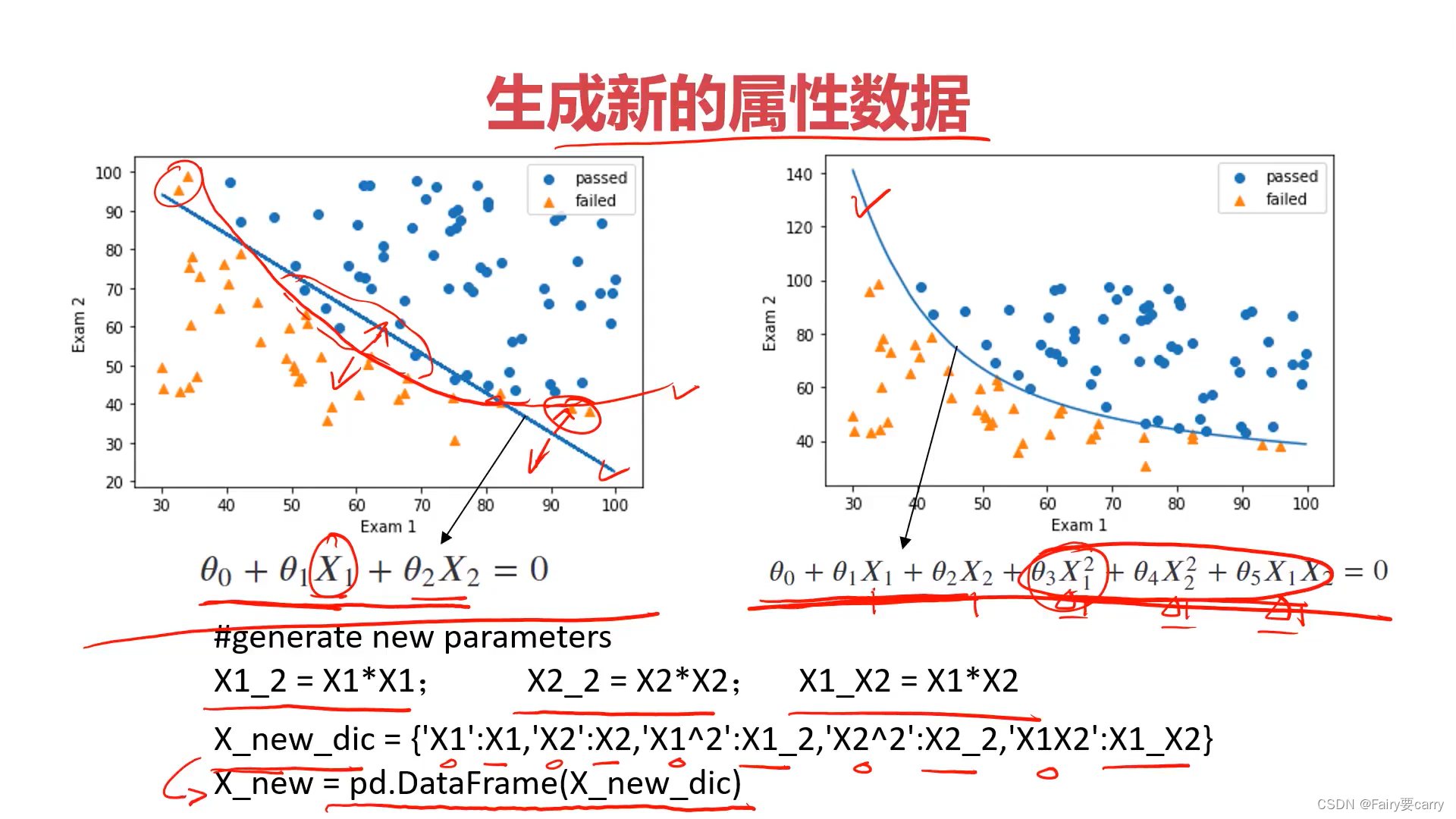
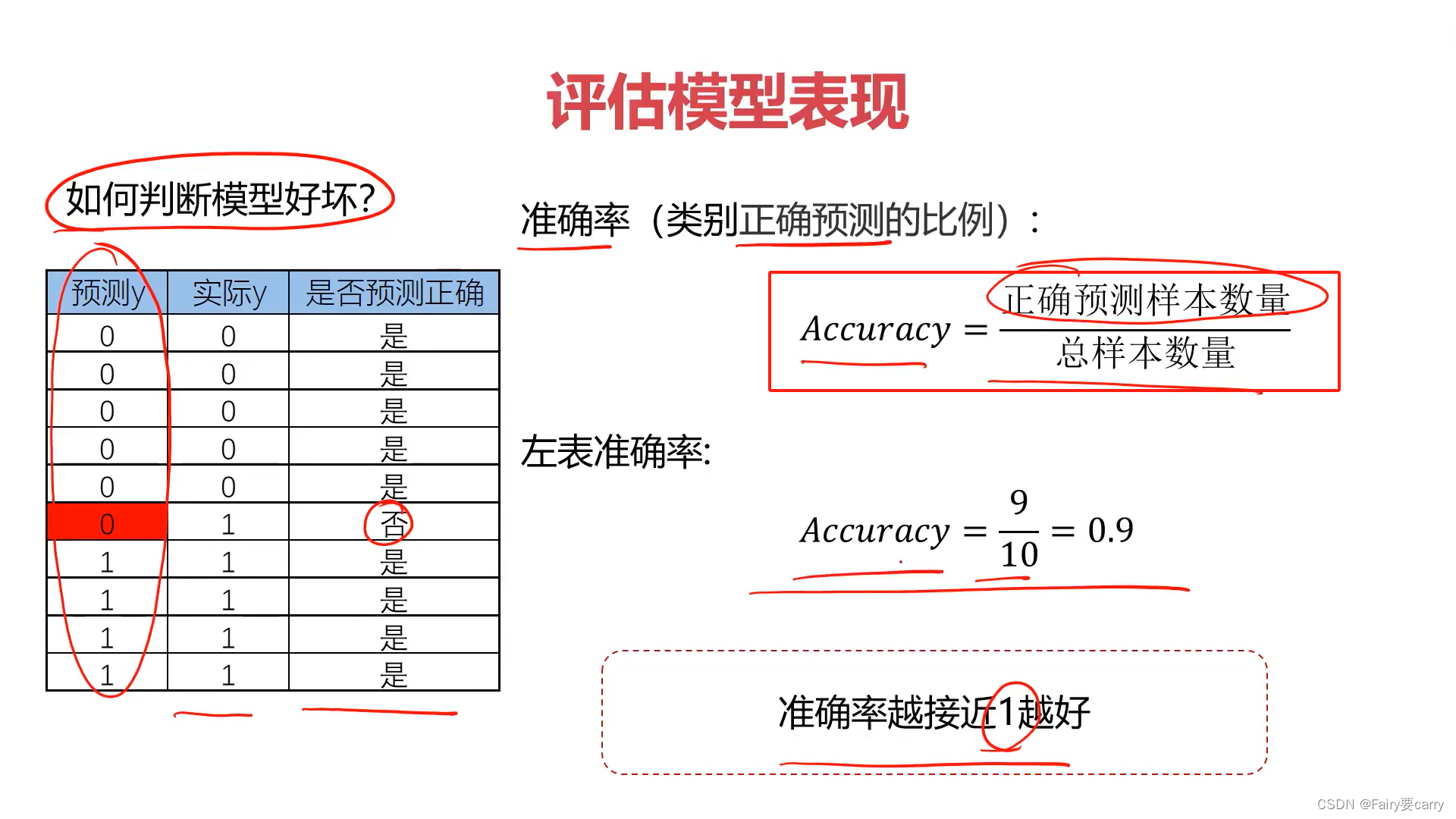
7.2评估模型的表现:
正确样本数量/总样本数量




![[嵌入式系统-72]:RT-Thread-组件:单元测试框架utest](https://img-blog.csdnimg.cn/img_convert/c51e4e0338f75f8cdad9ff75087432e7.jpeg)