【数据结构】------C语言实现二叉树

作者主页：作者主页

数据结构专栏：数据结构

创作时间：2024年5月20日

一、二叉树的定义

二叉树(Binary Tree) 是由n个结点构成的有限集(n≥0)，n=0时为空树，n>0时为非空树。

对于非空树：

有且仅有一个根节点
除根结点外其他可分为两个不相交的子集Tl和Tr，分别称为T TT的左子树和右子树，从定义也可以看出二叉树与一般树的区别主要是两点，一是每个结点的度最多为2；二是结点的子树有左右之分，不能随意调换，调换后又是一棵新的二叉树。

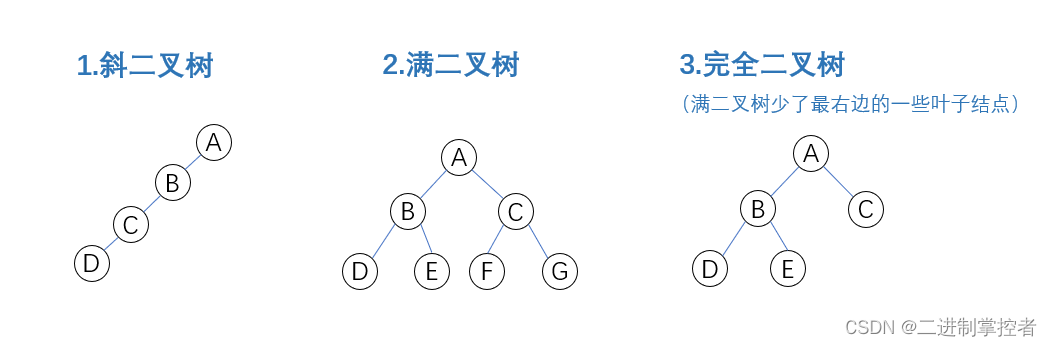
二、二叉树的形态

五种基本形态：

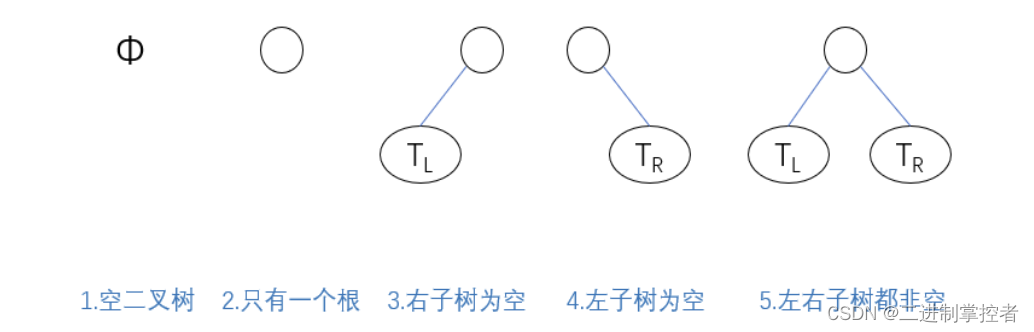
三种特殊形态：

三、二叉树的性质

任意二叉树第 i ii 层最大结点数为2^(i-1)。（i>=1）
深度为 k 的二叉树最大结点总数为2^k-1个（满二叉树）
对于任意二叉树：

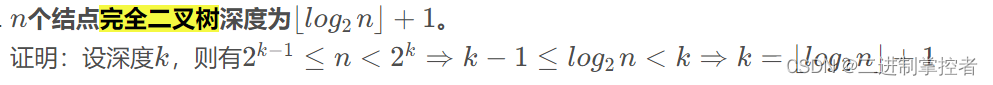
四、二叉树的存储

存的目的是为了取，而取的关键在于如何通过父结点拿到它的左右子结点，不同存储方式围绕的核心也就是这。

顺序存储：

使用一组地址连续的存储单元存储，例如数组。为了在存储结构中能得到父子结点之间的映射关系，二叉树中的结点必须按层次遍历的顺序存放。具体是：

对于完全二叉树，只需要自根结点起从上往下、从左往右依次存储。
对于非完全二叉树，首先将它变换为完全二叉树，空缺位置用某个特殊字符代替（比如#），然后仍按完全二叉树的存储方式存储。

假设将一棵二叉树按此方式存储到数组后，左子结点下标=2倍的父结点下标+1，右子节点下标=2倍的父结点下标+2（这里父子结点间的关系是基于根结点从0开始计算的）。若数组某个位置处值为#，代表此处对应的结点为空。

可以看出顺序存储非常适合存储接近完全二叉树类型的二叉树，对于一般二叉树有很大的空间浪费，所以对于一般二叉树，一般用下面这种链式存储。

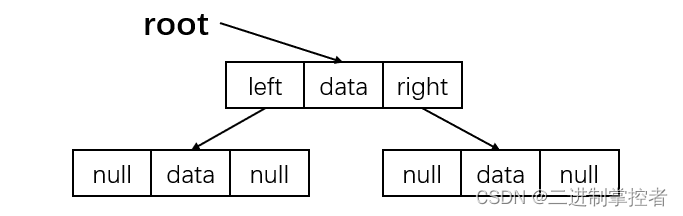
链式存储：

对每个结点，除数据域外再多增加左右两个指针域，分别指向该结点的左孩子和右孩子结点，再用一个头指针指向根结点。对应的存储结构：

二叉树代码的实现：

首先我们要得到相应的自定义函数，然后再去一一实现他们

typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}BTNode;//创建一颗树
BTNode* creatBT();//创建一个新节点
BTNode* BuyNode(int x);//前序遍历
void PrevOrder(BTNode* root);//计算节点个数
int TreeSize(BTNode* root);

由于我们接下来的前序、中序、后序遍历都需要一个二叉树，所以我们这里要先创建一颗二叉树才可以。

创建一个简易二叉树：

//创建一个新节点
BTNode* BuyNode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");exit(0);}newnode->data = x;newnode->left = newnode->right =NULL;return newnode;
}BTNode* creatBT()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

前序遍历：

//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);//输出当前数值PrevOrder(root->left);//然后递归进行PrevOrder(root->right);
}

中序遍历：

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);//先递归，等到最后一个之后再进行输出printf("%d ", root->data);InOrder(root->right);
}

后序遍历：

//后序遍历
void BackOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->data);
}

节点个数：

//节点个数
int treesize(BTNode* root)
{if (root == NULL)return 0;else return treesize(root->left) + treesize(root->right) + 1 ;
}

另一种方式：

int TreeSize(BTNode* root)
{static int size = 0;//用局部静态变量，只初始化一次。if (root == NULL){return 0;}else{++size;}TreeSize(root->left);TreeSize(root->right);return size;
}

求叶子节点个数：

//求叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

树的高度：

int TreeHeigh(BTNode* root)
{if (root == NULL){return 0;}int leftheight = TreeHeigh(root->left);int rightheight = TreeHeigh(root->right);return leftheight > rightheight ?leftheight + 1 : rightheight + 1;
}

总代码：

Tree.h:

#pragma once
#include<iostream>
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}BTNode;//创建一颗树
BTNode* creatBT();//创建一个新节点
BTNode* BuyNode(int x);//前序遍历
void PrevOrder(BTNode* root);//计算节点个数
int TreeSize(BTNode* root);

test.c:

#include"Tree.h"//创建一个新节点
BTNode* BuyNode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");exit(0);}newnode->data = x;newnode->left = newnode->right =NULL;return newnode;
}BTNode* creatBT()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);//输出当前数值PrevOrder(root->left);//然后递归进行PrevOrder(root->right);
}//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);//先递归，等到最后一个之后再进行输出printf("%d ", root->data);InOrder(root->right);
}//后序遍历
void BackOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->data);
}//节点个数
int treesize(BTNode* root)
{if (root == NULL)return 0;else return treesize(root->left) + treesize(root->right) + 1 ;
}int TreeSize(BTNode* root)
{static int size = 0;//用局部静态变量，只初始化一次。if (root == NULL){return 0;}else{++size;}TreeSize(root->left);TreeSize(root->right);return size;
}//求叶子节点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}int TreeHeigh(BTNode* root)
{if (root == NULL){return 0;}int leftheight = TreeHeigh(root->left);int rightheight = TreeHeigh(root->right);return leftheight > rightheight ?leftheight + 1 : rightheight + 1;
}int main()
{BTNode* root = creatBT();InOrder(root);printf("\n");int ret = TreeSize(root);std::cout << "TreeSize:" << ret << std::endl;ret = treesize(root);std::cout << "TreeSize:" << ret << std::endl;ret = TreeLeafSize(root);std::cout << "TreeLeafSize:" << ret << std::endl;int heigh = TreeHeigh(root);std::cout << "TreeHeigh:" << heigh << std::endl;return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/330975.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！