【数学建模】碎纸片的拼接复原

2013高教社杯全国大学生数学建模竞赛B题

问题一
- 模型一
- 模型二
- - 条件设立思路
- 问题求解

问题一

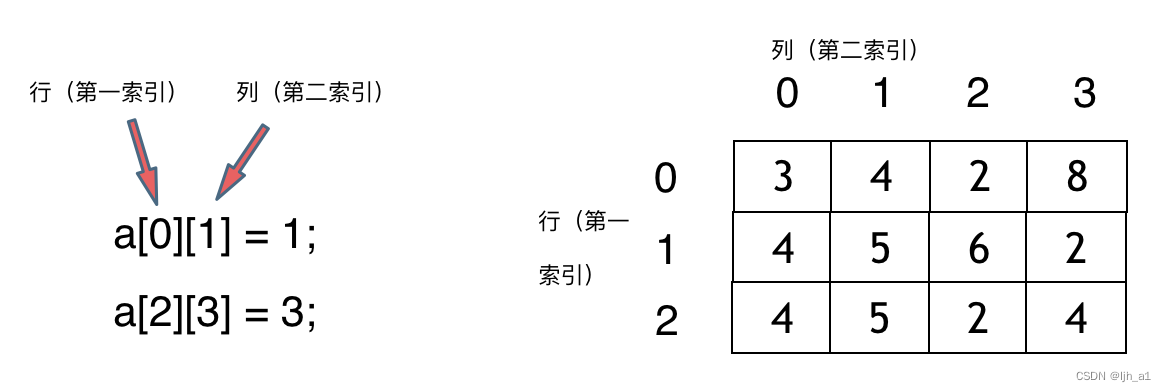
已知 $d_i$ 为第 $i$ 张图片图片的像素矩阵
已知 $d_i$ 都是 $n * m$ 二维矩阵
假设有 $N$ 张图片

模型一

我们认为对应位置像素匹配为
$d_i[j][1]=d_k[j][m]$
那么就有
图片之间匹配度数组
$\displaystyle\sum_{j=1}^m d_i[j][1]=d_k[j][m]$
其中 $A [i] [k]$ 表示第 $i$ 张图片放在第 $k$ 图片后面的匹配度
建立模型:
目标是总匹配度最大
设立0/1变量 $x_{ij}=1$ 表示选择第 $i$ 张在第 $j$ 张后面,并且 $A [i] [j]$ 表示为 $A_{ij}$
已知起始图片为 $a$ ,终止图片为 $b$
$\begin{cases} \max \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=1}^N x_{ij}A_{ij}\\ \displaystyle\sum_{j=1}^N x_{ij} = 1 , i \cancel{=} a , i \cancel{=} j \\ \displaystyle\sum_{i=1}^N x_{ij} = 1 , j \cancel{=} b , j \cancel{=} i \\ i = 1,...,N , j = 1,...,N \end{cases}$

模型二

我们认为对应位置像素匹配不成功的差异为
$d_i[j][1]-d_k[j][m]|$
那么就有
图片之间差异度数组
$\displaystyle\sum_{j=1}^m |d_i[j][1]-d_k[j][m]|$
其中 $A [i] [k]$ 表示第 $k$ 张图片放在第 $i$ 图片后面的差异度
建立模型:
目标是总差异度最小

设立0/1变量 $x_{ij}=1$ 表示选择第 $j$ 张在第 $i$ 张后面,并且 $A [i] [j]$ 表示为 $A_{ij}$
已知起始图片为 $a$ ,终止图片为 $b$
得到目标 $\min \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=1}^N x_{ij}A_{ij}$
要保证除开起始图片，每个图片都有前一张与其对应
$\displaystyle\sum_{i=1}^N x_{ij} = 1 , j \cancel{=} a$
同时除开终止图片也是，要有后一张与其对应
$\displaystyle\sum_{j=1}^N x_{ij} = 1 , i \cancel{=} b$

条件设立思路

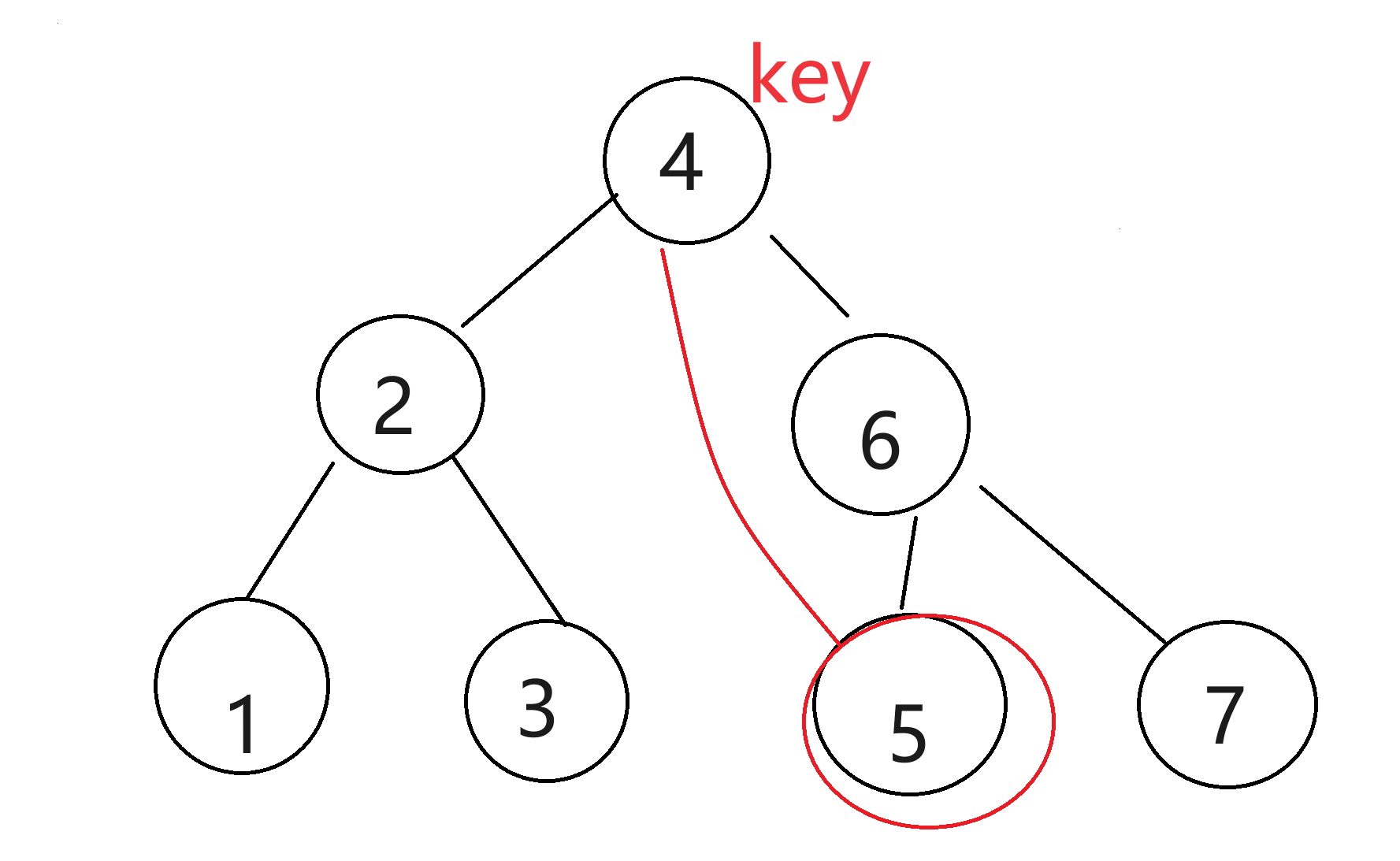
将其看作类似最短路问题
已知起点 $a$ ,终点为 $b$ ，图中每个节点都与其他节点有边，求从起点到终点的最短路问题，并且需要经过每一个节点!

目标依旧不变。
$\min \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=1}^N x_{ij}A_{ij}$
要保证除开起始图片，每个图片都有前一张与其对应，实际上是除开起点，每个节点的入度都为1
$\displaystyle\sum_{i=1}^N x_{ij} = 1 , j \cancel{=} a $
同理除开终点每个节点出度为1
$\displaystyle\sum_{j=1}^N x_{ij} = 1 , i \cancel{=} b$
避开自环存在
$x_{ii} = 0 ,i=1,..,N$
现在唯一的问题就是可能会出现，起点连几个点就到终点，其他点连成环。

目前解决办法，多次运行，如果出现上述情况，手动排除
假设 $3 - > 4 - > 5 - > 6 - > 3$ 成环了
那么 $x_{34}+x_{45}+x_{56}+x_{63}\cancel{=} 4$

所以模型如下:
$\displaystyle\sum_{j=1}^m |d_i[j][1]-d_k[j][m]|$
$\begin{cases} \min \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=1}^N x_{ij}A_{ij}\\ \displaystyle\sum_{i=1}^N x_{ij} = 1 , j \cancel{=} a \\ \displaystyle\sum_{j=1}^N x_{ij} = 1 , i \cancel{=} b \\ i = 1,...,N , j = 1,...,N \end{cases}$

问题求解

数据处理:
MATLAB

d =cell(1,19);
for i = 1:19imageName=strcat(num2str(i-1,'%03d'),'.bmp');d{i}=imread(imageName);
end
a = cell(19,19);
for i = 1:19for j = 1:19sum = 0;for jj = 1:1980sum = sum + abs( double(d{i}(jj,72))-double(d{j}(jj,1)) );% j在i后面的差值enda{i,j} = sum; % 顺序是 i jend
end
xlswrite('D:\homewrok\建模\纸片\201391394826489\2013年全国大学生数学建模竞赛B题附件\附件1\a.xls', a);

lingo

sets:aa/1..19/:;cc(aa,aa):x,d;
endsets
data:a = 9;b = 7;d = @ole('D:\homewrok\建模\纸片\201391394826489\2013年全国大学生数学建模竞赛B题附件\附件1\a.xls','A1:S19');
enddata
min = @sum(cc(i,j):x(i,j)*d(i,j));
@for(aa(i)|(i#ne#b):@sum(aa(j):x(i,j))=1);
@for(aa(j)|(j#ne#a):@sum(aa(i):x(i,j))=1);
@for(cc(i,j)|(i#eq#j):x(i,j)=0);
@for(cc(i,j):@bin(x(i,j)));@for(aa(j):x(b,j)=0);
@for(aa(i):x(i,a)=0);

第一次

                       X( 1, 7)        1.000000            25661.00X( 2, 5)        1.000000            33616.00X( 3, 17)        1.000000            14639.00X( 4, 11)        1.000000            31383.00X( 5, 6)        1.000000            22300.00X( 6, 10)        1.000000            24650.00X( 8, 18)        1.000000            33594.00X( 9, 15)        1.000000            27544.00X( 10, 14)        1.000000            26131.00X( 11, 3)        1.000000            22137.00X( 12, 8)        1.000000            21828.00X( 13, 16)        1.000000            12228.00X( 14, 19)        1.000000            21352.00X( 15, 13)        1.000000            18222.00X( 16, 4)        1.000000            24331.00X( 17, 2)        1.000000            29574.00X( 18, 1)        1.000000            26993.00X( 19, 12)        1.000000            27268.00

发现没有出现上面担心的问题
MATLAB

d =cell(1,19);
for i = 1:19imageName=strcat(num2str(i-1,'%03d'),'.bmp');d{i}=imread(imageName);
end
ansd = [d{9},d{15},d{13},d{16},d{4},d{11},d{3},d{17},d{2},d{5},d{6},d{10},d{14},d{19},d{12},d{8},d{18},d{1},d{7}];
imshow(ansd);

在这里插入图片描述

同理做附件二:

d =cell(1,19);
for i = 1:19imageName=strcat(num2str(i-1,'%03d'),'.bmp');d{i}=imread(imageName);
end
ansd = [d{4},d{7},d{3},d{8},d{16},d{19},d{12},d{1},d{6},d{2},d{10},d{14},d{11},d{9},d{13},d{15},d{18},d{17},d{5}];
imshow(ansd);