【数据结构】AVL树——平衡二叉搜索树

个人主页：东洛的克莱斯韦克-CSDN博客

祝福语：愿你拥抱自由的风

二叉搜索树

AVL树概述

平衡因子

旋转情况分类

左单旋

右单旋

左右双旋

右左双旋

AVL树节点设计

AVL树设计

详解单旋

左单旋

右单旋

详解双旋

左右双旋

平衡因子情况如下

右左双旋

平衡因子情况如下

二叉搜索树

【C++】详解二叉搜索树-CSDN博客

AVL树概述

平衡树：左子树的高度等于右子树的高度

不平衡树：左子树的高度不等于等于右子树的高度

二叉搜索树很难是一颗平衡树。

对二叉树进行插入和删除的操作，或插入大量的数据不够随机，都会是使二叉搜索树不够平衡。

极端情况下，二叉树会退化成类似链表的结构，那么二叉搜索树查询数据的效率荡然无存。

在二叉树的基础上加入平衡的概念就是平衡二叉搜索树，也叫AVL树。

AVL树也不是一颗绝对的平衡树，AVL树的平衡是相对的，它允许左子树和右子树的高度为 1 ，但不能超过 1 。

平衡是相对的很好理解，因为一个父亲节点最多只能有两个孩子节点，而数据又是一个一个插入的，所以一定会出现左子树和右子树高度差为 1 的情况。

B树可达到绝对平衡，因为B树是多叉结构——一个父亲节点有多个孩子节点

如果左子树和右子树的高度差为 2 ，就视为打破平衡。

如果打破平衡，就需要通过旋转这一操作让左右子树的高度差小于等于 1 。

AVL树是保持一种相对平衡的状态，而不是绝对平衡。那么AVL树搜索数据的效率只能是接近 $O(logN)$ 。

AVL树只是保证了搜索效率的下限，而不是提高了上限

平衡因子

平衡因子这一概念并不是AVL树所必备的——从代码实现的角度来说，如果不加入平衡因子的概念理解起来会比较抽象。

平衡因子：让每个节点存一个整型，该整形值的大小等于右子树的高度减左子树的高度

平衡因子等于 0 ：左右子树平衡

平衡因子等于 1 ：左右子树相对平衡，右树偏高

平衡因子等于 -1 ：左右子树相对平衡，左树树偏高

平衡因子等于 2 或 -2 ：左右子树不平衡

平衡因子的更新：

插入父亲节点的右边平衡因子加加，插入父亲节点的右边平衡因子减减，

父亲节点更新后的平衡因子等于 1 或 -1 ，需要不断往上（溯源）更新，直到父亲节点的平衡因子为 0 或更新至整棵树的根节点就停止更新。

如果父亲节点的平衡因子为 2 或 -2 时，需要对这棵子树旋转，旋转后更新平衡因子

示例

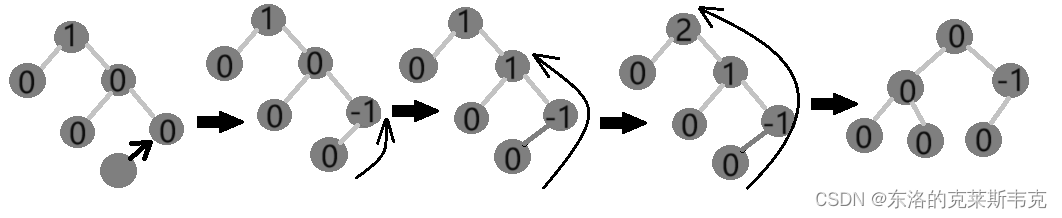
旋转情况分类

旋转分为：

左单旋 右单旋 左右双旋 右左双旋

左单旋

：新节点插入较高右子树的右侧

具象图：

抽象图：

那么左单旋是怎么旋的呢？核心步骤为：

设父亲节点为：fathernode 孩子节点为：cur

让cur的左孩子成为fathernode的右孩子，

再让fathernode成为cur的左孩子。

如下示意图

右单旋

：新节点插入较高左子树的左侧

具象图：

抽象图：

那么右单旋是怎么旋的呢？核心步骤为：

设父亲节点为：fathernode 孩子节点为：cur

让cur的右孩子成为fathernode的左孩子，

再让fathernode成为cur的右孩子

如下示意图：

左右双旋

：新节点插入在较高左子树的右侧——先左单旋再右单旋

左右双旋的核心步骤为：

设父亲节点为：fathernode

父亲的左孩子节点为：fathernodeL

父亲的左孩子节点的右孩子节点的为fathernodeLR

先让fathernodeL左单旋，再让fathernodeLR进行右单旋

这里小编直接上抽象图：

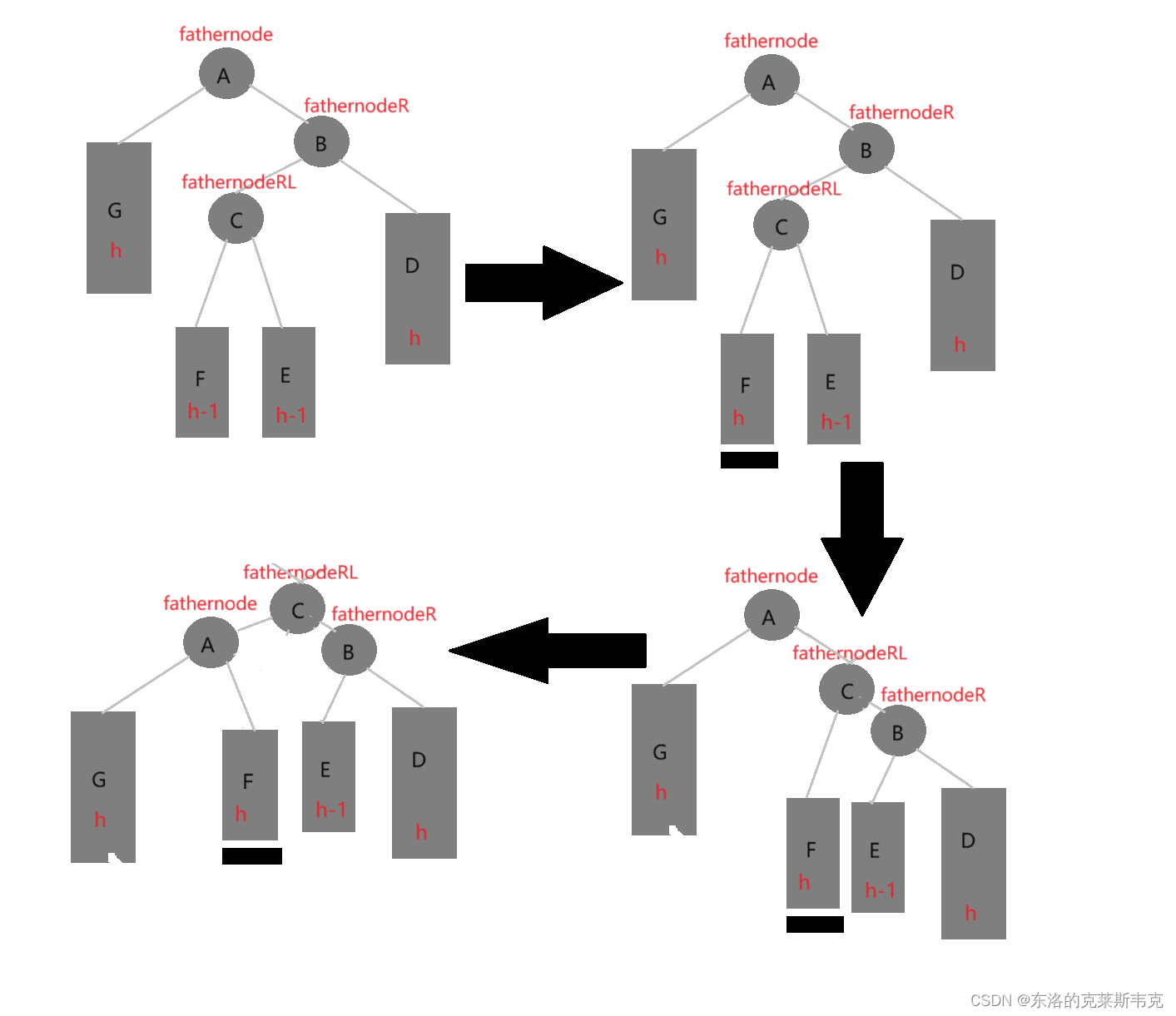
右左双旋

：新节点插入再较高右子树的左侧——先右单旋再左单旋

设父亲节点为：fathernode

父亲的右孩子节点为：fathernodeR

父亲的右孩子节点的左孩子节点的为fathernodeRL

先对fathernodeR进行右单旋，再对fathernode进行左单旋。

示意图：

AVL树节点设计

【C++】详解C++的模板-CSDN博客

AVL树的节点需要三个指针，分别指向左孩子节点，右孩子节点，父亲节点。指向父亲节点的指针是为了能溯源更新平衡因子。

需要一个整型存储平衡因子，平衡因子在构造函数的初始化列表中初始化为 0，因为新节点左右孩子都为空。

template <class K>
class AVLTreeNode
{
public:AVLTreeNode(const K& key) //构造函数:_key(key), _left(nullptr), _right(nullptr), _FatherNode(nullptr), _bf(0){}K _key; //键值   AVLTreeNode<K>* _left;//左孩子AVLTreeNode<K>* _right;//右孩子AVLTreeNode<K>* _FatherNode;//父亲  int _bf;//平衡因子};

AVL树设计

template <class K>
class AVLTree
{typedef AVLTreeNode<K> node; node* _root;public:AVLTree()  //构造函数，初始化为空树:_root(nullptr){}bool Insert(const K& key)//插入元素{
//if (nullptr == _root) //是否是空树{_root = new node(key);  return true;}
//node* cur = _root;node* fathernode = nullptr;while (cur)  //查找插入的位置，如果树中已经有要插入的值，则插入失败，{if (cur->_key < key){fathernode = cur;cur = cur->_right;}else if (cur->_key > key){fathernode = cur;cur = cur->_left;}else{return false;}}cur = new node(key); //新插入节点 if (fathernode->_key < cur->_key) //判断新节点应该是左孩子还是右孩子{fathernode->_right = cur;cur->_FatherNode = fathernode;}else{fathernode->_left = cur;cur->_FatherNode = fathernode;}//while (fathernode)//更新平衡因子{if (cur == fathernode->_left){fathernode->_bf--;}else  if (cur == fathernode->_right){fathernode->_bf++;}//if (fathernode->_bf == 0){// 更新结束break;}else if (fathernode->_bf == 1 || fathernode->_bf == -1){// 继续往上更新cur = fathernode;fathernode = fathernode->_FatherNode;}else if (fathernode->_bf == 2 || fathernode->_bf == -2){// 子树不平衡了，需要旋转if (fathernode->_bf == 2 && cur->_bf == 1){RevolveLeft(fathernode);//左单旋}else if (fathernode->_bf == -2 && cur->_bf == -1){RevolveRight(fathernode);//右单旋}else if (fathernode->_bf == 2 && cur->_bf == -1){RevolveRightLeft(fathernode); //右左双旋   }else if (fathernode->_bf == -2 && cur->_bf == 1){RevolveLeftRight(fathernode);//左右双旋}else{assert(false);   //平衡因子出问题了}break;}}return true;}}

下面通过代码的细节来深入理解旋转

详解单旋

左单旋

完整代码如下

void RevolveLeft(node *& fathernode)//左单旋      
{node* cur = fathernode->_right; //父亲节点的右孩子fathernode->_right = cur->_left; //更改指向关系if (cur->_left != nullptr) //特殊情况cur->_left->_FatherNode = fathernode;//更改指向关系cur->_FatherNode = fathernode->_FatherNode;//更改指向关系if (fathernode->_FatherNode != nullptr) //为空是特殊情况，{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更改指向关系}else{fathernode->_FatherNode->_left = cur;//更改指向关系}}cur->_left = fathernode;//更改指向关系fathernode->_FatherNode = cur;//更改指向关系fathernode->_bf = 0; //更新平衡因子cur->_bf = 0;}

处理指向关系时，一定不要忘了更改父亲的指向关系

经过左单旋之后，父亲节点和右孩子节点的平衡因子都为 0 ，可参考上文图示。

特殊情况如下，如果不处理特殊情况，程序很容易崩溃

右单旋

void RevolveRight(node *& fathernode) //右单旋
{node* cur = fathernode->_left; //父亲节点的左节点fathernode->_left = cur->_right;//更新指向关系if (cur->_right != nullptr) //特殊情况cur->_right->_FatherNode = fathernode;//更新指向关系cur->_FatherNode = fathernode->_FatherNode;//更新指向关系if (fathernode->_FatherNode != nullptr)//特殊情况{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更新指向关系}else{fathernode->_FatherNode->_left = cur;//更新指向关系}}cur->_right = fathernode;//更新指向关系fathernode->_FatherNode = cur;//更新指向关系fathernode->_bf = 0;//更新平衡因子cur->_bf = 0;
}

详解双旋

左右双旋

左右双旋只需复用左单旋和右单旋即可，但平衡因子的更新却比较麻烦。

完整代码如下

	void RevolveLeftRight(node *& fathernode)//左右双旋    {node* fathernodeL = fathernode->_left; //父亲节点的左孩子节点node* fathernodeLR = fathernodeL->_right;//父亲节点的左孩子节点的右孩子节点int bf = fathernodeLR->_bf; //保存平衡因子，实际是为了判断是插入了fathernodeLR左边还是右边还是fathernodeLR本身插入RevolveLeft(fathernodeL);RevolveRight(fathernode);//更新平衡因子if (bf == 0){fathernode->_bf = 0;fathernodeL->_bf = 0;fathernodeLR->_bf = 0;}else if (bf == -1){fathernode->_bf = 1;fathernodeL->_bf = 0;fathernodeLR->_bf = 0;}else if (bf == 1){fathernodeL->_bf = -1;fathernode = 0;fathernodeLR = 0;}else{assert(false);}}

平衡因子情况如下

右左双旋

完整代码如下

	void RevolveRightLeft(node *& fathernode) //右左双旋 {node* fathernodeR = fathernode->_right; node* fathernodeRL = fathernodeR->_left;int bf = fathernodeRL->_bf;RevolveRight(fathernodeR);RevolveLeft(fathernode);if (bf == 0){fathernode->_bf = 0;fathernodeR->_bf = 0;fathernodeRL->_bf = 0;}else if (bf == 1){fathernode->_bf = -1;fathernodeR->_bf = 0;fathernodeRL->_bf = 0;}else if (bf == -1){fathernodeR->_bf = 1;fathernode->_bf = 0;fathernodeRL->_bf = 0;}else{assert(false); }}