柱状图中最大的矩形

题目

分析

矩形的面积等于宽乘以高，因此只要能确定每个矩形的宽和高，就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始，到下标为 j 的柱子结束，那么这两根柱子之间的矩形（含两端的柱子）的宽是 j-i+1，矩形的高就是两根柱子之间的所有柱子最矮的高度。

暴力解法（不可取）

        如果能逐一找出直方图中所有矩形并比较它们的面积，就能够得到最大矩形的面积。方法为：采用嵌套的二重循环遍历所有矩形，并比较他们的面积。该种方法的时间复杂度为O(N^2)，根据题目所给的提示可知，这种方法不能解决本题，会超时。

代码为

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};

分治法（本题不可取）

        仔细观察直方图可以发现，这个直方图的最大矩形有3中可能：

第一种：矩形通过直方图中最矮的柱子；

第二种：矩形的起始柱子和终止柱子都在直方图中最矮柱子的左侧；

第三种：矩形的起始柱子和终止柱子都在直方图中最矮柱子的右侧。

第二种和第三种从本质上来说和求整个直方图的最大矩形面积是同一个问题，可以用递归函数解决。

代码为：

class Solution {
public:int largestRectangleArea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};

单调栈法（可取）

        下面介绍一种非常高效，巧妙的解法。这种解法用一个栈保存直方图的柱子，并且在栈中的柱子的高度是递增排序的。为了方便计算矩阵的高度，栈中保存的是柱子在数组中的下标，可以根据下标得到柱子的高度。

        这种解法的基本思想是确保保存在栈中的直方图的柱子的敢赌是递增排序的。假设从左到右逐一扫描数组中的每根柱子，如果当前柱子的高度大于位于栈顶柱子的高度，那么将该柱子的下标入栈；否则，将位于栈顶的柱子的下标出栈，并且计算以位于栈顶的柱子为顶的最大矩形的面积。【注意：此时出栈须满足：栈不为空并且栈顶柱子的高度大于等于当前柱子的高度】

        以某根柱子为顶的最大矩形，一定是从该柱子向两侧眼神知道遇到比它矮的柱子，这个最大矩形的高是该柱子的高，最大矩形的宽是两侧比它矮的柱子中间的间隔。

        如果当前扫描到的柱子的高小于位于栈顶柱子的高，那么将位于栈顶的柱子的下标出栈，并且计算以位于栈顶的柱子为顶的最大矩形的面积。由于保存在栈中的柱子的高度是递增排序的，因此栈中位于栈顶前面的一根柱子一定比位于栈顶的柱子矮，于是很容易就能找到位于栈顶的柱子两侧比它矮的柱子。

        当计算以当前柱子为顶的最大矩形的面积时，如果栈中没有柱子，那么意味着它左侧的柱子都比它高，因此可以想象在下标为 -1 的位置有一根比它矮的柱子。

        当扫描数组中所以柱子之后，栈中可能仍然剩余一些柱子。因此，需要注意将这些柱子的下标出栈并计算以它们为顶的最大矩形的面积。

        在扫描完数组中所有的柱子之后，当计算以当前柱子为顶的最大矩形的面积时，说明它的右侧没有比它矮的柱子，如果一根柱子的右侧有比它矮的柱子，那么当扫描到右侧较矮柱子的时候他就已经出栈了。因此，可以想象下标为数组长度的位置有一根比它矮的柱子。

        由于已经计算了以每根柱子为顶的最大矩形面积，因此比较这些矩形的面积就能得到脂肪图中的最大矩形面积。

代码为

class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();stack<int> st;st.push(-1);int maxarea=0;for(int i=0;i<n;i++){while(st.top()!=-1 && heights[st.top()]>=heights[i]){int height=heights[st.top()];st.pop();int width=i-st.top()-1;maxarea=max(maxarea,height*width);}st.push(i);}while(st.top() != -1){int height=heights[st.top()];st.pop();int width=n-st.top()-1;maxarea=max(maxarea,height*width);}return maxarea;}
};

最大矩形

题目

分析

        上一道题是关于最大矩形的，这道题也是关于最大矩形的，他们之间有没有某种联系？如果能从矩阵中找出直方图，那么就能通过计算直方图中的最大矩形面积来计算矩阵中的最大矩形面积。

        直方图是由排列在同一基线上的相邻柱子组成的图形，由于题目要求矩形中只包含数字1，因此将矩阵中上下相邻的值为1的各自看成直方图中的柱子，如果分别以矩阵的每行为基线，就可以得到若干行由数字1的格子组成的直方图。如下图所示：

对应的直方图如下：

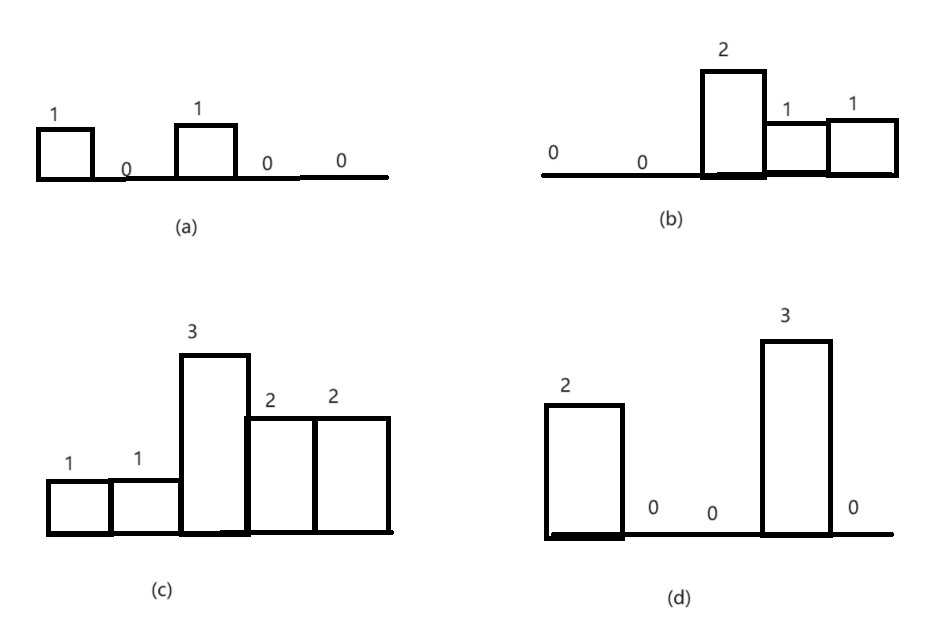
说明：（a）以矩阵第一行为基线的直方图；（b）以矩阵第二行为基线的直方图；（c）以矩阵第三行为基线的直方图；（d）以矩阵第四行为基线的资方图。

暴力解法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};

分治法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};

单调栈法（可取）

class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int> v){stack<int> st;st.push(-1);int area=0;for(int i=0;i<v.size();i++){while(st.top()!=-1 && v[i]<=v[st.top()]){int height=v[st.top()];st.pop();int width=i-st.top()-1;area=max(area,height*width);}st.push(i);}while(st.top()!=-1){int height=v[st.top()];st.pop();int width=v.size()-st.top()-1;area=max(area,height*width);}return area;}
};